ホイートストンブリッジ回路（検流計に電流が流れる向き）

PHYさん

ホイートストンブリッジ回路の条件は，有名なので知っている人も

多いでしょう．

今回は，ホイートストンブリッジ回路の検流計に電流が流れる場合，抵抗の値によって，どちら方向に電流が流れるのかについての話をします．

ホイートストンブリッジ回路の条件

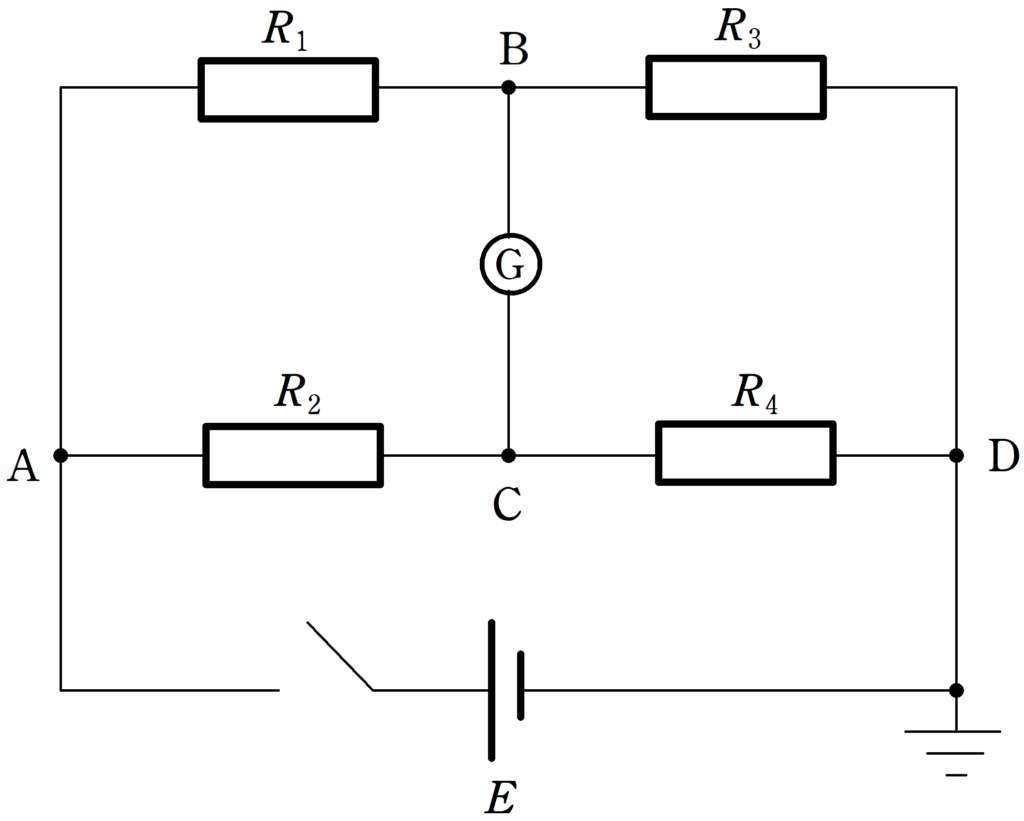
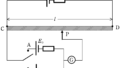
上図に回路において，スイッチを閉じたときに検流計に電流が流れなかった．

このとき，抵抗$R_{1}$，$R_{2}$，$R_{3}$，$R_{4}$の間に次の関係が成り立つ．

$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{3}}{R_{4}}$

($R_{1}R_{4}=R_{2}R_{3}$)

逆に，上の抵抗の関係式が成り立つのであれば，検流計に電流は流れない．

ホイートストンブリッジ回路の検流計に電流が流れる向き
証明

ホイートストンブリッジ回路の検流計に電流が流れる向き

PHYさん

電流の流れる向きは，次のように決まります．

ホイートストンブリッジ回路の検流計に流れる電流の向き

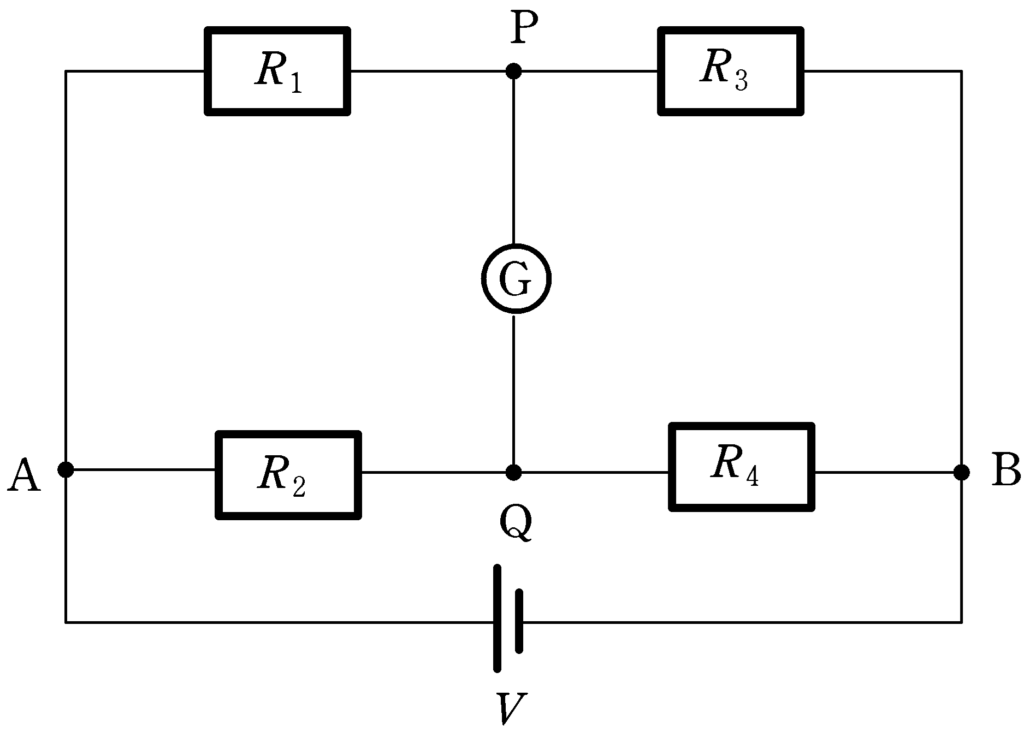
上図の回路において，検流計の内部抵抗や，電池の起電力には無関係に

$R_{1}R_{4}<R_{2}R_{3}$のとき，PからQへ電流が流れる

$R_{1}R_{4}＞R_{2}R_{3}$のとき，QからPへ電流が流れる

PHYさん

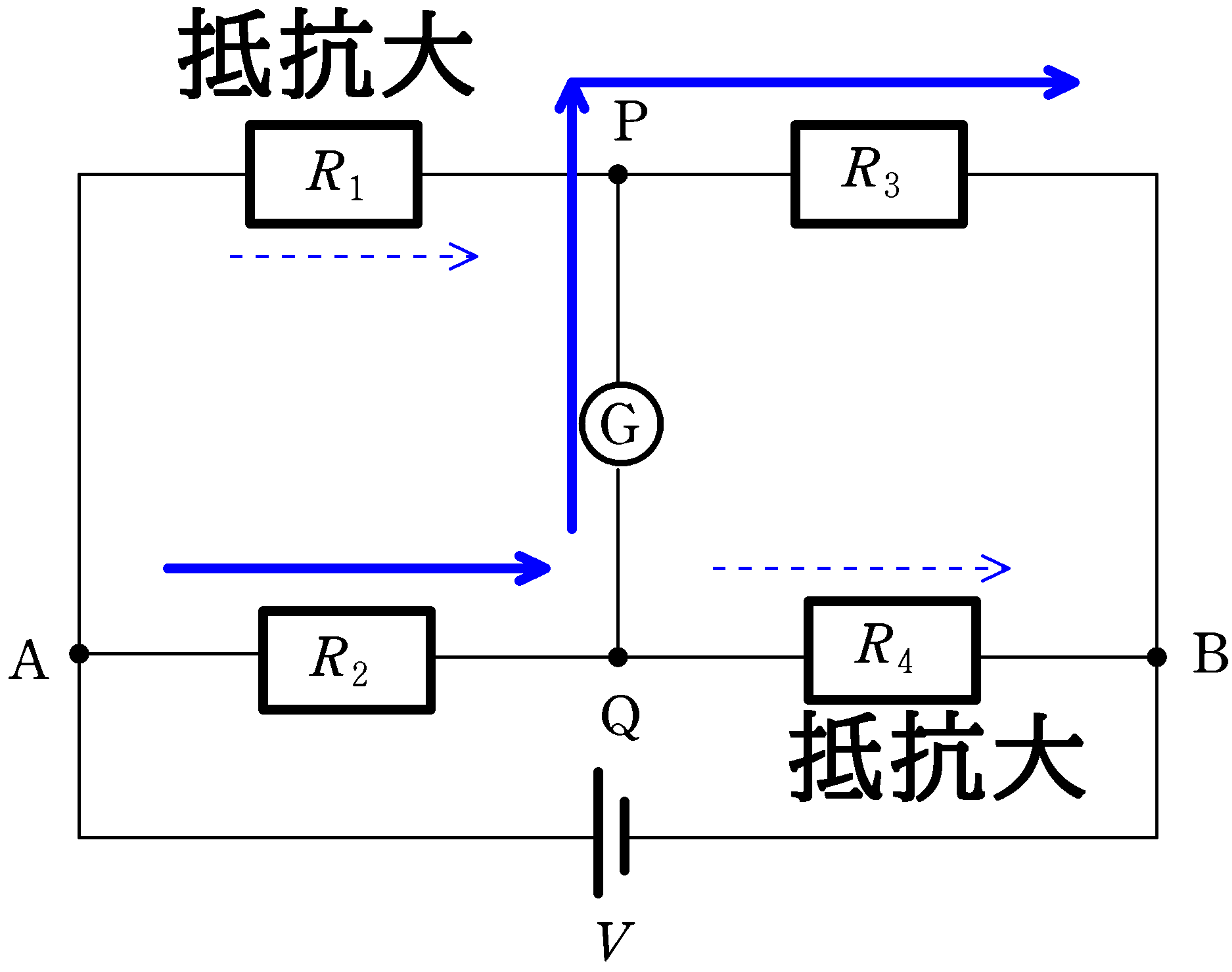
のちに計算をしますが，次のようなイメージをもっておくとよいでしょう．

NEKO

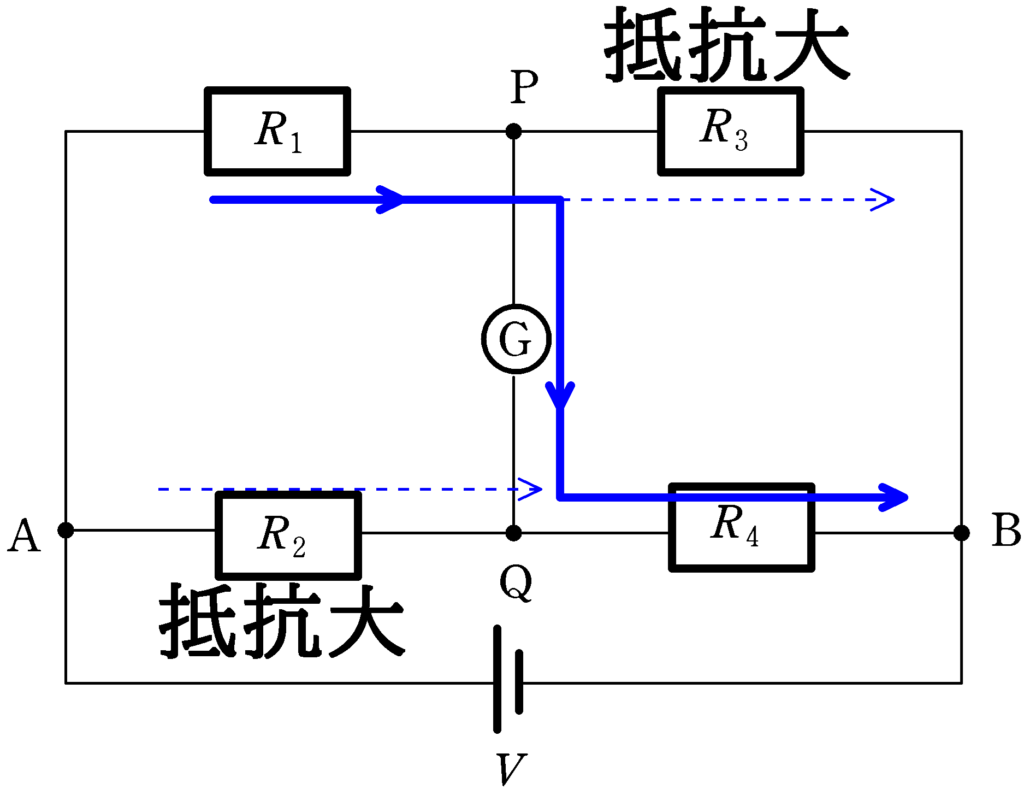
上図では，$R_{2}R_{3}>R_{1}R_{4}$のとき，$R_{2} , R_{3}$それぞれを抵抗が大きいと考えて（実際はそうとは限らないけど）$R_{3}$の抵抗を避けるようにPからQへ流れているんだね．

※　PからQへ流れているだけで$R_{3}$や$R_{2}$の抵抗にも電流は流れます．

PHYさん

はい．では，$R_{1}R_{4}>R_{2}R_{3}$ではどうなるでしょうか．

NEKO

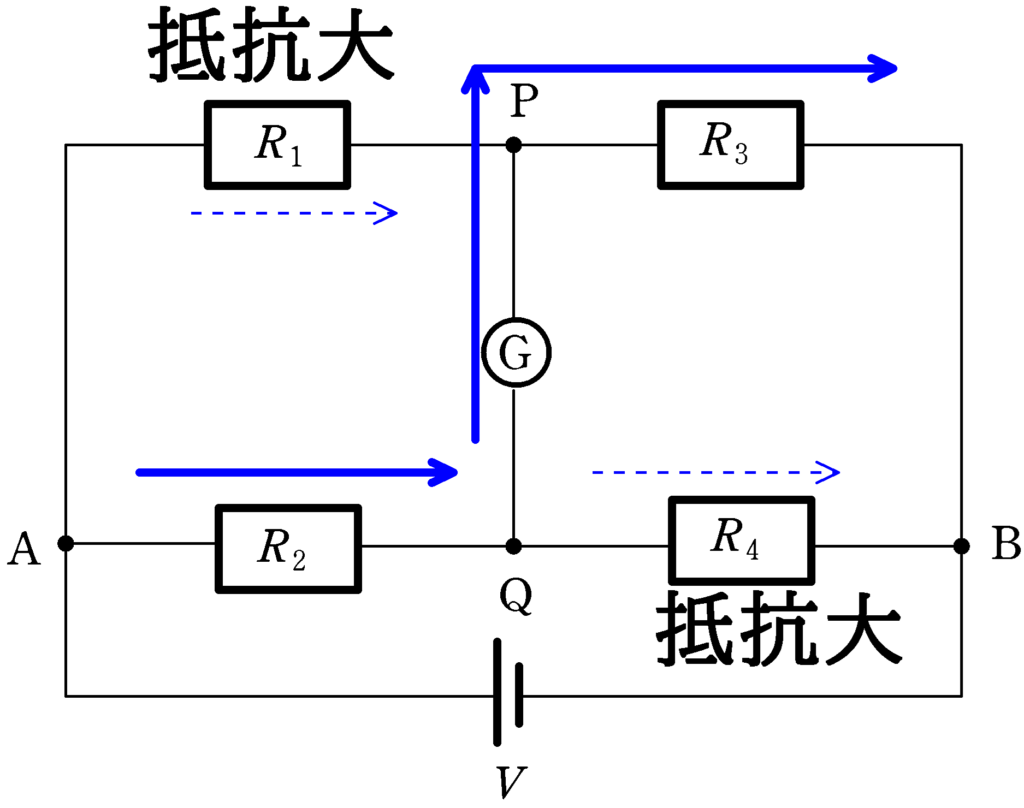
$R_{1}$，$R_{4}$を抵抗が大きいと考えて，$R_{4}$を避けるように，$R_{3}$に流れるのかな．

PHYさん

そういうことです．

では，次に，本当にこの条件でいいのかどうかを計算していきましょう．

証明

PHYさん

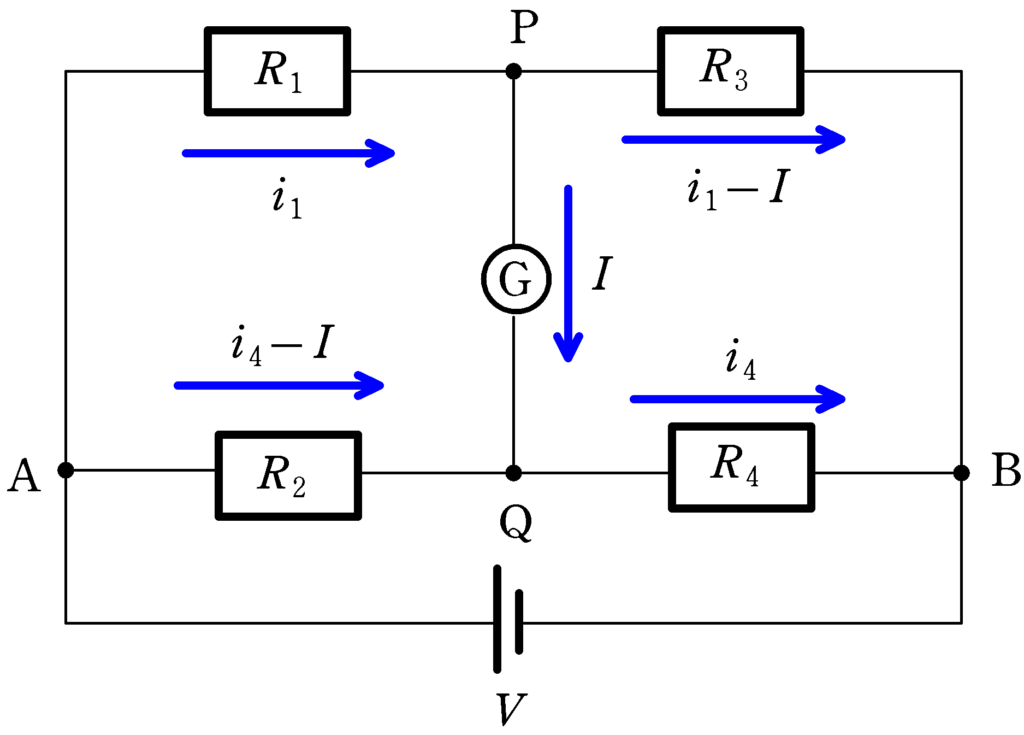
$R_{1}$に流れる電流を$i_{1}$，$R_{4}$に流れる電流を$i_{4}$，検流計に流れる電流を$I$(P→Qを正の向き)とします．電池の起電力は$V$，検流計の内部抵抗を$r$とします．

このように設定すると，キルヒホッフ第1法則より$R_{2}$に流れる電流は$i_{4}-I$，抵抗$R_{3}$に流れる電流は$i_{1}-I$となります．

ここで，

A→P→B
A→Q→B
A→P→Q→A

の3つのキルヒホッフ則を立てます．

※　Bの電位を基準（0）とし，Aの電位を$V$とします．

★　 A→P→B

$V-R_{1}i_{1}-R_{3}(i_{1}-I)=0$

$\eqalign{(R_{1}+R_{3})i_{1}&=R_{3}I+V\cr\\\therefore　i_{1}&=\dfrac{R_{3}I+V}{R_{1}+R_{3}}　\cdots (\ast)}$

★　 A→Q→B

$V-R_{2}(i_{4}-I)-R_{4}i_{4}=0$

$\eqalign{(R_{2}+R_{4})i_{4}&=R_{2}I+V\cr\\\therefore　i_{4}&=\dfrac{R_{2}I+V}{R_{2}+R_{4}}　\cdots (2\ast)}$

★　A→P→Q→A

$V-R_{1}i_{1}-rI+R_{2}(i_{4}-I)=V$

$-R_{1}i_{1}+R_{2}i_{4}=(r+R_{2})I$　$\cdots　(3\ast)$

PHYさん

$(\ast)$，$(2\ast)$を$(3\ast)$に代入して$I$について解きましょう．

$(\ast)$，$(2\ast)$を$(3\ast)$に代入して

$-R_{1}\cdot \dfrac{R_{3}I+V}{R_{1}+R_{3}}+R_{2}\cdot \dfrac{R_{2}I+V}{R_{2}+R_{4}}=(r+R_{2})I$

両辺$(R_{1}+R_{3})(R_{2}+R_{4})$をかけて

$-R_{1}(R_{2}+R_{4})(R_{3}I+V)+R_{2}(R_{1}+R_{3})(R_{2}I+V)=(R_{1}+R_{3})(R_{2}+R_{4})(r+R_{2})I$

PHYさん

展開し，$I$について整理しましょう．

$-R_{1}R_{3}(R_{2}+R_{4})I-R_{1}(R_{2}+R_{4})V+R_{2}^{2}(R_{1}+R_{3})I+R_{2}(R_{1}+R_{3})V=(R_{1}+R_{3})(R_{2}+R_{4})(r+R_{2})I$

$\eqalign{(R_{2}R_{3}-R_{1}R_{4})V&=(R_{1}+R_{3})\left\{(R_{2}+R_{4})(r+R_{2})-R_{2}^{2}\right\}I+R_{1}R_{3}(R_{2}+R_{4})I\\&=(R_{1}+R_{3})(R_{2}r+R_{4}r+R_{2}R_{4})I+R_{1}R_{3}(R_{2}+R_{4})I}$

ここで，$A= (R_{1}+R_{3})(R_{2}r+R_{4}r+R_{2}R_{4}) >0$，$B= R_{1}R_{3}(R_{2}+R_{4}) $とおくと

$(A+B)I=(R_{2}R_{3}-R_{1}R_{4})V$

$\therefore　I=\dfrac{R_{2}R_{3}-R_{1}R_{4}}{A+B}V$

NEKO

だから，$R_{2}R_{3}>R_{1}R_{4}$のとき，$I>0$で，$R_{2}R_{3}<R_{1}R_{4}$のとき，$I<0$となるんだね！