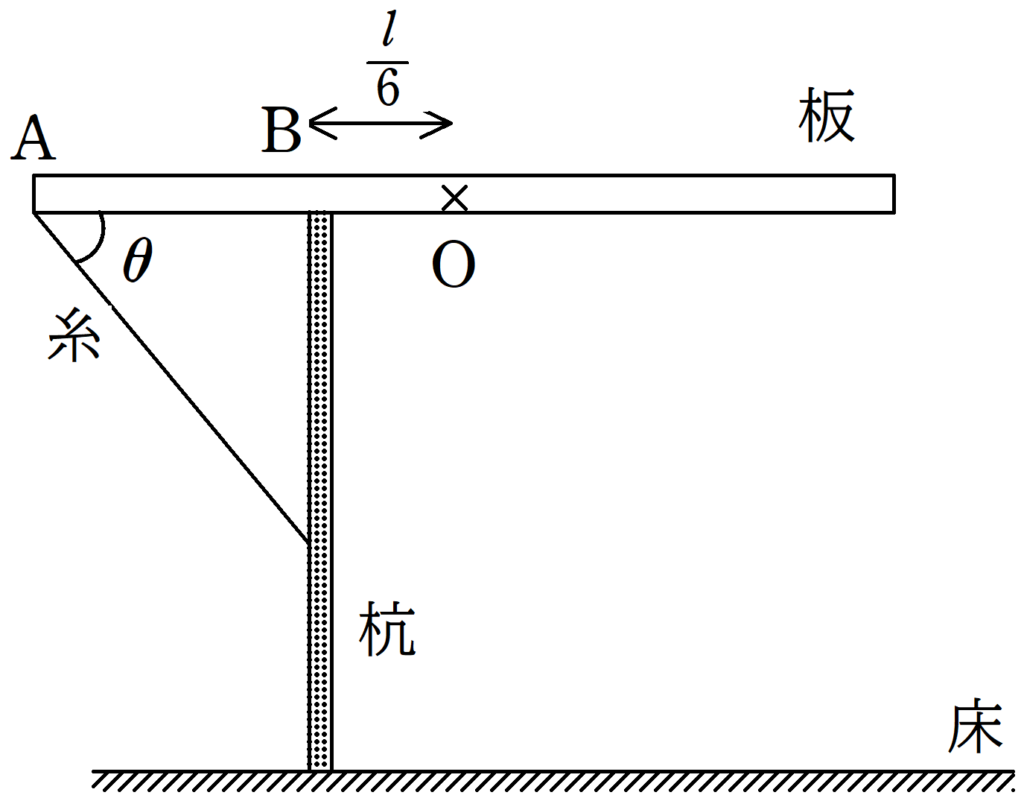
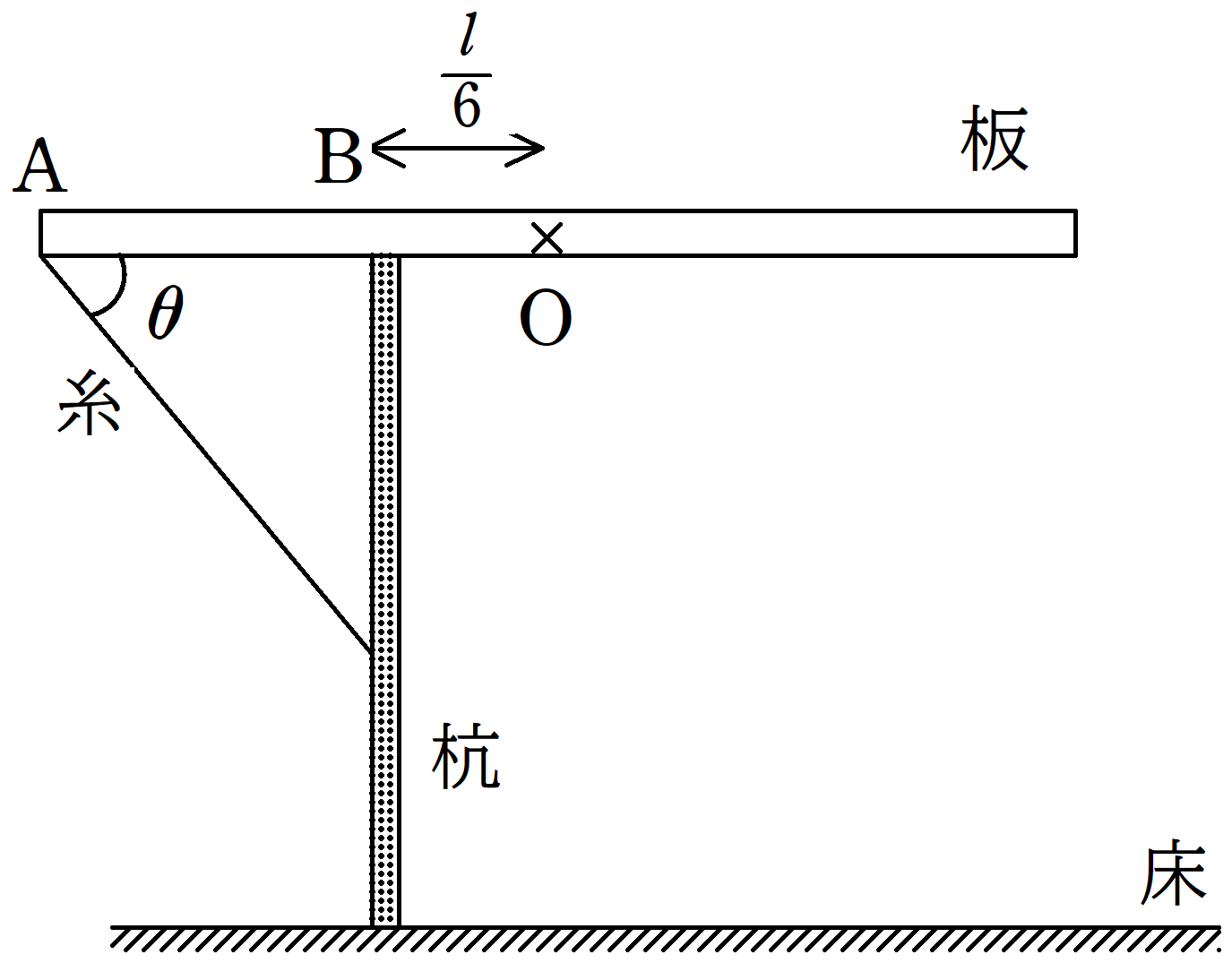
図のように,水平な床に杭が固定されており,杭には板がのせられている.板は一様な密度であり,質量は$m$である.板の長さは$l$であり,その中央に点$\rm O$をとる.点$\rm O$から距離$\dfrac{l}{6}$の場所$\rm B$で杭と接触している.また,板の左端$\rm A$には軽くて伸びない糸が取りつけられており,糸の他端は杭に取りつけられている.板と糸のなす角は$\theta(0<\theta<\dfrac{\pi}{2})$であった.重力加速度の大きさを$g$として,次の問いに答えよ.
(1) $\rm B$にはたらく垂直抗力の大きさを$N$,摩擦力の大きさを$f$,$\rm A$にはたらく張力の大きさを$T$とする.板に関する水平方向と鉛直方向のつり合いの式を立てよ.
(2) 点$\rm B$まわりの力のモーメントのつり合いの式を立てることで張力の大きさ$T$を$m$,$g$,$\theta$を用いて表せ.
(3) (1),(2)より,$N$,$f$を$m$,$g$,$\theta$から必要なものを用いて表せ.
<解答>
(1)
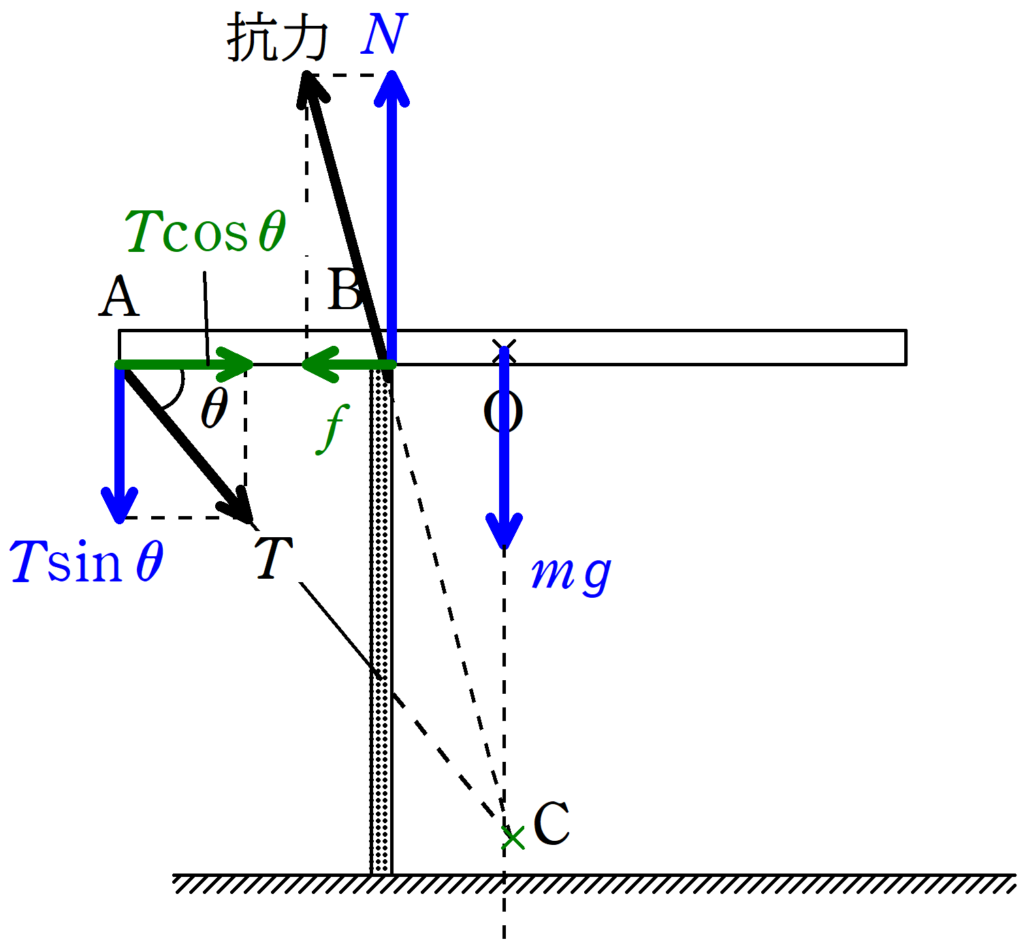

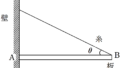
板にはたらく力を図示すると上のようになります.
$\rm O$には重力$mg$が,$\rm A$には張力がはたらきます.
重力と張力の作用線は$\rm C$で交わるので,$\rm C$を通るような向きに$\rm B$に抗力がはたらきます.
$\rm B$にはたらく抗力の水平成分が摩擦力,鉛直成分が垂直抗力です.
張力も水平成分と鉛直成分に分解して,力のつり合いの式を立てましょう.
★ 水平方向のつり合いの式
$f=T\cos\theta$ $\dots (\ast)$ (答)
★ 鉛直方向のつり合いの式
$N=T\sin\theta +mg$ $\dots (2\ast)$ (答)
(2)
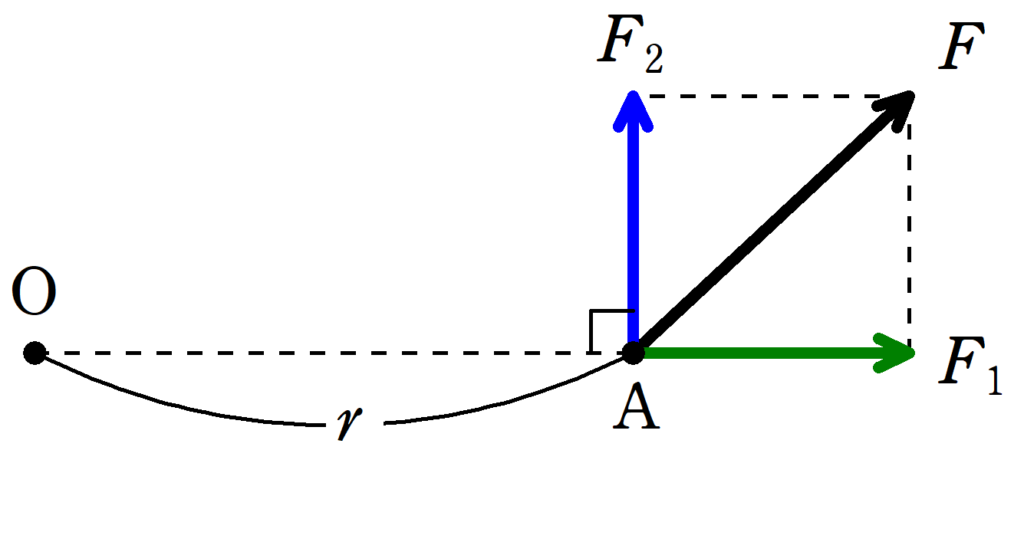
中心$\rm O$から距離$r$の点$\rm A$を始点とした大きさ$F$の力がはたらいている.この力の$\rm OA$方向の成分を$F_{1}$,$\rm OA$に垂直な成分を$F_{2}$とすると,力$F$の点$\rm O$まわりの力のモーメントの大きさ$N$は
$N=rF_{2}$
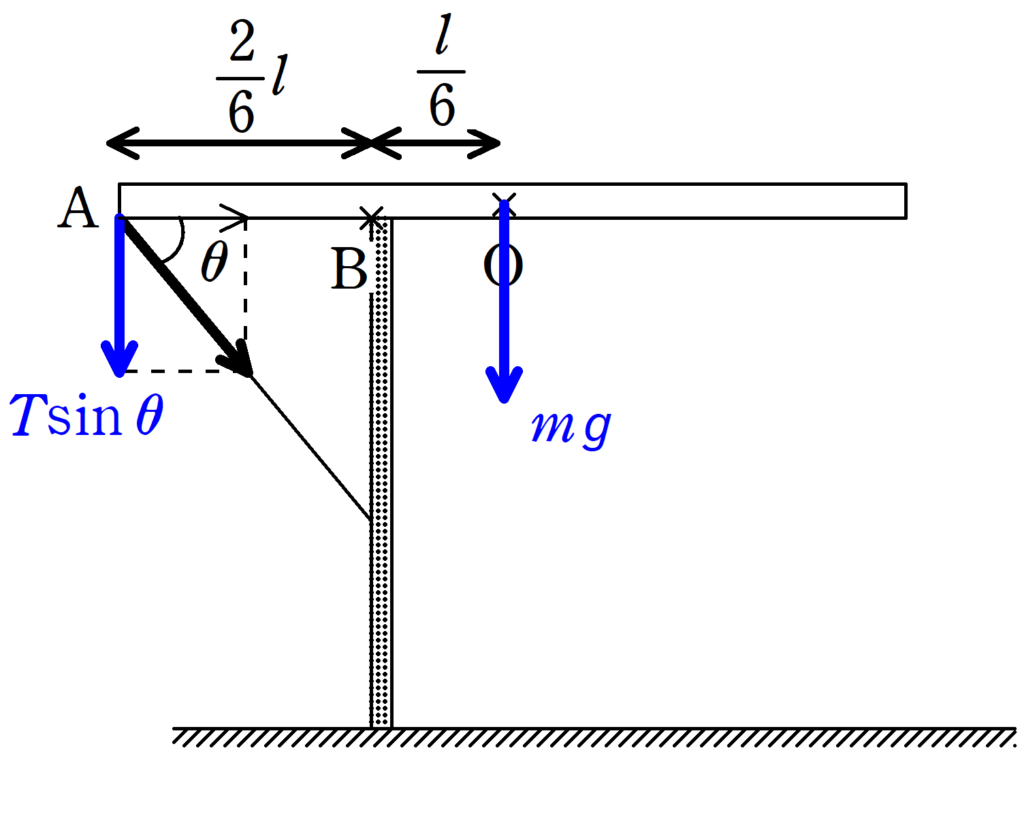

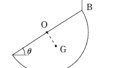
$\rm B$まわりの力のモーメントのつり合いの式を立てます.
力のモーメントをもっているのは,上の青い矢印である,$T\sin\theta$と$mg$のみです.$\rm B$にはたらく力は距離$0$なので,力のモーメントは$0$です.
★ $\rm B$まわりの板に関する力のモーメントのつり合いの式
$\dfrac{2}{6}l\cdot T\sin\theta=\dfrac{l}{6}\cdot mg$
$\therefore T=\dfrac{mg}{2\sin\theta}$ (答)
(3)
(2)の答えを$(\ast)$,$(2\ast)$に代入して
$(\ast)$より
$\eqalign{f&=T\cos\theta\\&=\dfrac{mg}{2\tan\theta}}$ (答)
$(2\ast)$より
$\eqalign{N&=T\sin\theta +mg\\&=\dfrac{3}{2}mg}$ (答)

コメント