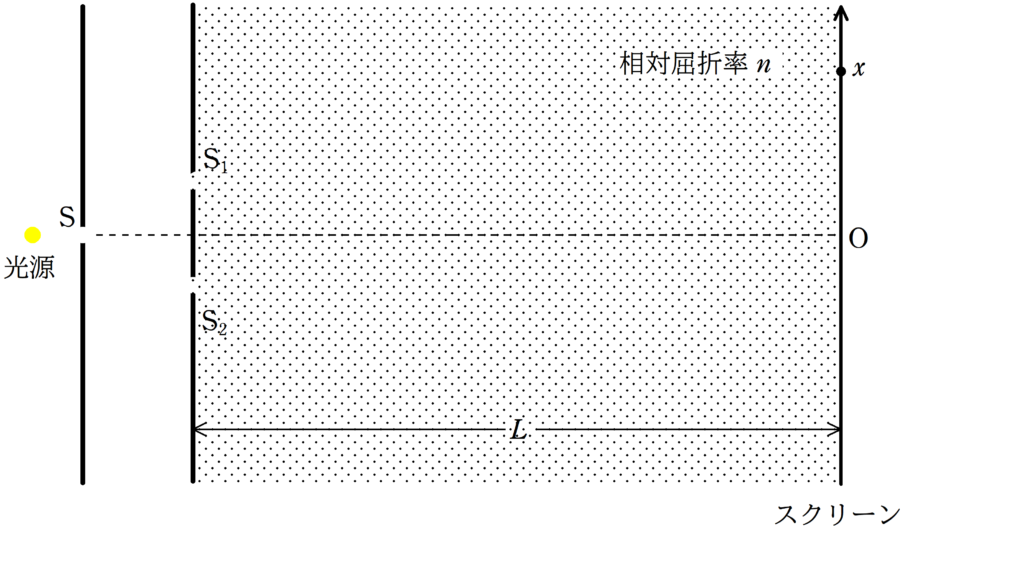
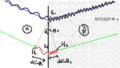
上図のように単スリット$\rm S$,2スリット$\rm S_{1} , S_{2}$のついたて,スクリーンが平行に設置されている.
スリット$\rm S_{1} , S_{2}$の距離が$d$,スリット$\rm S_{1} , S_{2}$のついたてとスクリーンまでの距離が$L$である.
スリット$\rm S$に空気中での波長$\lambda$の単色光を当てたところ,単色光は$\rm S_{1} , S_{2}$を通り,スクリーンに明暗の縞模様ができた.
(1) 明線との明線の間隔を求めよ.
次に,ついたてとスクリーンの間を空気に対する相対屈折率$n$の透明物質で満たした.
(2) 透明物質を入れた後の明線と明線の間隔を求めよ.
<解答>
(1)

(1)は前回と同じだよ.
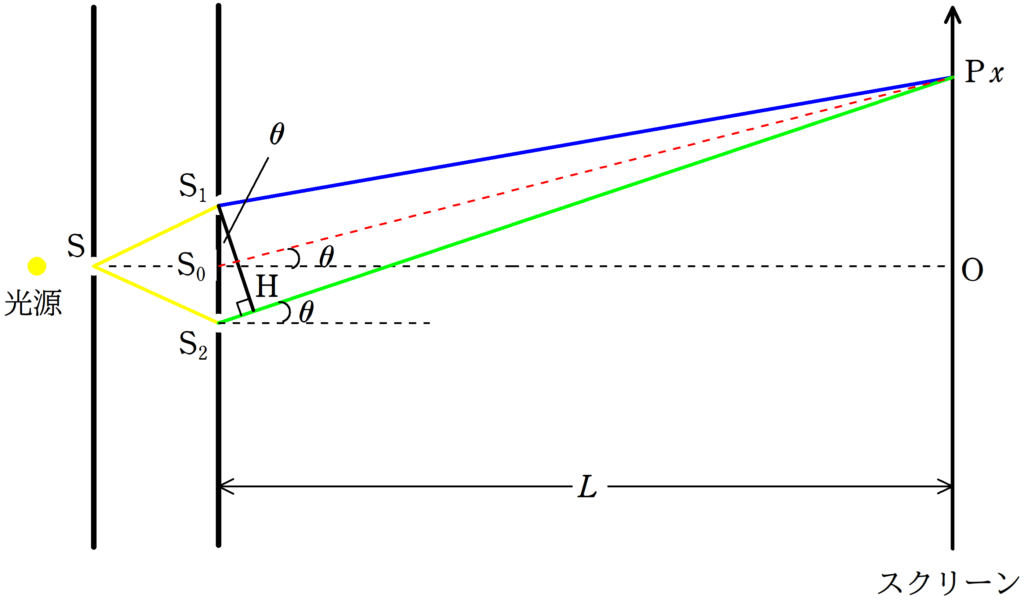

なので,簡単に答えをかくね.
まず,$\rm S_{1}$と$\rm S_{2}$の中点からスクリーンに下した垂線の足を原点$\rm O$として,スクリーン上の上方向を$x$軸の正方向にとります.
そして,座標$x$における明線条件を考えていきましょう.
$\eqalign{\dfrac{\rm S_{2}P-S_{1}P}{\lambda}&=m\cr d\dfrac{x_{m}}{L}&=m\lambda\cr x_{m}&=\dfrac{mL\lambda}{d}}$
したがって
$\Delta x=\dfrac{L\lambda}{d}$

ちなみに,$d=1.0 \rm mm$,$L=1.0 \rm m$,$\lambda=5.0×10^{-7} \rm m$の場合は,明線の間隔は$\Delta x=0.50 \rm mm$となります.
(2)

透明物質を全体で満たすなら,経路差は変わらないんじゃないの?

前と同じですが,干渉条件は,経路差が本質ではなく,位相差が大事なのです.
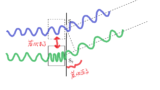
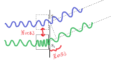
屈折率$n$の透明物質に入ると,空気中のときの$\dfrac{1}{n}$倍の波長になります.
そうなることで,経路差に内の波の数に差が出てきます.
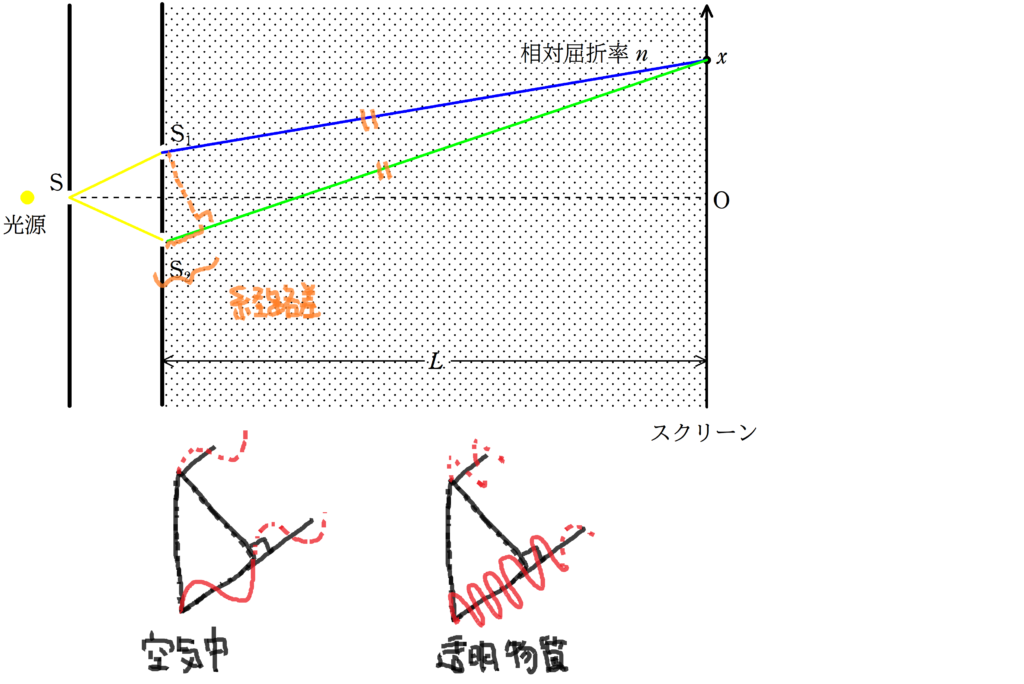

つまり,明線条件は次のようになるんだね.
$\dfrac{d\dfrac{x_{m}}{L}}{\dfrac{\lambda}{n}}=m$
$\therefore \Delta x=\dfrac{L\lambda}{nd}$

ということで,答えは$\dfrac{L\lambda}{nd}$だね.

コメント
[…] ヤングの実験演習問題②問題上図のように単スリット$rm S$,2スリット$rm … […]