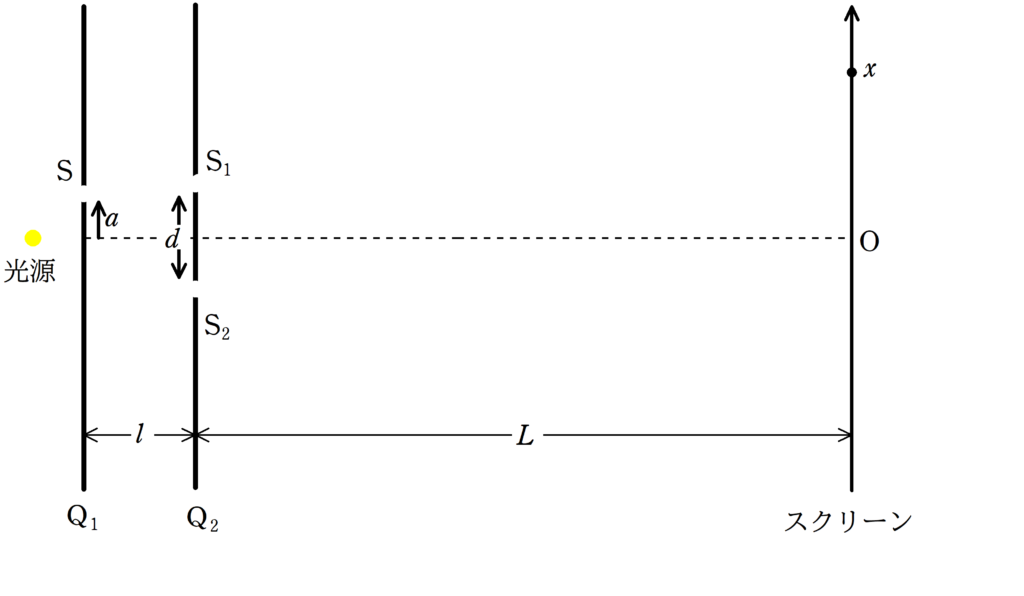
ついたて$\rm Q_{1}$,$\rm Q_{2}$,スクリーンが平行に設置されている.
$\rm Q_{1}$と$\rm Q_{2}$の距離は$l$,$\rm Q_{2}$とスクリーンの距離は$L$である.
$\rm Q_{2}$には間隔$d$のスリットがあり,スリットの垂直二等分線と$\rm Q_{1}$との交点にスリット$\rm S$がある.
スリット$\rm S$の左側より,単色光で波長$\lambda$の光を当てたところ,スクリーンに明暗の縞模様ができた.
このとき,次の問いに答えよ.
ただし,$d$は$L$に比べて十分小さいとする.
(1) スリット$\rm S$を図の上方向に$a$だけ移動させたところ,スクリーンにうつる明暗が移動した.どの向きにどれだけ移動したか答えよ.ただし,$a$や$d$は$l$に比べて十分小さいとしてよい.
(2) (1)に続いて,$\rm Q_{2}$とスクリーンの間を空気に対する相対屈折率$n$の透明物質で満たした.このとき,明線の間隔はどれほどか.
<解答>

ヤングの実験演習問題シリーズの第3回です.
前回の内容はこちら.
(1)

今回は,スリット$\rm S$が動いたので,左側の経路にも位相差が生じます.
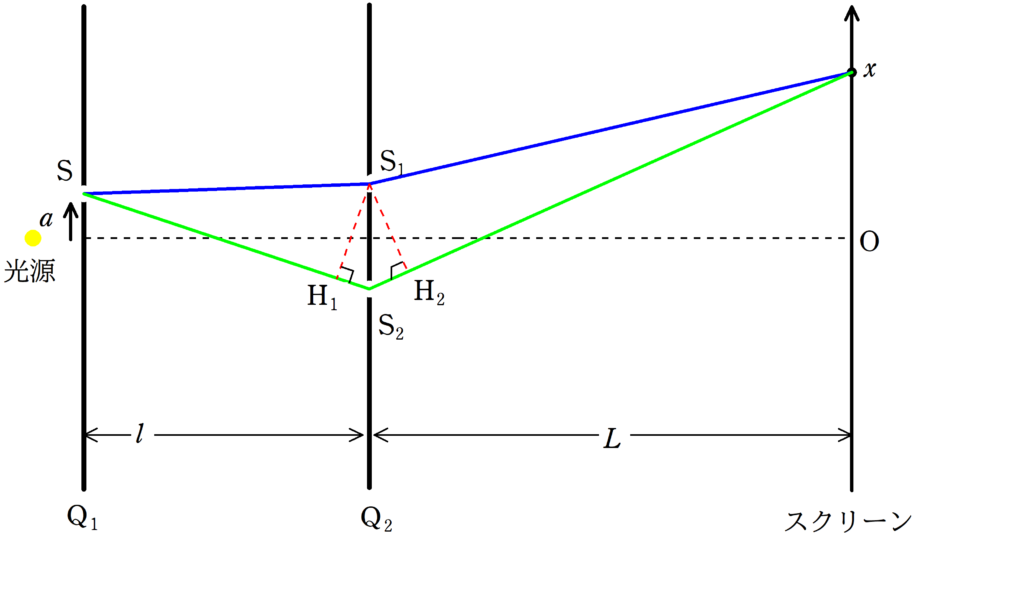

あらかじめ座標を設定しておきましょう.
$\rm S_{1}$と$\rm S_{2}$の垂直二等分線とスクリーンの交点を原点として,スクリーン上のに$x$座標をとります.
スクリーンの上方向を$x$の正の方向としましょう.
一般的な座標$x$(点$\rm P$)に明線があるときを考えます.
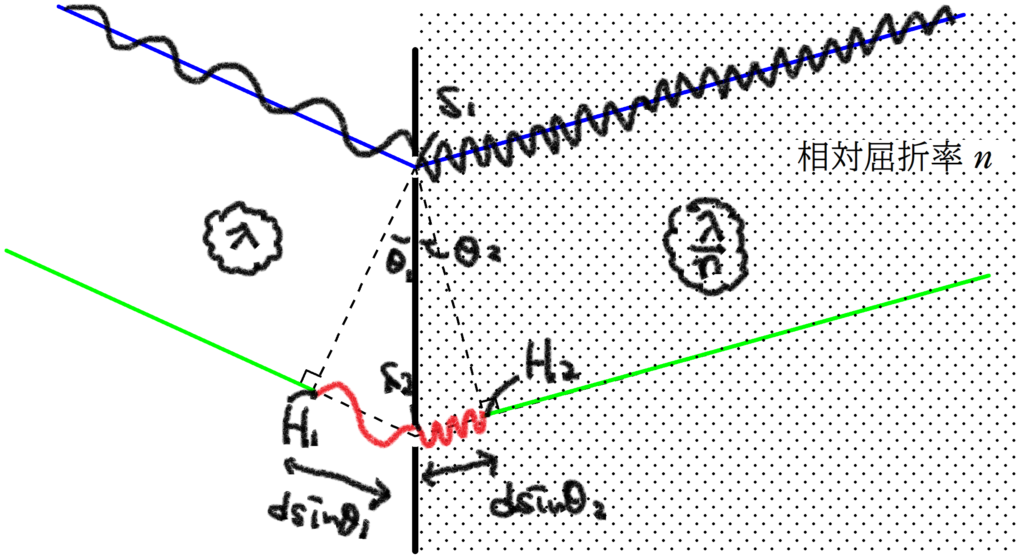
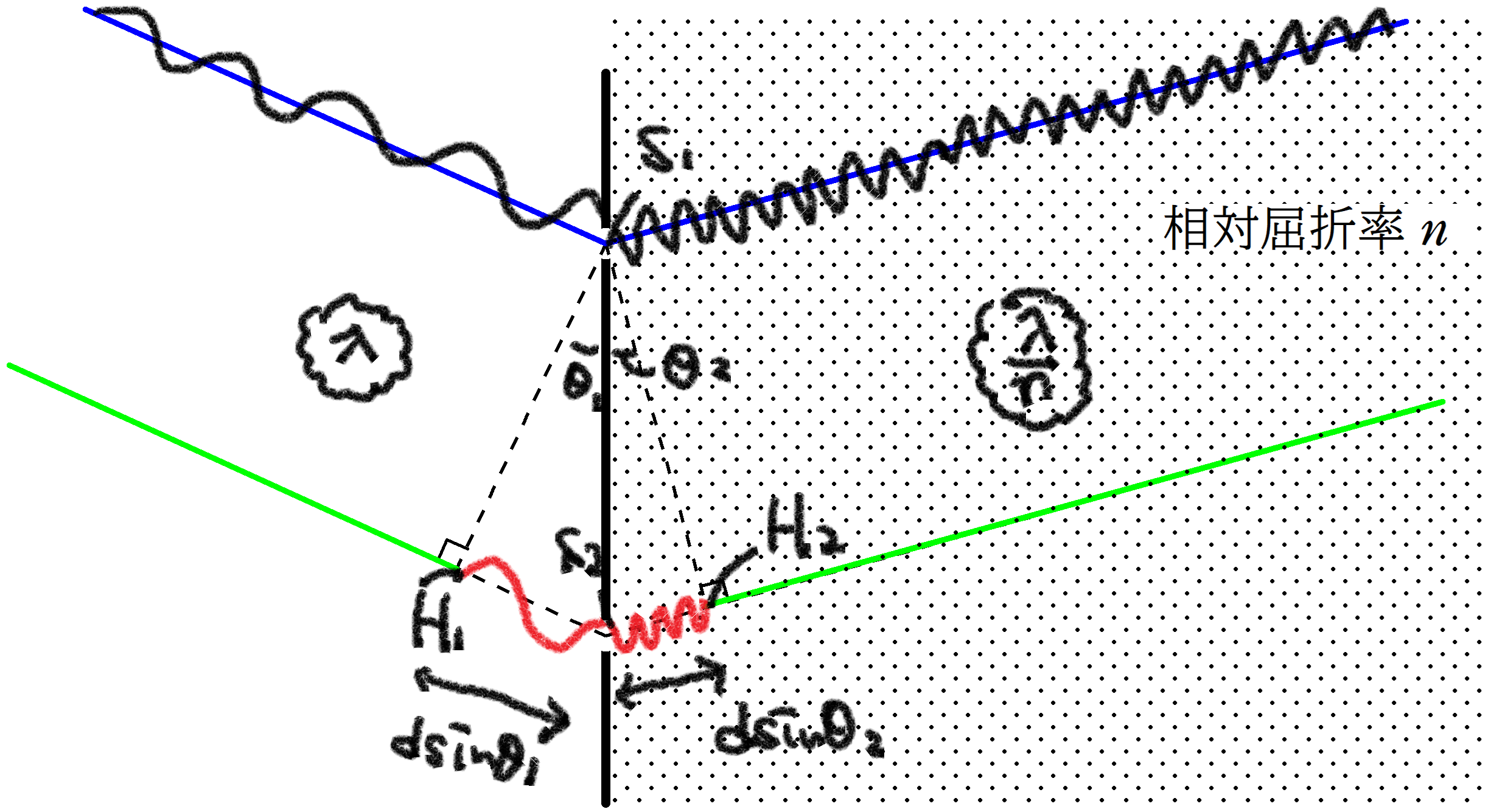
さて,上図のように,$\rm Q_{1}Q_{2}$の間と$\rm Q_{2}$とスクリーンの間のどちらでも緑の方の経路が長くなっていますね.
$\rm S_{1}$から$\rm SS_{2}$,$\rm S_{2}P$に下した垂線の足をそれぞれ,$\rm H_{1}$,$\rm H_{2}$とします.

すると,$\rm H_{1}S_{2}+S_{2}H_{2}$の長さの分,緑色の経路が長くなるんだね.
そして,この経路の中にある波の数が整数個だったら,スクリーンで明線ができるんだね.
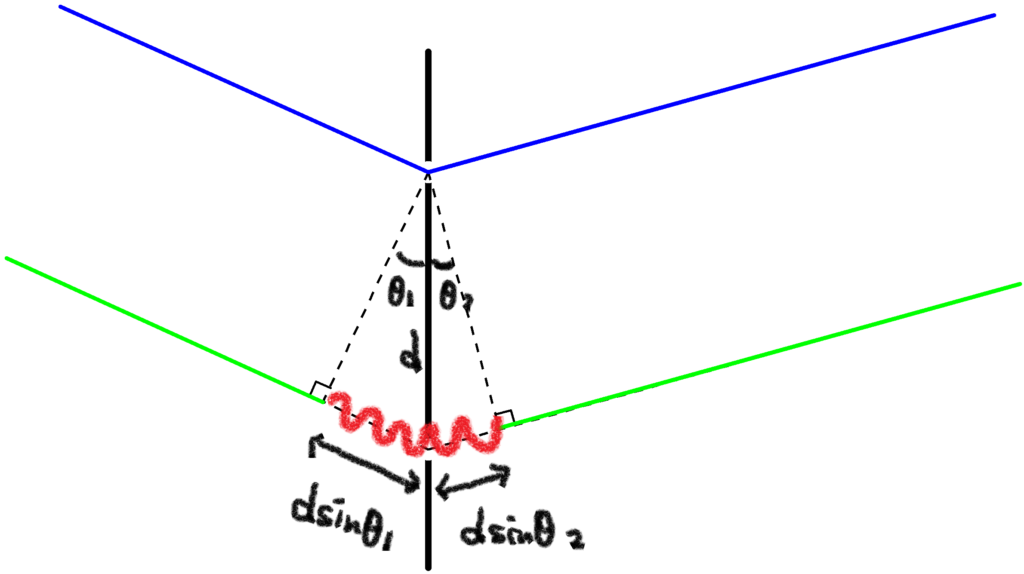

上図のように角度を設定すると,経路差は
$d\sin\theta_{1} +d\sin\theta_{2}$
となります.
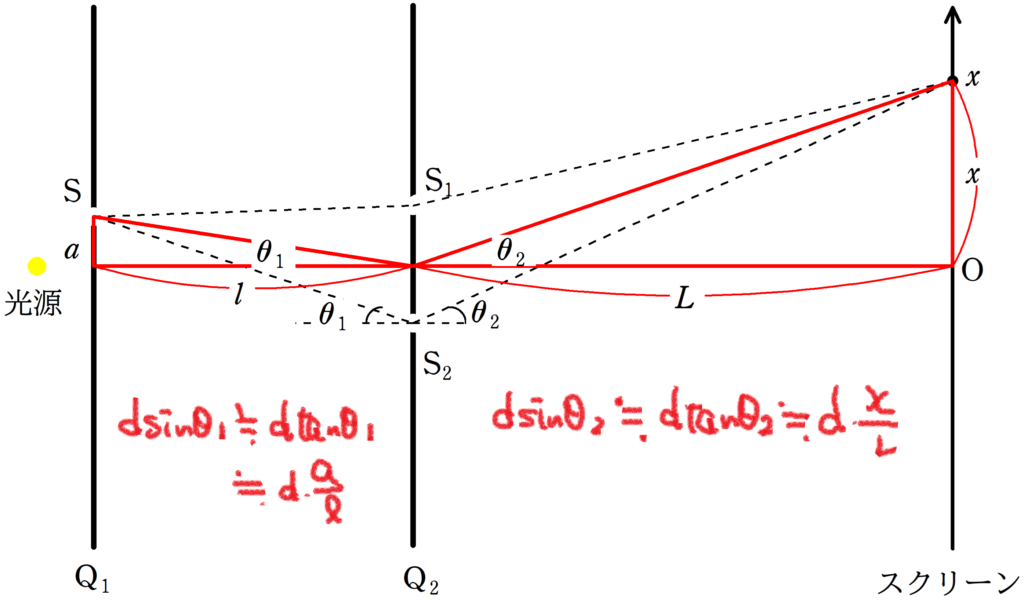

今までと同様に,近似式が使えるね.
$d\sin\theta_{1}\approx d\tan\theta_{1}\approx d\dfrac{a}{l}$
$d\sin\theta_{2}\approx d\tan\theta_{2}\approx d\dfrac{x}{L}$

はい.
以上から,整数$m$を使って,明線の条件は次のようになります.
ちなみに,波の数は次ように表すことができます.
波の波長を$\lambda$(波1個分の長さ),波の個数を$N$,波全体の長さを$\Delta L$とすると,次の関係式が成り立つ.
$\Delta L=N\cdot \lambda$
$\therefore N=\dfrac{\Delta L}{\lambda}$
★ 明線条件
$\dfrac{d\dfrac{a}{l}}{\lambda}+\dfrac{d\dfrac{x}{L}}{\lambda}=m$

この式を$x$について解きます.
$\eqalign{d\dfrac{a}{l}+d\dfrac{x}{L}&=m\lambda\cr x&=\dfrac{mL\lambda}{d}-\dfrac{La}{l}}$

もともとは,$x=\dfrac{mL\lambda}{d}$だったので,$-\dfrac{La}{l}$ずれていることがわかるね.
ただ,もっと簡単に,$m=0$を代入して
$x_{0}=-\dfrac{La}{l}$
となることを確認するだけでもいいよ.もともと$m=0$の明線は$x=0$にあったんだから,やっぱり$-\dfrac{La}{l}$ずれたことが確認できるね.
答え $x$軸の負の向き(図の下向き)に$\dfrac{La}{l}$移動した.
(2)

次の問題は$\rm Q_{2}$とスクリーンの間を空気に対する相対屈折率$n$の媒質で満たすことで,波長が$\dfrac{\lambda}{n}$となります.

経路差は変わらないけど,波の数の差が変化するんだね.
次数$m$の明線ができる座標を$x_{m}$とすると,明線条件は次のようになるよ.
★ 明線条件
$\dfrac{d\dfrac{a}{l}}{\lambda}+\dfrac{d\dfrac{x_{m}}{L}}{\dfrac{\lambda}{n}}=m$
$\therefore$ $x_{m}=\dfrac{mL\lambda}{nd}-\dfrac{La}{nl}$

明線間の距離$\Delta x$を求めるには,$x_{m+1}$と$x_{m}$の差をとればいいね.
$x_{m+1}=\dfrac{(m+1)L\lambda}{nd}-\dfrac{La}{nl}$
より
$\eqalign{\Delta x&=x_{m+1}-x_{m}\\&=\left\{\dfrac{(m+1)L\lambda}{nd}-\dfrac{La}{nl}\right\}-\left\{\dfrac{mL\lambda}{nd}-\dfrac{La}{nl}\right\}\\&=\dfrac{L\lambda}{nd}}$
したがって,答えは$\Delta x=\dfrac{L\lambda}{nd}$



コメント
[…] ヤングの実験演習問題③問題ついたて$rm Q_{1}$,$rm Q_{2}$,スクリーンが平… PHYさん […]