twitterの問題22の解答

<解答>

等加速度運動の対称性を利用すれば一発です．(下記事参照)

投げ上げ運動の際の対称性の理由を$v-t$グラフで考える．

NEKO 投げ上げ運動の際には，次のことをよく使うね． 投げ上げ運動と対称性 時刻$t=0$において，速さ$v_{0}$で投げ上げたときの運動を考える． 投げ上げた地点を原点として上向きに$y$座標をとる． 最高点に達する時刻を$T$とする...

physicmath.net

2021.02.23

物体には重力のみはたらく．重力を$y$方向と$x$方向に分解すると，$y$軸負の方向に一定の加速度をもつことがわかる．その加速度の大きさを$g_{y}$とすると，$y$軸方向の初速が$v_{y}$なので，時刻$t$における$y$方向の速度$v$は等加速度運動の速度の式より

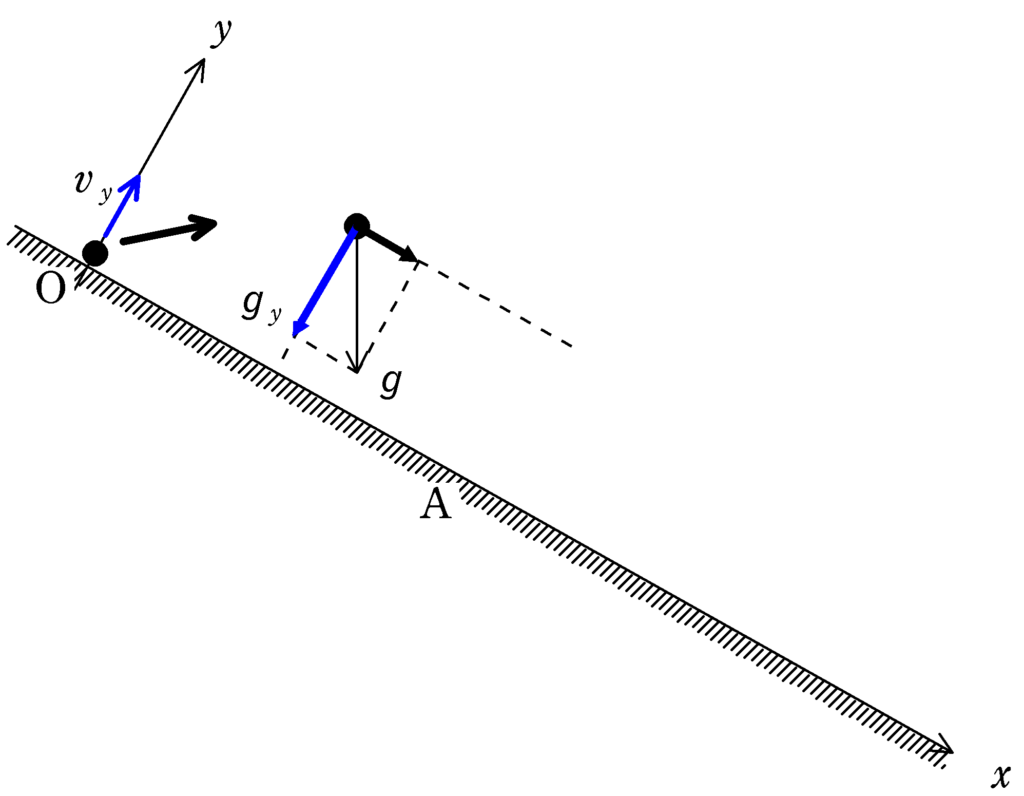
$v=v_{y}-g_{y}t$

となる．これを$v-t$グラフにかくと，$v$$=v_{y}-g_{y}$$t$なので，傾きが$-g_{y}$の直線の式になる．※$y$$=b-a$$x$の形と同じ．

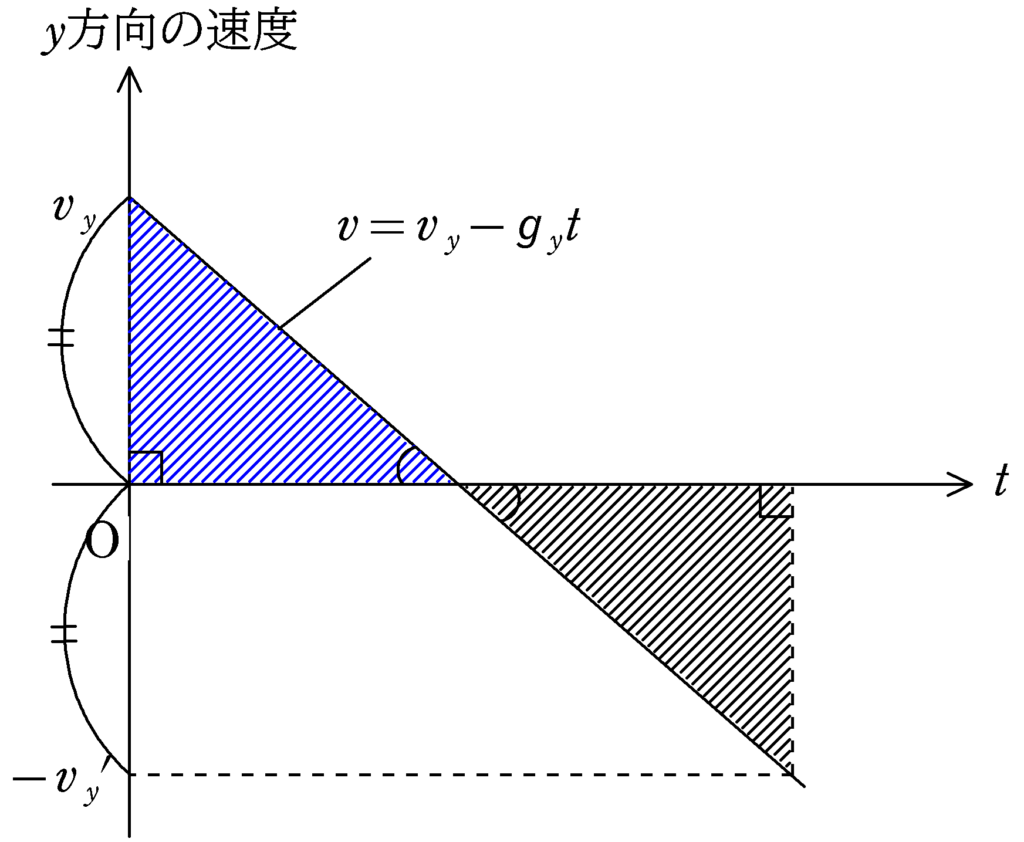
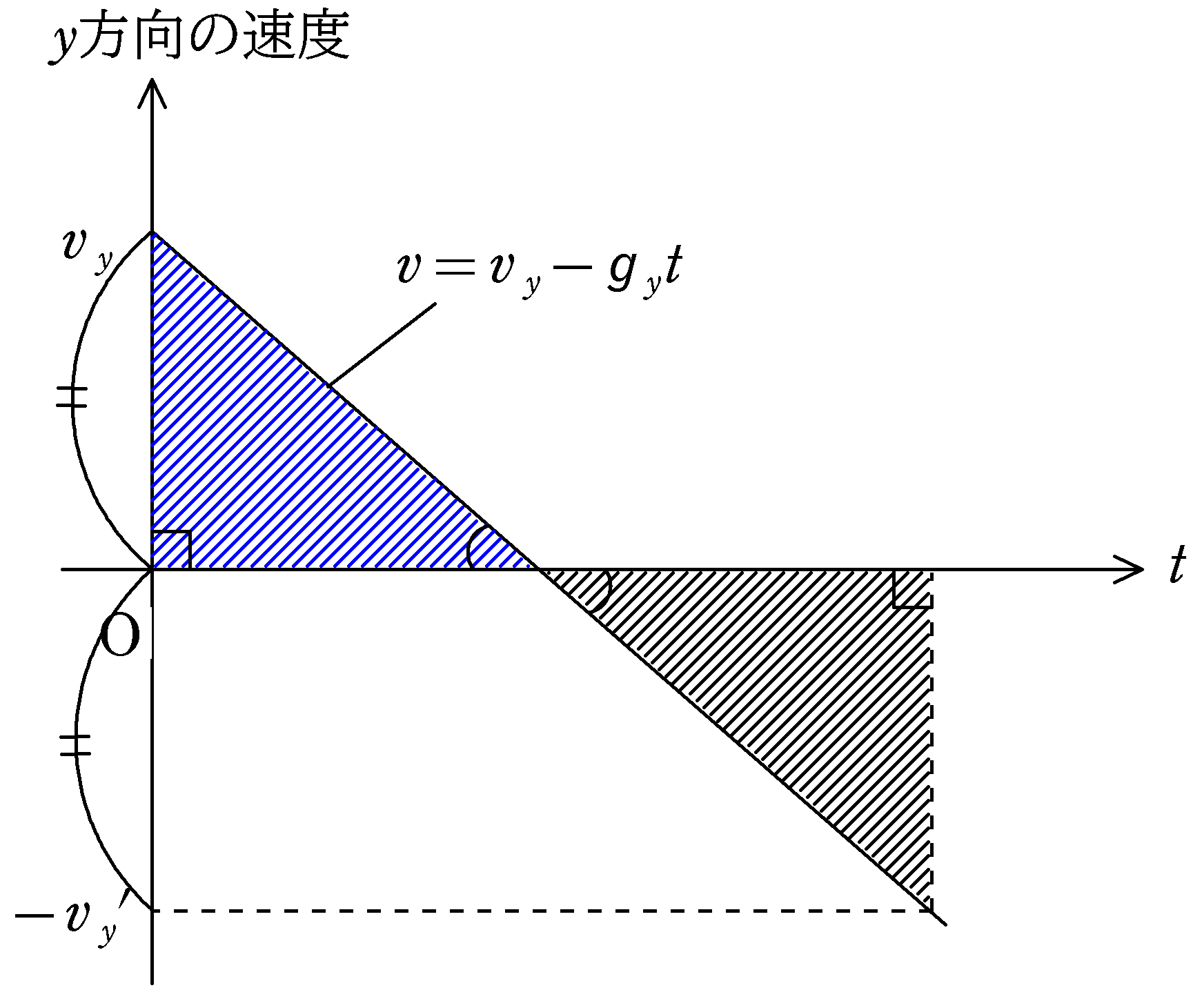
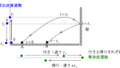
また，$v-t$グラフの面積は$y$方向の移動距離である．上図の青色の直角三角形の面積は初速を与えてから$y$方向の最高点にいくまでに$y$方向に移動した距離であり，黒い方向の直角三角形は最高点から再び斜面にもどってくるまでに$y$方向に移動した距離である．この距離は等しいので，上図の青い直角三角形と黒の直角三角形の面積は同じである．

また，対頂角が等しいことから青い直角三角形と黒の直角三角形は相似であり，面積が等しいことから合同であることがわかる．すると，2つの直角三角形の高さ部分は等しくなるはずなので，

$v_{y}=v_{y}’$

となる．(2)が正解(答)

※つまり投げ出す角度には依らない．