投げ上げ運動の際の対称性の理由を$v-t$グラフで考える．

分野別

2021.02.23

NEKO

投げ上げ運動の際には，次のことをよく使うね．

投げ上げ運動と対称性

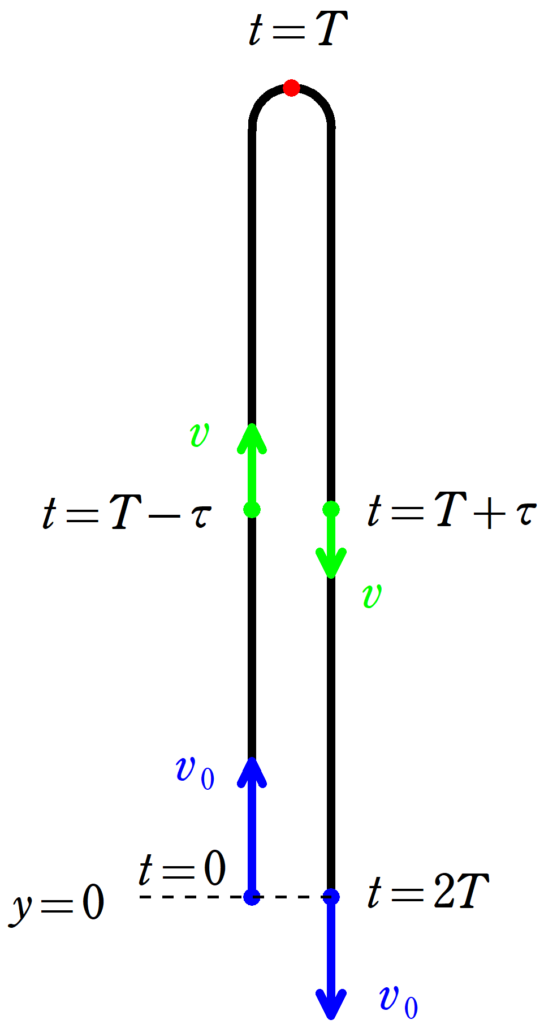
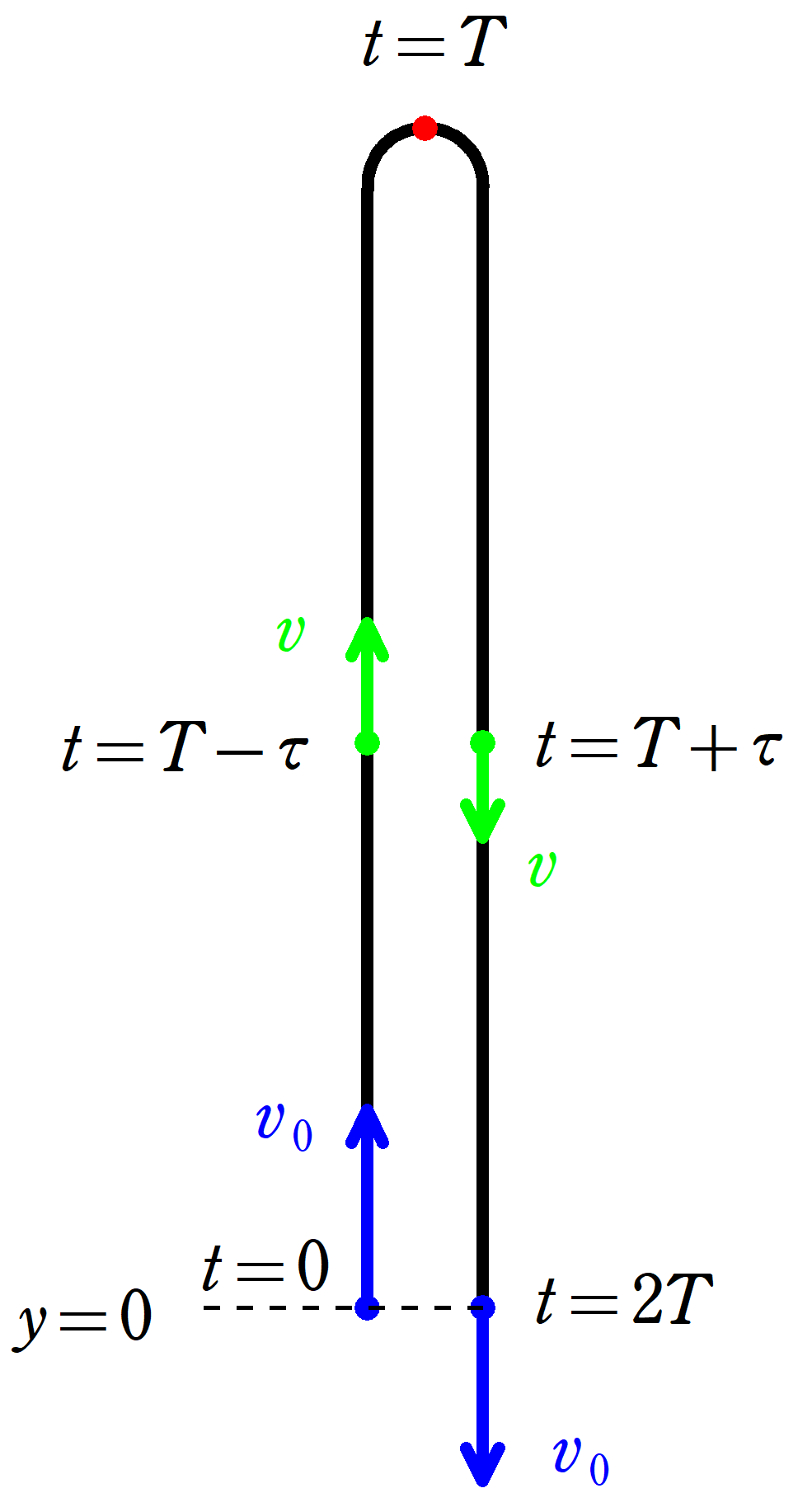
時刻$t=0$において，速さ$v_{0}$で投げ上げたときの運動を考える．

投げ上げた地点を原点として上向きに$y$座標をとる．

最高点に達する時刻を$T$とする．

時刻$t$における速度$v(t)$と座標$y(t)$について，次の関係が成り立つ．

運動$0\leqq \tau \leqq T$について

$|v(T-\tau)|=|v(T+\tau)|$

$y(T-\tau)=y(T+\tau)$

NEKO

たとえば，最高点に達する3秒前と3秒後の速さと高さは同じだってことだね．

なぜ，このようなことになるのかを$v-t$グラフを利用して確認しましょう．

★　等加速度運動の式

鉛直上向きに座標をとると，加速度は重力加速度の大きさを$g$とすれば，$-g$．

さらに，初速度を$v_{0}$とする．

すると，時刻$t$における速度$v$は

$v=v_{0}-gt$

NEKO

$v$$=v_{0}-g$$t$

について，縦軸を$v$，横軸を$t$とした$v-t$グラフをかきましょう．

すると，$v_{0}$は縦軸の切片の値になり，$-g$は直線の傾きになるね．

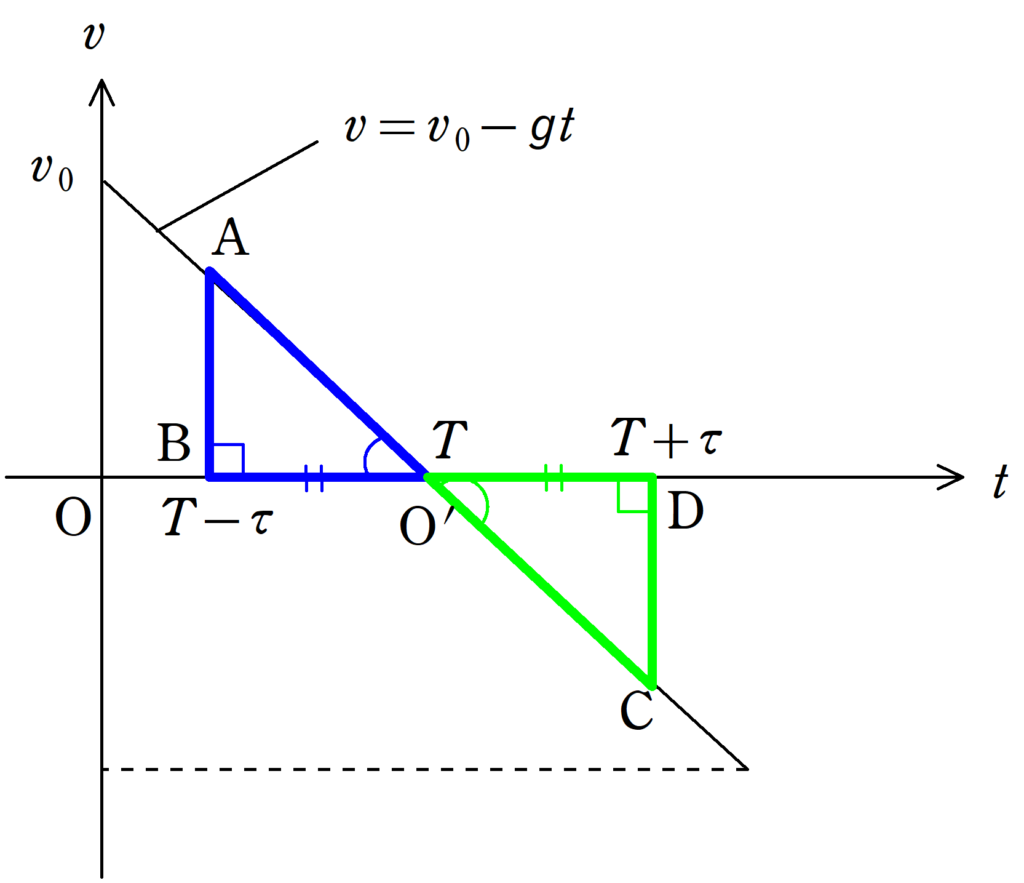
この直線と$t$軸との共有点の$t$座標を$T$として，下図のように$\triangle\rm O^{\prime}AB$と$\triangle\rm O^{\prime}CD$について考えます．

このとき，

${\rm O^{\prime}B}={\rm O^{\prime}D}=\tau$

です．

$t=T$は速度が$0$の時刻なので，最高点に達する時刻となります．

時刻$t=T$より時間$\tau$だけ前の速さは$\rm AB$の長さに対応し，時刻$t=T$より時間$\tau$だけ後の速さは$\rm CD$の長さに対応しています．

${\rm AB}={\rm CD}$

を示すために，$\triangle\rm O^{\prime}AB$と$\triangle\rm O^{\prime}CD$が合同であることを示しましょう．

${\rm O^{\prime}B}={\rm O^{\prime}D}$　(仮定)　$\dots　(\ast)$

${\angle \rm O^{\prime}BA}={\angle \rm O^{\prime}DC}=90°$　(仮定)　$\dots　(2\ast)$

${\rm BO^{\prime}A}={\rm DO^{\prime}C}$　(対頂角)　$\dots　(3\ast)$

$(\ast)$~$(3\ast)$より，1辺とその両端の角がそれぞれ等しいので，

$\triangle\rm O^{\prime}AB \equiv \triangle\rm O^{\prime}CD$

NEKO

したがって，対応する辺を考えれば，

${\rm AB}={\rm CD}$

となるんだね．

つまり，最高点に達する時刻$T$より，$\tau$前の速さと$\tau$後の速さが同じであることが示されたね．

さらに，$\triangle\rm O^{\prime}AB$と$\triangle\rm O^{\prime}CD$の面積は移動距離を表すので，最高点に達する時刻$T$より$\tau$前の高さと$\tau$後の高さが同じであることがわかるね．