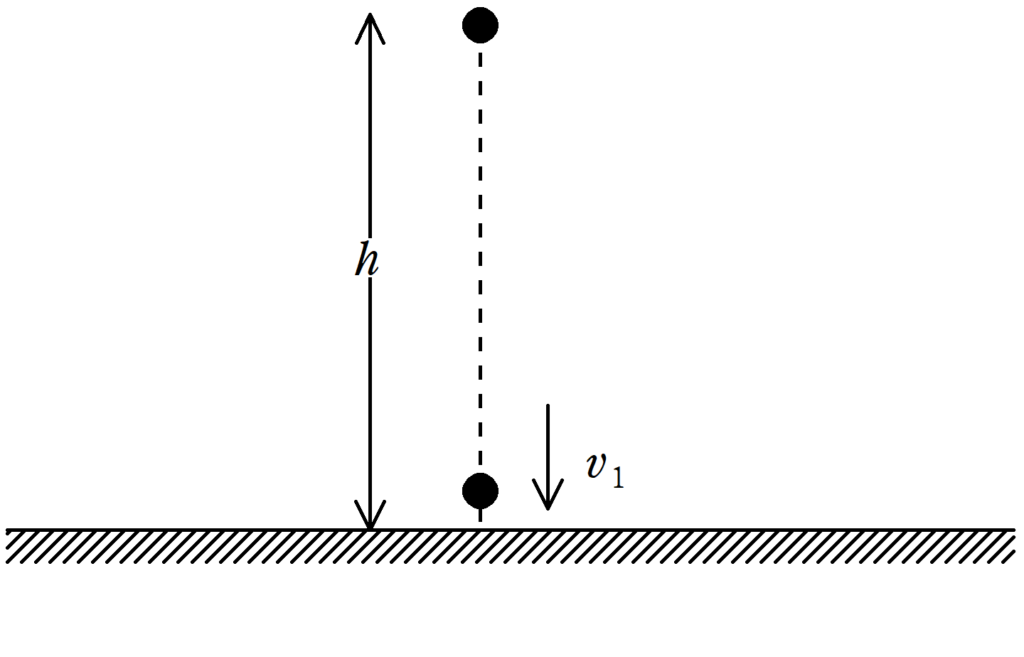
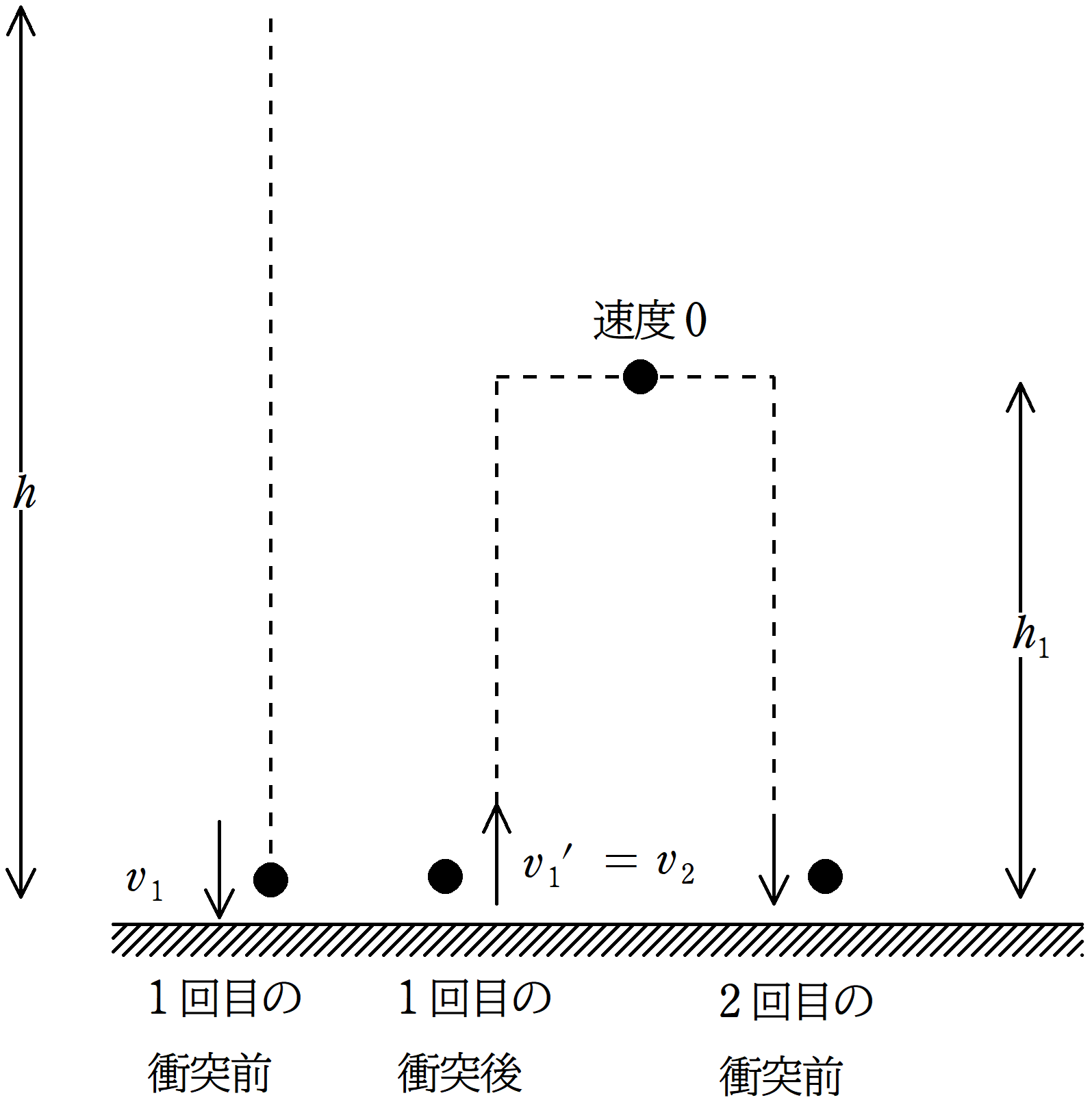
図のように,質量$m$の物体を水平でなめらかな床から高さ$h$の場所までもっていき,静かにはなした.物体と床とのはねかえり係数を$e(0<e<1)$とし,重力加速度の大きさを$g$として次の問いに答えよ.
(1) 物体が1回目の衝突をする直前の速さ$v_{1}$を求めよ.
(2) 物体を静かにはなしてから1回目の衝突をするまでの時間$t_{0}$を求めよ.
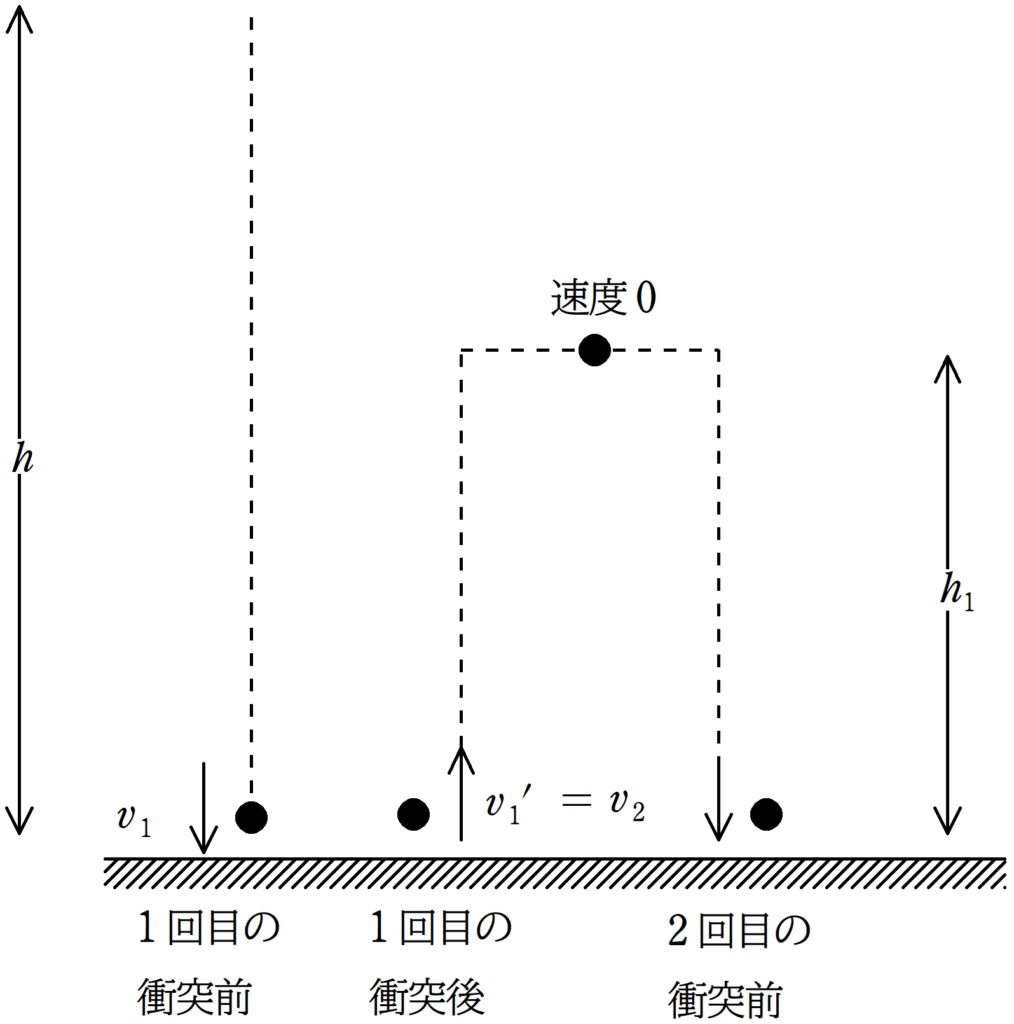
(3) 物体が1回目の衝突をした後,最高点に達した.このときの床からの高さ$h_{1}$を求めよ.
(4) $n$回目に床に衝突する直前の速さを$v_{n}$,衝突後の速さを$v_{n}^{\prime}$とする.このとき,$v_{n}^{\prime}$を$v_{n}$を用いて表せ.
(5) $n$回目の衝突直後の速さ$v_{n}^{\prime}$と$n+1$回目の衝突直前の速さ$v_{n+1}$は等しい.(4)より,$v_{n}$と$v_{n+1}$の関係式を導き,(1)の$v_{1}$の答えを用いて,$v_{n}$を$g$,$h$,$e$,$n$を用いて表せ.
(6) (5)と等加速度運動の式を用いて,$n$回目の衝突直後から最高点に達するまでの時間$t_{n}$を$g$,$h$,$e$,$n$を用いて表せ.
(7) $n$回目の衝突後に床から最高点に達したときの高さ$h_{n}$を$h$,$e$,$n$を用いて表せ.
<解答>

(1)から(3)は次の問題と同じなので,参考にしてください.
(1)
★ 力学的エネルギー保存則
$\dfrac{1}{2}mv_{1}^{2}+0=0+mgh$
$\therefore v_{1}=\sqrt{2gh}$ (答)
(2)
★ 等加速度運動の式
$h=\dfrac{1}{2}gt_{0}^{2}$
$\therefore t_{0}=\sqrt{\dfrac{2h}{g}}$ (答)
(3)
★ 力学的エネルギー保存則
$\eqalign{mgh_{1}&=\dfrac{1}{2}m(e\sqrt{2gh})^{2}\\&=e^{2}mgh\cr h_{1}&=e^{2}h}$ (答)
(4)

静止している壁や床との衝突の際には,衝突によって速さが$e$倍になります.
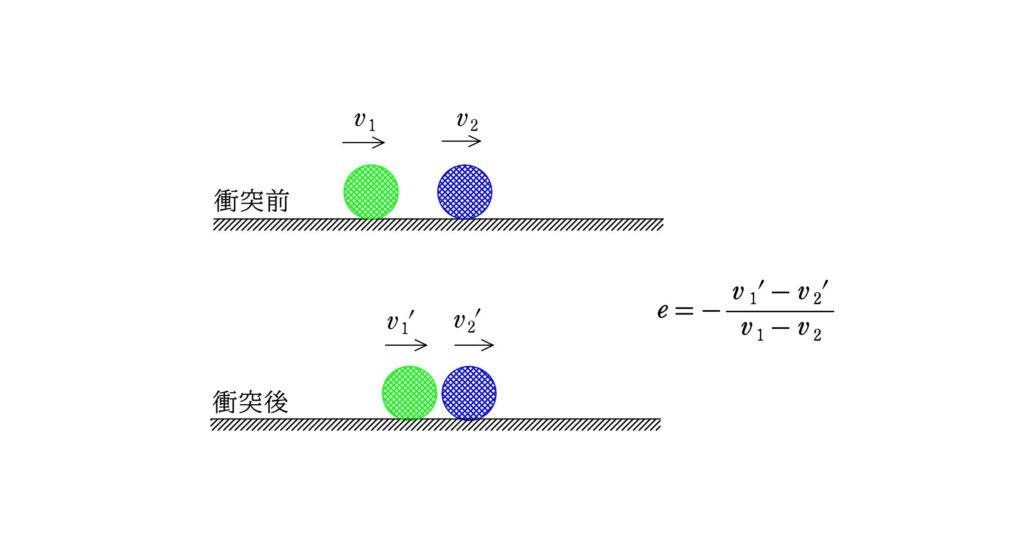
衝突前の物体の速度を$v_{1}$,$v_{2}$,衝突後の速度を$v_{1}^{\prime}$,$v_{2}^{\prime}$とするとき,はねかえり係数(反発係数)の式を次のように定義する.
$e=-\dfrac{v_{1}^{\prime}-v_{2}^{\prime}}{v_{1}-v_{2}}$
$e=1$のときを弾性衝突といい,力学的エネルギーが保存する.
また,$e=0$のときを完全非弾性衝突という.
★ はねかえり係数の式
$v_{n}^{\prime}=ev_{n}$ (答)
(5)

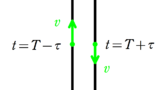
問題文にも書かれていますが,$v_{n}^{\prime}=v_{n+1}$です.投げあげ運動の際によく使うテクニックですね.
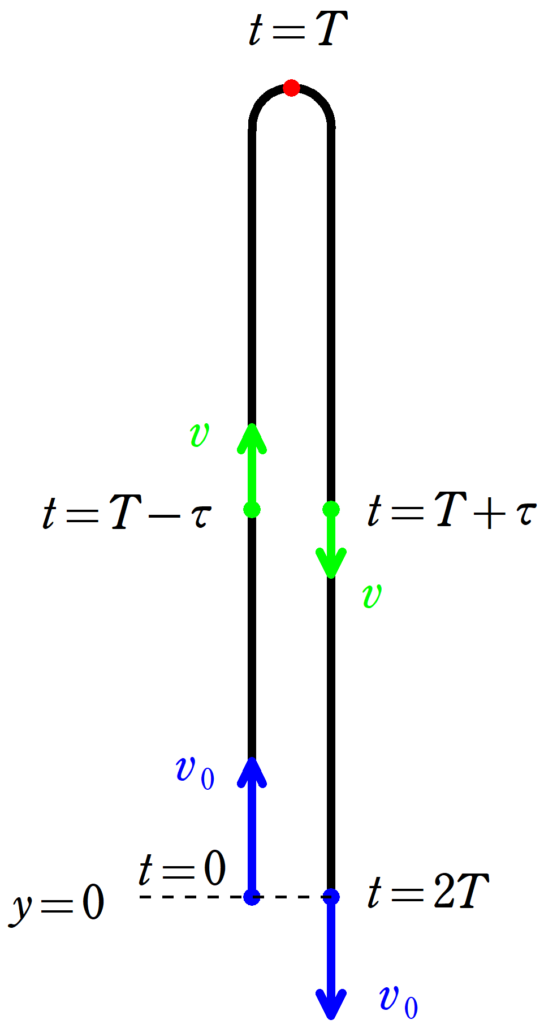
時刻$t=0$において,速さ$v_{0}$で投げ上げたときの運動を考える.
投げ上げた地点を原点として上向きに$y$座標をとる.
最高点に達する時刻を$T$とする.
時刻$t$における速度$v(t)$と座標$y(t)$について,次の関係が成り立つ.
運動$0\leqq \tau \leqq T$について
$|v(T-\tau)|=|v(T+\tau)|$
$y(T-\tau)=y(T+\tau)$
したがって
$v_{n+1}=ev_{n}$

これは,等比数列の漸化式だね.
初項が$v_{1}=\sqrt{2gh}$,公比が$e$(自然対数じゃなくて,反発係数だよ.)の等比数列です.
数列$\{a_{n}\}(n=1 , 2 , \dots)$について,$r$を実数として
$a_{n+1}=ra_{n}$
が成り立つとき,数列$\{a_{n}\}$は初項が$a_{1}$,公比が$r$の等比数列である.
等比数列の一般項は,
$a_{n}=a_{1}r^{n-1}$
$v_{n}=v_{1}e^{n-1}=e^{n-1}\sqrt{2gh}$ (答)
(6)

$n$回目の衝突直後の速度$v_{n}^{\prime}=e^{n}\sqrt{2gh}$の向きを正の方向とし,等加速度運動の式を立てます.
衝突直後から最高点(速度が$0$になる)に達するまでの時間を$t_{n}$として,等加速度運動の式より
★ 等加速度運動の式
$0=v_{n}^{\prime}-gt_{n}$
$t_{n}=\dfrac{e^{n}\sqrt{2gh}}{g}=e^{n}\sqrt{\dfrac{2h}{g}}$ (答)
(7)

力学的エネルギー保存則を用いて,$n$回目の衝突後の最高点の高さ$h_{n}$を求めましょう.
(等加速度運動の式でも求めることができます.)
★ 力学的エネルギー保存則
$mgh_{n}=\dfrac{1}{2}m(v_{n}^{\prime})^{2}$
$\therefore h_{n}=\dfrac{(v_{n}^{\prime})^{2}}{2g}$
(5)より,$v_{n}^{\prime}=e^{n}\sqrt{2gh}$であるから
$\eqalign{h_{n}=\dfrac{\{e^{n}\sqrt{2gh}\}^{2}}{2g}\\&=e^{2n}h}$ (答)


コメント