
今回の問題は,前回と同じく2つの物体の単振動です.
しかし,少し違うところがあります.
それは,片一方の物体がもう片一方の上にのっているというところです.
この場合は,相対運動を考えた方がわかりやすいです.
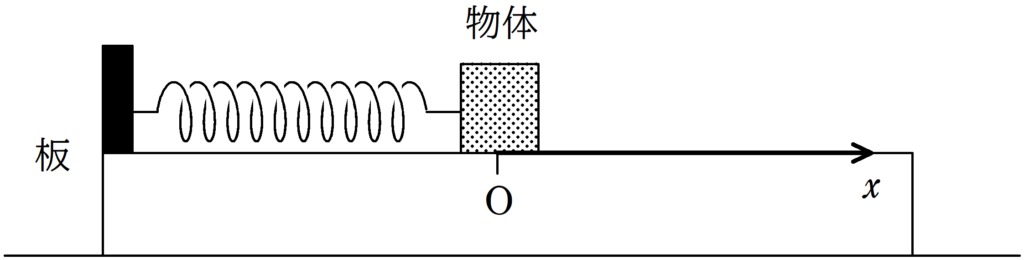
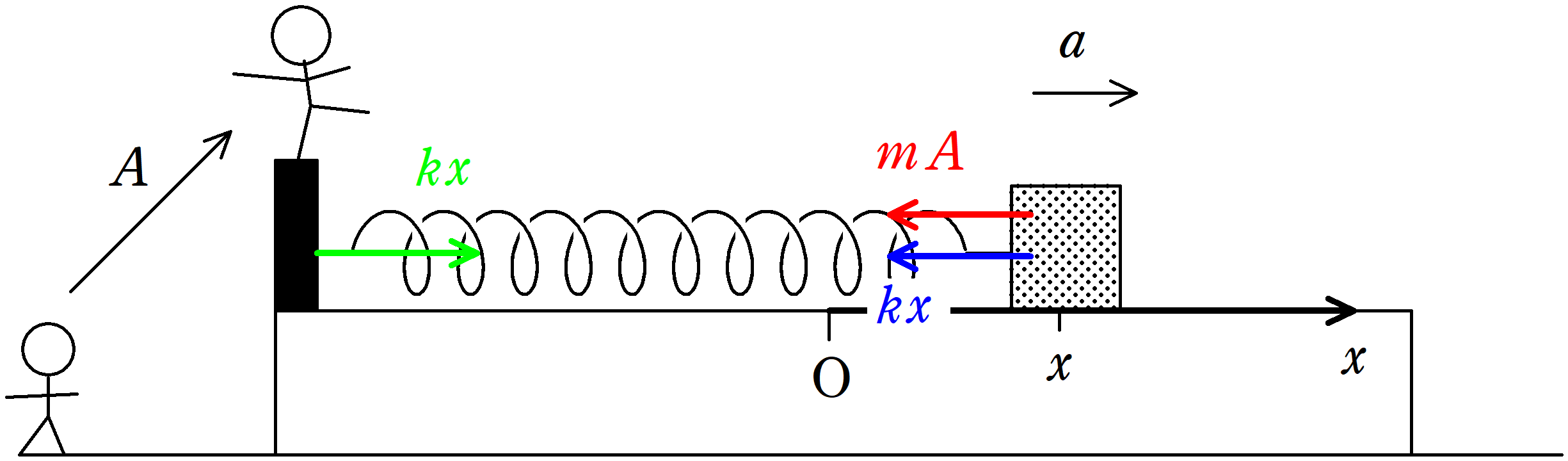
上図のように,水平でなめらかな床の上に,十分長い質量$M$の板をおく.
板の上には,質量$m$の物体がおかれており,ばね定数$k$の軽いばねによってつながれている.
ばねが自然長になるときの板の上の物体の位置を原点として,ばねが伸びる方向に板の上の目盛り$x$軸をとる.
ただし,水平な床と板,および,板と物体の間には摩擦力ははたらかない.
物体が原点にあるとき,時刻$t=0$で板に非常に短い時間で水平右方向に撃力を与え,板は大きさ$V_{0}$の初速度を得た.
このとき,次の問いに答えよ.
(1) 時刻$t$において,物体は板からみて座標$x$にあった.このときの物体の加速度を$a$として,板からみた物体の運動方程式を立てよ.ただし,板の加速度を$A$とする.
(2) (1)のとき,静止した座標からみた板の運動方程式を立て,$A$を$k$,$x$,$M$を用いて表せ.
(3) 板からみた物体の振動の周期を求めよ.
(4) 板からみた物体の振幅を求めよ.
(5) 板から見た時刻$t$における物体の速度$v(t)$を求めよ.
(6) 運動量が保存することを利用して,時刻$t$における板の速度$V(t)$を求めよ.
<解答>
(1)

板からみた物体の運動方程式です.
板自体が加速度をもっているので,板から物体をみると慣性力がはたらきますね.
加速度運動している観測者が物体をみたときに見かけの力がはたらく.
これを慣性力とよぶ.
観測者の加速度を$A$,物体の質量を$m$とすると,慣性力は
$m\cdot (-A)$
である.
つまり,観測者の加速度とは逆方向に大きさ$m|A|$の力がはたらく.
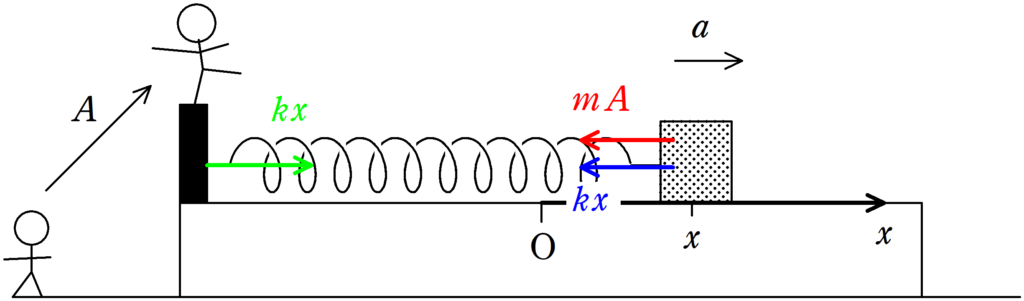
★ 板からみた物体の運動方程式
$ma=-kx-mA$ $\dots (\ast)$
(2)

板にはたらく水平方向の力は弾性力のみだね.
この弾性力は物体にはたらく弾性力の向きと逆だよ.
★ 板の運動方程式
$MA=kx$
$\therefore$ $A=\dfrac{kx}{M}$ $\dots (2\ast)$
(3)

$(2\ast)$を$(\ast)$に代入すると,単振動運動方程式の形を得るよ.
$(2\ast)$を$(\ast)$に代入して
$ma=-kx-m\cdot \dfrac{k}{M}=-\dfrac{M+m}{M}kx$

この運動方程式から,振動の中心は$x=0$,角振動数$\omega$は
$\omega=\sqrt{\dfrac{M+m}{Mm}k}$
そして,周期$T$は
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{Mm}{(M+m)k}}$
したがって,周期は$T=2\pi\sqrt{\dfrac{Mm}{(M+m)k}}$です.
(4)

板からみた物体の振幅を調べます.
まず,板からみた物体の初速度は$-V_{0}$です.
次の図で確認しましょう.
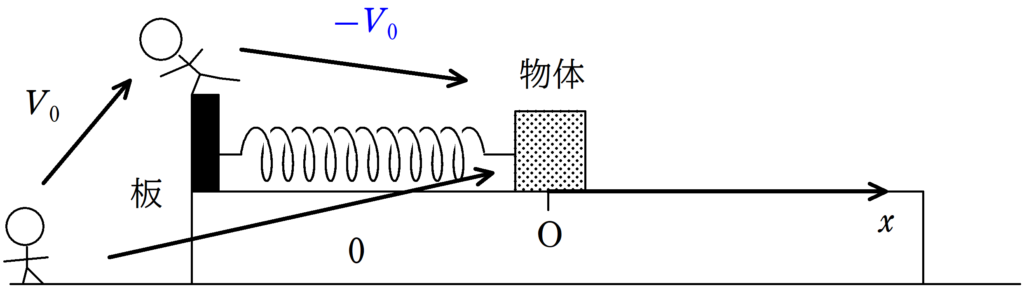

すると,板からみて物体は,振動の中心からスタートして負の方向にいくので,$-\sin$型ですね.
振幅を$C$とおくと,板からみた物体の振動の式は次のように表すことができます.
$x=-C\sin\sqrt{\dfrac{M+m}{Mm}k}t$
時間$t$で微分すると,速度$v(t)$は
$v(t)=\dfrac{dv(t)}{dt}=-C\sqrt{\dfrac{M+m}{Mm}k}\cos\sqrt{\dfrac{M+m}{Mm}k}t$ $\dots (3\ast)$
初期条件,$v(0)=-V_{0}$を代入して
$-V_{0}=-C\sqrt{\dfrac{M+m}{Mm}k}$
$\therefore$ $C=V_{0}\sqrt{\dfrac{Mm}{(M+m)k}}$
したがって,振幅$C$は$C=V_{0}\sqrt{\dfrac{Mm}{(M+m)k}}$
(5) さらに(4)で得た振幅$C$を$(3\ast)$に代入して
$\eqalign{v(t)&=-V_{0}\sqrt{\dfrac{Mm}{(M+m)k}}\cdot \sqrt{\dfrac{M+m}{Mm}k}\cos\sqrt{\dfrac{M+m}{Mm}k}t\\&=-V_{0}\cos\sqrt{\dfrac{M+m}{Mm}k}t}$
したがって,$v(t)==-V_{0}\cos\sqrt{\dfrac{M+m}{Mm}k}t$
(6)

最後に,板と物体は撃力を与えられた後では,水平方向にはたらく力の和が0なので,運動量が保存します.
$t=0$と任意の時刻における運動量保存の式を立てましょう.
ただし,運動量保存則は原則として,静止した座標からの速度を用いてくださいね.
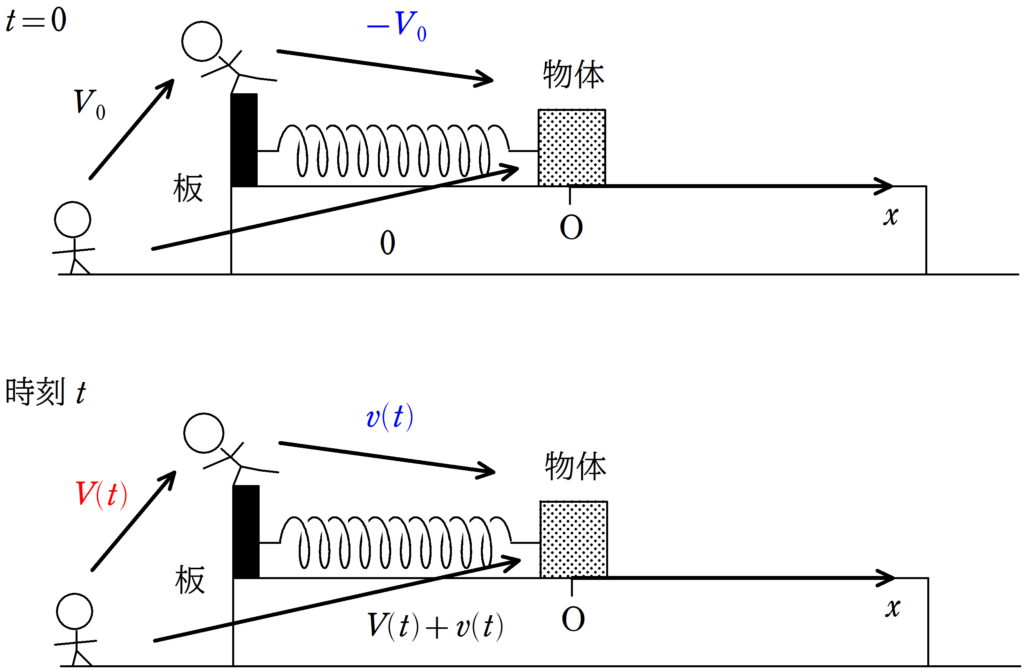
★ 運動量保存則
時刻$t$における板の速度を$V(t)$とすると,運動量保存則より
$\eqalign{MV_{0}+m\cdot 0 &=MV(t)+m\{V(t)+v(t)\}\cr (M+m)V(t)&=MV_{0}-mv(t)\cr V(t)&=\dfrac{MV_{0}-mv(t)}{M+m}}$
(5)で得た$v(t)=-V_{0}\cos\sqrt{\dfrac{M+m}{Mm}k}t$を代入して
$V(t)=\dfrac{(M+m\cos\sqrt{\dfrac{M+m}{Mm}k}t)V_{0}}{M+m}$

以上でおしまいです!



コメント