
前回は,重心が静止していたときの単振動の問題を扱いました.
今回は,重心自体がうごきつつ,重心からみた単振動を考えていきます.
前回の内容はこちら
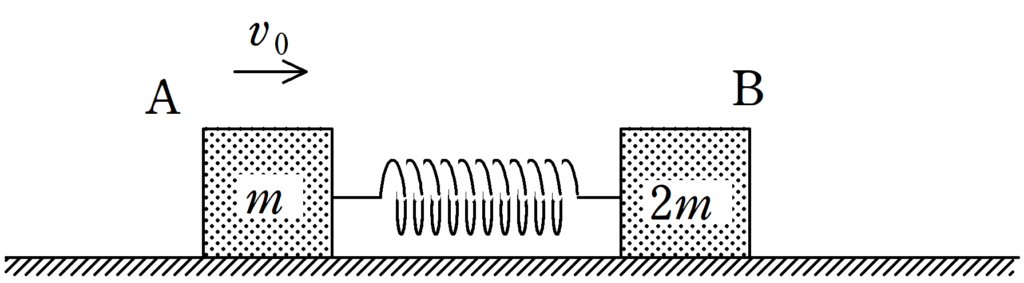
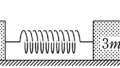
図のように,水平で滑らかな床の上に,質量$m$,$2m$の物体がA,Bがばね定数$k$のばねによってつながれている.
はじめ,ばねは自然長の状態でAとBは静止している.
この状態から時刻$t=0$でAに瞬間的に力を加えて,大きさ$v_{0}$の初速度を図の向きに与えた.
このとき,次の問いに答えよ.
ただし,図の水平右向きを正とする.
(1) 時刻$t=0$における重心速度を求めよ.
(2) 重心からみた物体Bの単振動を周期を求めよ.
(3) 重心からみたBの振動の振幅を求めよ.
<解答>

重心速度の定義をまとめておこう!
速度$v_{1}$,$v_{2}$をもつ質量$m_{1}$,$m_{2}$の物体がある.
このときの重心速度$v_{\rm G}$は
$v_{\rm G}=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}$

$t=0$のときのAの速度が$v_{0}$,Bの速度が0だから,重心の初速度$v_{\rm G0}$は次のようになるね.
$v_{\rm G0}=\dfrac{mv_{0}+2m\cdot 0}{m+2m}=\dfrac{1}{3}v_{0}$
したがって,答えは$v_{\rm G0}=\dfrac{1}{3}v_{0}$.
(2)

次に,ばね定数はばねの長さに反比例することを用いて,重心からみたA側のばね定数$k_{\rm A}$とB側のばね定数$k_{\rm B}$を計算してみよう.
ちなみに,重心は線分ABを$2:1$に内分した場所にあることがわかるね.
★ A側のばね定数
$k:k_{\rm A}=1:\dfrac{1}{\dfrac{2}{3}}$
$\therefore$ $k_{\rm A}=\dfrac{3}{2}k$
★ B側のばね定数
$k:k_{\rm B}=1:\dfrac{1}{\dfrac{1}{3}}$
$\therefore$ $k_{\rm B}=3k$
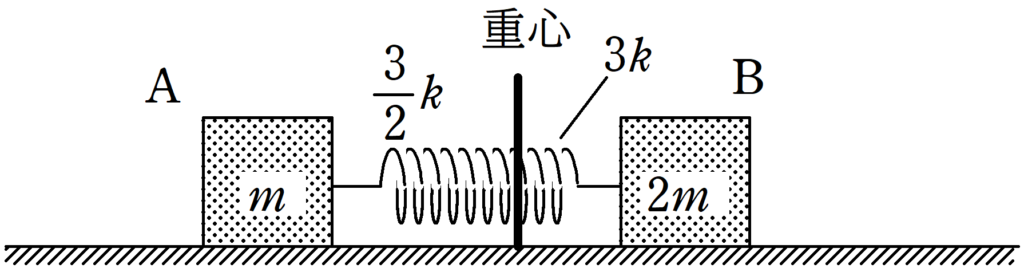

それでは,重心からみたBの運動を解析しましょう.
運動方程式を立てる前に,重心からみたAとBの初速度$v_{\rm GA}$と$v_{\rm GB}$を調べておきましょう.
重心速度が(1)より,$v_{\rm G0}=\dfrac{1}{3}v_{0}$であることを用います.
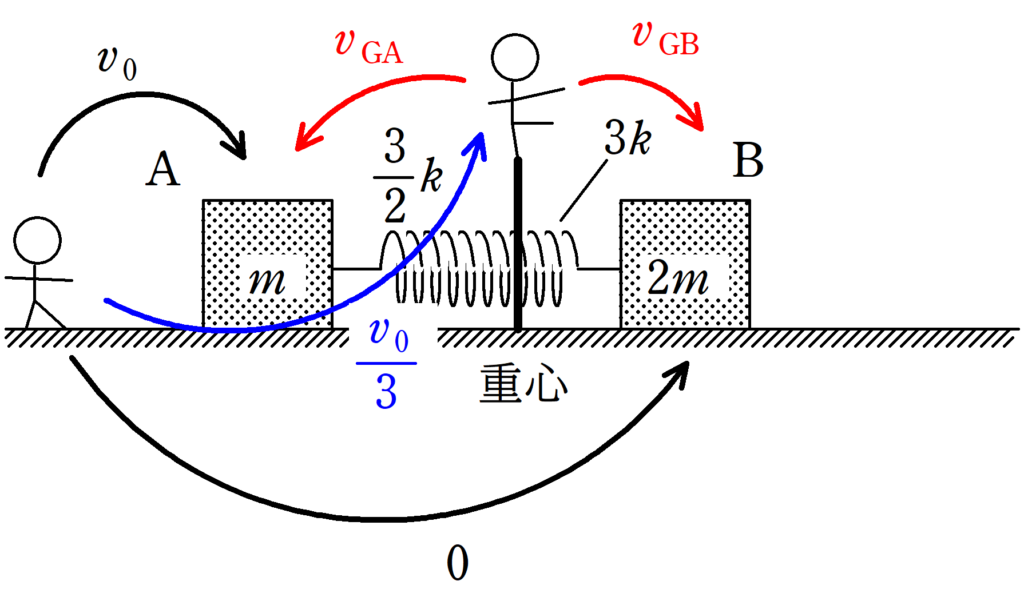
★ 重心からみたAの相対初速度
$\dfrac{1}{3}v_{0}+v_{\rm GA}=v_{0}$ $\therefore v_{\rm GA}=\dfrac{2}{3}v_{0}$
★ 重心からみたBの相対初速度
$\dfrac{1}{3}v_{0}+v_{\rm GB}=0$ $\therefore v_{\rm GB}=-\dfrac{1}{3}v_{0}$

一応,確認しておくと,
$m\cdot \dfrac{2}{3}v_{0}+2m\cdot (-\dfrac{1}{3}v_{0})=0$
となっているので,重心からみた運動量の和は0となっています.
質量$m_{1}$,$m_{2}$の物体がある.
重心からみたそれぞれの速度を$v_{\rm G1}$,$v_{\rm G2}$とすると,次の式が成り立つ.
$m_{1}v_{\rm G1}+m_{2}v_{\rm G2}=0$
すなわち,重心からみた物体の運動量の和は0となる.

さて,重心からみたBの運動方程式を立てましょう.
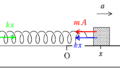
自然長の位置を原点として,ばねが伸びる方向に$x_{\rm B}$軸をとります.
位置$x_{\rm B}$における加速度を$a_{\rm B}$としましょう.
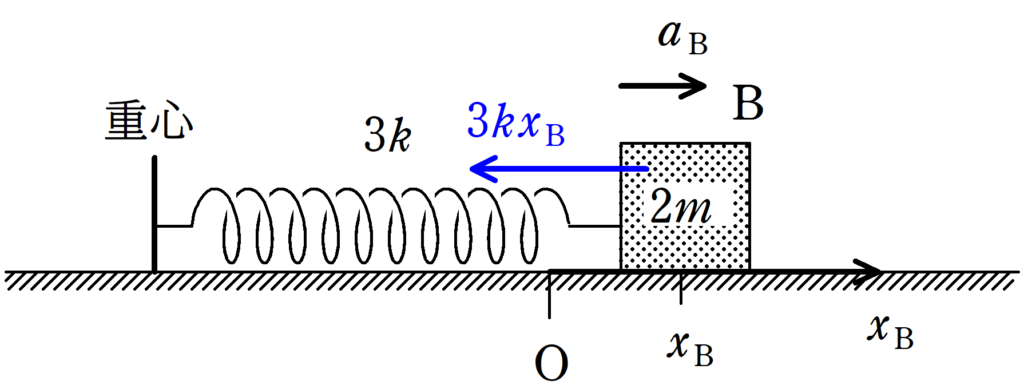
★ 重心からみたBの運動方程式
$2ma_{\rm B}=-3kx_{\rm B}$

したがって,振動の中心は原点(自然長の位置),角振動数$\omega_{\rm B}$と振動の周期$T_{\rm B}$はそれぞれ
$\omega_{\rm B}=\sqrt{\dfrac{3k}{2m}}$
$T_{\rm B}=\dfrac{2\pi}{\omega_{\rm B}}=2\pi\sqrt{\dfrac{2m}{3k}}$
したがって,答えは,$T_{\rm B}=2\pi\sqrt{\dfrac{2m}{3k}}$です.
(3)

今回は,振幅を次の2通りの方法で求めましょう.
$\clubsuit$方法1$\clubsuit$ 速度の時間変化の利用
重心からみたBの振幅を$|A|$とします.
すると,時刻$t$における位置$x_{\rm B}$は
$\eqalign{x_{\rm B}&=A\sin\omega_{\rm B}t\\&=A\sin\sqrt{\dfrac{3k}{2m}}t}$
この式を$t$で微分して時刻$t$における速度$v_{\rm B}$を計算すると
$v_{\rm B}=A\sqrt{\dfrac{3k}{2m}}\cos\sqrt{\dfrac{3k}{2m}}t$ $\dots (\ast)$
ここで,初期条件$t=0$のとき,$v_{\rm B}=v_{\rm GB}=-\dfrac{1}{3}v_{0}$より
$-\dfrac{1}{3}v_{0}=A\sqrt{\dfrac{3k}{2m}}\cdot 1$
$\therefore$ $A=-\dfrac{1}{3}v_{0}\sqrt{\dfrac{2m}{3k}}$
したがって,振幅は$|A|=\dfrac{1}{3}v_{0}\sqrt{\dfrac{2m}{3k}}$
ちなみに,$A=-\dfrac{1}{3}v_{0}\sqrt{\dfrac{2m}{3k}}$を$(\ast)$に代入して
$\eqalign{v_{\rm B}&=-\dfrac{1}{3}v_{0}\sqrt{\dfrac{2m}{3k}}\cdot \sqrt{\dfrac{3k}{2m}}\cos\sqrt{\dfrac{3k}{2m}}t\\&=-\dfrac{1}{3}v_{0}\cos\sqrt{\dfrac{3k}{2m}}t}$
を得る.
$\clubsuit$方法2$\clubsuit$ 単振動のエネルギー保存の利用
質量$m$の物体の位置$x$における加速度を$a$とする.
また,定数$x_{0}$と正の定数$k$を用いて,運動方程式が
$ma=-k(x-x_{0})$
となるとき,この運動方程式を変形して
$\dfrac{1}{2}mv^{2}+\dfrac{1}{2}k(x-x_{0})^2=$一定
が成り立つ.ただし,$v$は速さである.
重心からみたBの運動方程式
$2ma_{\rm B}=-3kx_{\rm B}$
より,単振動のエネルギー保存
$\dfrac{1}{2}\cdot 2m v_{\rm B}^{2}+\dfrac{1}{2}\cdot 3k x_{\rm B}^{2}=$一定
が成り立つ.
振動の中心と振動の端でこの保存則を適用する.
振幅を$A$として
$\eqalign{\dfrac{1}{2}\cdot 2m\cdot (-\dfrac{1}{3}v_{0})^{2}+\dfrac{1}{2}\cdot 3k \cdot 0^{2}&=\dfrac{1}{2}\cdot 2m \cdot 0^{2}+\dfrac{1}{2}\cdot 3kA^{2}\cr A^{2}&=\dfrac{2m}{3k}\cdot (\dfrac{1}{3}v_{0})^{2} \cr A&=\dfrac{1}{3}v_{0} \sqrt{\dfrac{2m}{3k}}}$
したがって,振幅は$\dfrac{1}{3}v_{0} \sqrt{\dfrac{2m}{3k}}$となります.

問題は以上になりますが,最後に物体Aと物体Bが時間とともにどのように移動していくのかを調べましょう.
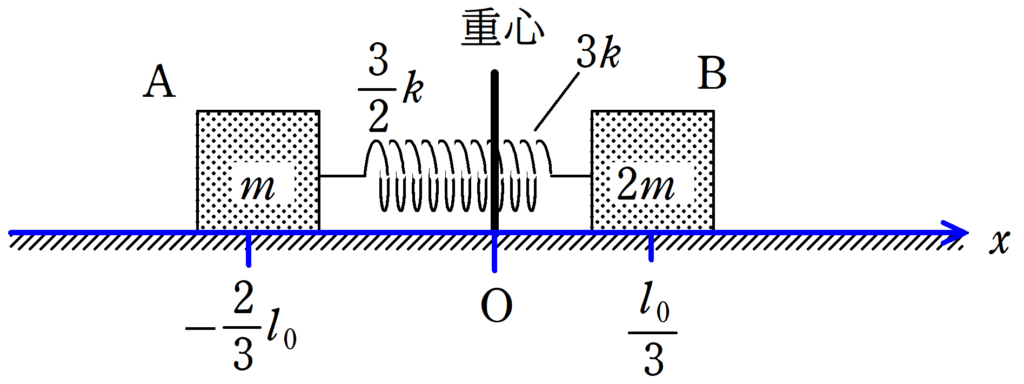

上図のように,$t=0$における重心の位置を原点として,ばねお自然の長さ
を$l_{0}$としましょう.
すると,AとBの初期位置は$-\dfrac{2}{3}l_{0}$,$\dfrac{1}{3}l_{0}$です.
AとBにはたらく水平方向の力の和は0なので,重心加速度は0です.
したがって,重心は速度$\dfrac{1}{3}v_{0}$で等速直線運動します.
一方,重心からみたBの振動は今までの考察から
$-\dfrac{1}{3}v_{0}\sqrt{\dfrac{2m}{3k}}\sin\sqrt{\dfrac{3k}{2m}}t$
となるので,Bの時刻$t$における位置$x_{\rm B}(t)$は
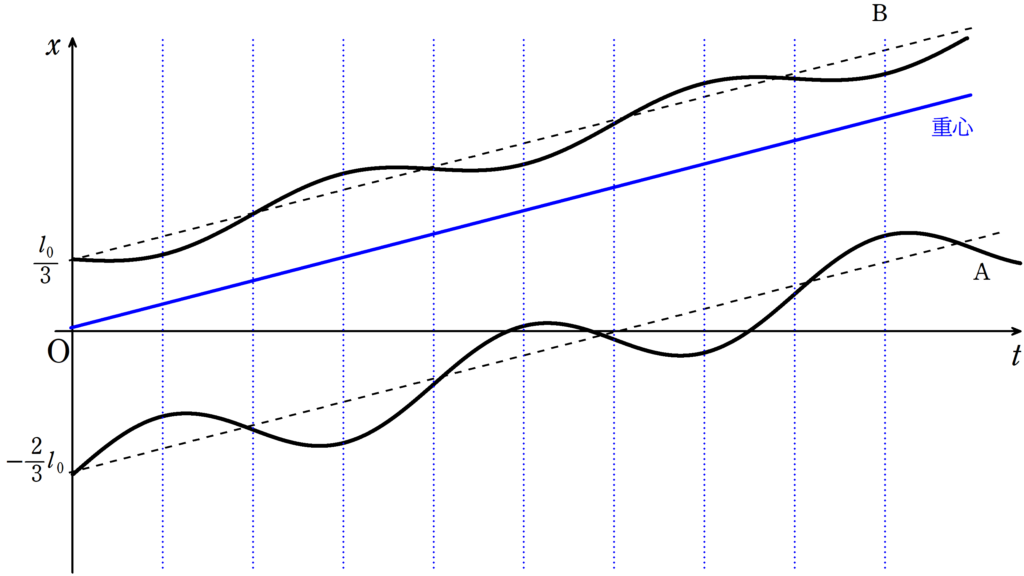
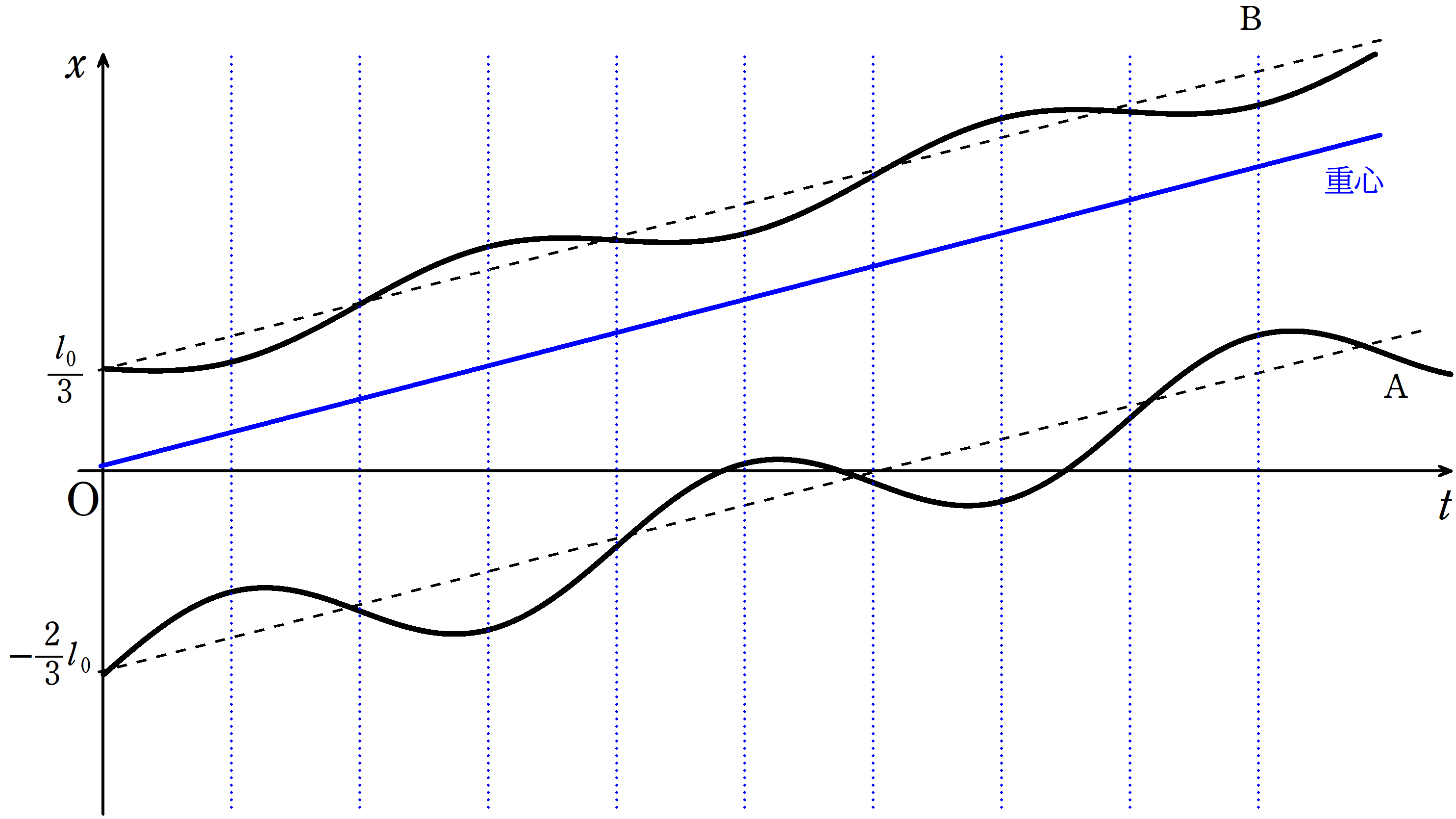
$x_{\rm B}(t)=\dfrac{1}{3}l_{0}+\dfrac{1}{3}v_{0}t-\dfrac{1}{3}v_{0}\sqrt{\dfrac{2m}{3k}}\sin\sqrt{\dfrac{3k}{2m}}t$
となります.

重心の等速直線運動+単振動の形になっているね!

Aも同様に考えていけば
$x_{\rm A}=-\dfrac{2}{3}l_{0}+\dfrac{1}{3}v_{0}t+\dfrac{2}{3}v_{0}\sqrt{\dfrac{2m}{3k}}\sin\sqrt{\dfrac{3k}{2m}}t$
となり,$x-t$グラフは次のようになります.

コメント
[…] […]