
2021年の東北大の前期試験で波の式からドップラー効果の説明をする問題が出たね.
今回は,波の式による観測者が観測する振動数の3つパターンを解説します!
図1から図3のように,時刻$0$で音源は原点Oにあり,観測者が$x_{0}$にいる.音源は時刻$t$において,$y_{0}=A\sin(2\pi ft)$で振動している.ただし,$A$は振幅でであり,$f$は振動数である.また,$A , f>0$であり,音が伝わる速さを$V$とする.このとき,以下の問いに答えよ.
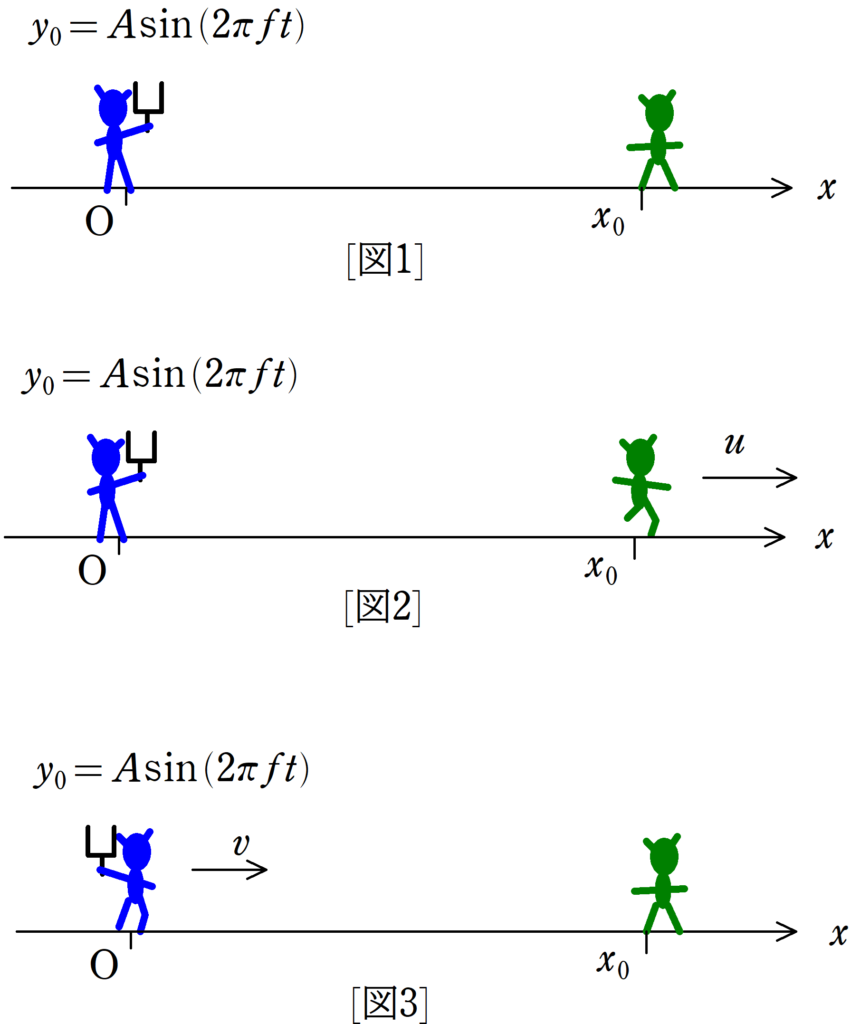
(1) 音源も観測者も静止している場合を考える.[図1]
(1.1)音源から出した音が観測者に届くのにかかる時間はどれほどか.$V,x_{0}$を用いて表せ.
(1.2)時刻$t$における観測者がいる場所($x=x_{0}$)の媒質の変位の式$y_{1}$を$A$,$f$,$V$,$x_{0}$,$t$を用いて表せ.
(1.3)(1.2)において,時刻$t$における位相から時刻$t+\varDelta t$における位相が$2\pi$変化したときの$\varDelta t$を求めよ.また,$\dfrac{1}{\varDelta t}$が観測者が観測する振動数であることから,観測者が観測する振動数が$f$であることを確かめよ.
(2) 音源が静止し,観測者が$x$軸の正方向に一定の速さ$u$で音源から遠ざかっている場合を考える.[図2]
(2.1) 観測者が時刻$t$において波を受け取った.この波は,どれほど前に音源が出した波であったか.$x_{0}$,$u$,$t$,$V$を用いて表せ.
(2.2) 時刻$t$における観測者がいる場所の媒質の変位の式$y_{2}$を$A$,$f$,$V$,$u$,$x_{0}$,$t$を用いて表せ.
(2.3) (2.2)において,時刻$t$における位相から時刻$t+\varDelta t$における位相が$2\pi$変化したときの$\varDelta t$を求めよ.また,$\dfrac{1}{\varDelta t}$が観測者が観測する振動数であることから,観測者が観測する振動数$f_{2}$を$V$,$u$,$f$を用いて表せ.
(3) 音源が一定の速さ$v$で観測者に向かっていき,観測者が静止している場合を考える.[図3]
(3.1) 時刻$t_{0}$に音源から出した音が観測者に届く時刻$t$とする.$t_{0}$を$V$,$v$,$t$,$x_{0}$を用いて表せ.
(3.2) 時刻$t$における観測者がいる場所($x=x_{0}$)の媒質の変位の式$y_{3}$を$A$,$f$,$V$,$v$,$x_{0}$,$t$を用いて表せ.
(3.3) (3.2)において,時刻$t$における位相から時刻$t+\varDelta t$における位相が$2\pi$変化したときの$\varDelta t$を求めよ.また,$\dfrac{1}{\varDelta t}$が観測者が観測する振動数であることから,観測者が観測する振動数$f_{3}$を$V$,$v$,$f$を用いて表せ.
<解答>

1回振動するのにかかる時間が周期$T$であり,その逆数$\dfrac{1}{T}$が振動数です.
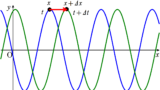
横軸が時間$t$で縦軸が媒質の変位$y$の次のグラフを見てください.
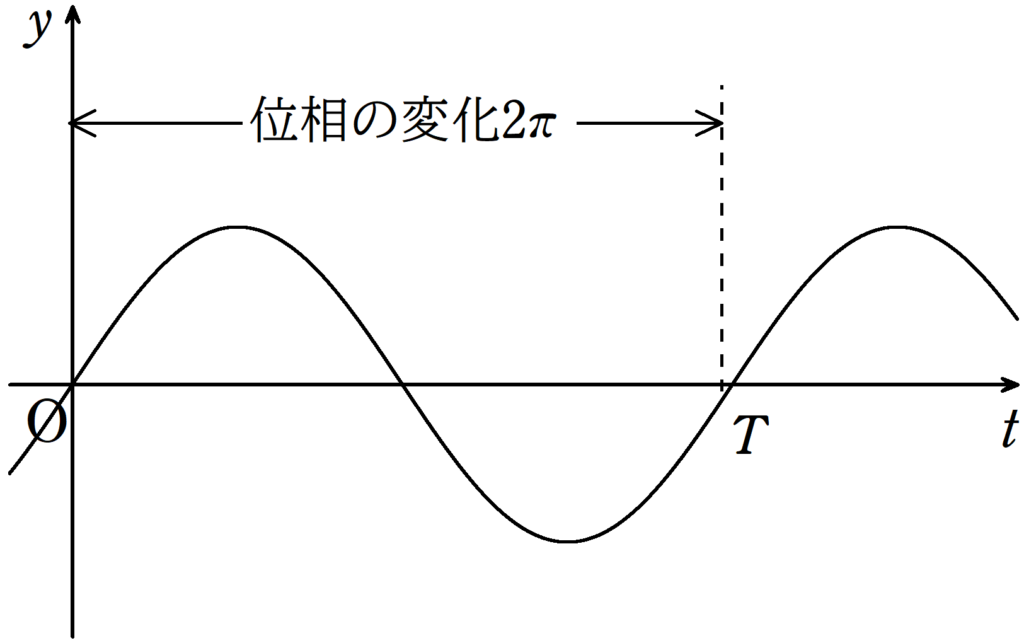

時間$T$(周期)分の位相の変化が$2\pi$です.
このことを使って問題を解いていきます.
ちなみに,位相の変化と周期の問題として,こちらの問題も参考にしてください.
(1)
(1.1)

音が伝わる速さは$V$で,音源から観測者までの距離は$x_{0}$です.
したがって,音源から観測者に音が伝わる時間は$\dfrac{x_{0}}{V}$(答)です.
(1.2)

波の式についてはこちらでも説明しています.
観測者がいる場所の振動は,時間$\dfrac{x_{0}}{V}$前の原点(音源)での振動と同じです.
$y_{1}=A\sin\left\{2\pi f\left(t-\dfrac{x_{0}}{V}\right)\right\}$ (答)
(1.3)

(1.2)で得た式の位相($\sin$の中の部分)を時間によって変化する部分と変化しない部分に分けてみましょう.
★ 位相
$2\pi ft-\dfrac{2\pi fx_{0}}{V}$
$\phi_{1}=\dfrac{2\pi fx_{0}}{V}$として
$2\pi ft-\phi_{1}$

時刻$t$での位相と時刻$t+\varDelta t$の位相の変化が$2\pi$であるときの$\varDelta t$を求めましょう.
$\left\{2\pi f(t+\varDelta t)-\cancel{\phi_{1}}\right\}-\left\{2\pi ft-\cancel{\phi_{1}}\right\}=2\pi$
$\therefore \varDelta t=\dfrac{1}{f}$ (答)

$\varDelta t$は振動の周期で,その逆数が振動数$f_{1}$です.
$f_{1}=\dfrac{1}{\varDelta t}=f$ (答)
(2)
(2.1)

時刻$t$において,観測者は時刻$0$の位置から$ut$だけ移動しています.
なので,音が伝わった距離は,$x_{0}+ut$であり,この距離を音が伝えるのにかかる時間$t_{2}$は,次の関係式により求めることができます.
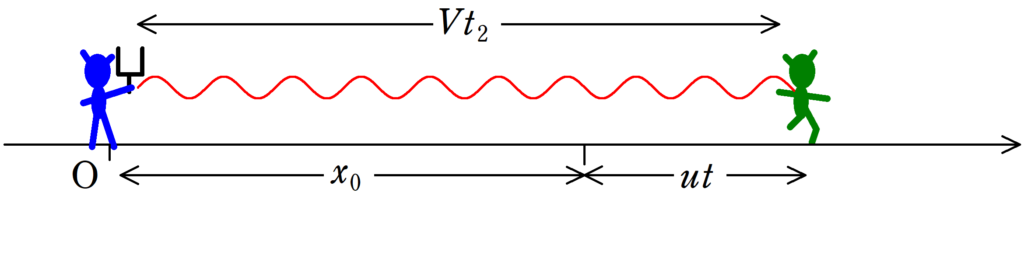
$Vt_{2}=x_{0}+ut$
$\therefore t_{2}=\dfrac{x_{0}+ut}{V}$ (答)
(2.2)

(2.1)より,時刻$t$において,観測者が受け取った波は,時刻$t-\dfrac{x_{0}+ut}{V}$に音源が出した波と位相が一緒です.
$y_{2}=A\sin\left\{2\pi f\left(t-\dfrac{x_{0}+ut}{V}\right)\right\}$ (答)
(2.3)

同様に,(2.2)で得た式の位相部分を$t$によって変化する項と定数項に分けます.
★ 位相
$\dfrac{2\pi f(V-u)}{V}t-\dfrac{2\pi fx_{0}}{V}$
$\phi_{2}=\dfrac{2\pi fx_{0}}{V}$とすると
$\dfrac{2\pi f(V-u)}{V}t-\phi_{2}$

時刻$t$での位相と時刻$t+\varDelta t$の位相の変化が$2\pi$であるときの$\varDelta t$を求めましょう.
$\left\{\dfrac{2\pi f(V-u)}{V}(t+\varDelta t)-\cancel{\phi_{2}}\right\}-\left\{\dfrac{2\pi f(V-u)}{V}t-\cancel{\phi_{2}}\right\}=2\pi$
$\therefore \varDelta t=\dfrac{V}{f(V-u)}$
したがって,求める振動数$f_{2}$は
$f_{2}=\dfrac{1}{\varDelta t}=\dfrac{V-u}{V}f$ (答)
(3)
(3.1)
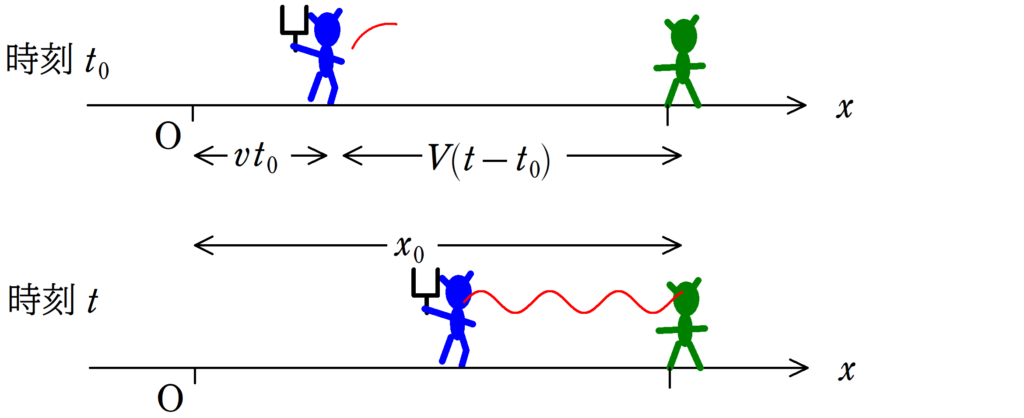

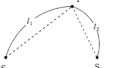
上図をみてみましょう.
時刻$t_{0}$では音源は$vt_{0}$だけ移動しています.
すると,この時点で音源と観測者の距離は$x_{0}-vt_{0}$となります.
時刻$t$には観測者に届いているので,音が伝わる時間は$t-t_{0}$となります.
$V(t-t_{0})=x_{0}-vt_{0}$
$\therefore t_{0}=\dfrac{V}{V-v}t-\dfrac{x_{0}}{V-v}$ (答)
(3.2)

時刻$t$で観測者が受け取った媒質の振動は,時刻$t_{0}$で音源が出した振動と同じです.
$y_{3}=A\sin\left\{2\pi f\left(\dfrac{V}{V-v}t-\dfrac{x_{0}}{V-v}\right)\right\}$ (答)
(3.3)

今回も位相部分を$t$によって変化する項と定数項に分けます.
★ 位相
$2\pi f\left(\dfrac{V}{V-v}t-\dfrac{x_{0}}{V-v}\right)=\dfrac{2\pi fV}{V-v}t-\dfrac{2\pi fx_{0}}{V-v}$
$\phi_{3}=\dfrac{2\pi fx_{0}}{V-v}$として
$\dfrac{2\pi fV}{V-v}t-\phi_{3}$

時刻$t$での位相と時刻$t+\varDelta t$の位相の変化が$2\pi$であるときの$\varDelta t$を求めましょう.
$\left\{\dfrac{2\pi fV}{V-v}(t+\varDelta t)-\cancel{\phi_{3}}\right\}-\left\{\dfrac{2\pi fV}{V-v}t-\cancel{\phi_{3}}\right\}=2\pi$
$\therefore \varDelta t=\dfrac{V-v}{Vf}$
したがって,求める振動数$f_{3}$は
$f_{3}=\dfrac{1}{\varDelta t}=\dfrac{V}{V-v}f$ (答)




コメント
[…] 波の式(位相)によるドップラー効果の説明 […]