
前回の内容はこちらです.
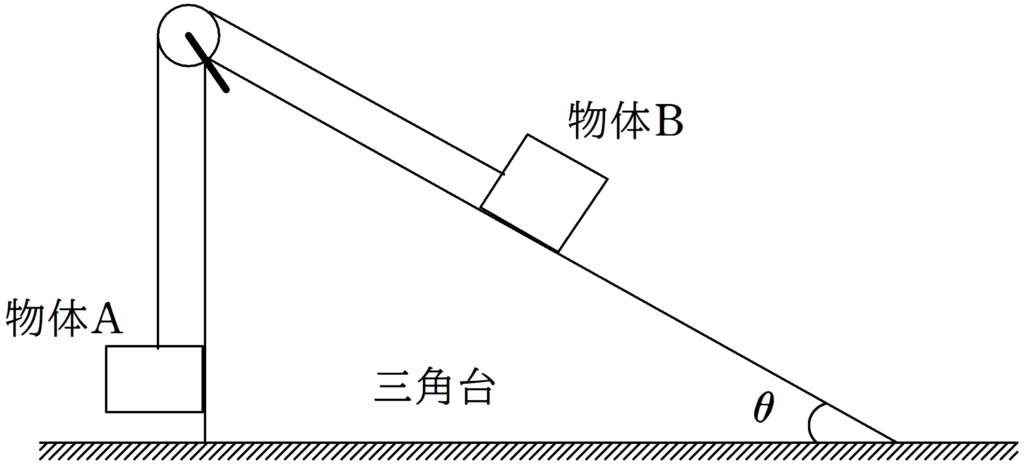
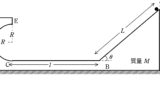
図のように,水平でなめらかな床の上に質量$M_{3}$の三角台がおいてある.三角台の上面は傾角$\theta$の斜面でできており,斜面はなめらかである.斜面の上には質量$M_{2}$の物体Bが置かれており,物体Bは質量の無視できる糸で結ばれており,糸は質量の無視できる滑車を通じて質量$M_{1}$の物体Aにつながれている.物体Aは常に三角台と接触できる構造になっていて,なめらかに三角台の鉛直面を動く.物体A,物体B,三角台がすべて静止した状態から静かに手をはなすと,物体A,物体B,三角台は運動をはじめた.物体Bが斜面上を$l$だけ下ったときに,三角台はどれだけ移動したか.ただし,物体A,物体B,三角台は同一平面内を動くとする.
<解答>
はじめ,重心が静止していて,その後,ある成分について力の和が0であるとき,その成分の重心は静止したままである.

今回も水平方向にはたらく力の和は0です.
したがって,重心は変化しません.
今回のポイントは,物体Aと三角台の水平方向の変位が同じであるということです.

変位を利用した重心不変は次の2式を立てましょう.
重心不変の条件を満たすとき,次の2式を立てる.
1. 重心不変の式,つまり,重心の変化が0である式を立てる.
2. 相対変位の式
★ 重心不変の式
床からみた三角台と物体Aの水平方向の変位を$\varDelta X$(求めたいもの),物体Bの水平方向の変位を$\varDelta x$とすると
$0=\dfrac{M_{1}\varDelta X+M_{2}\varDelta x+M_{3}\varDelta X}{M_{1}+M_{2}+M_{3}}$
$\therefore \varDelta x=-\dfrac{M_{1}+M_{3}}{M_{2}}\varDelta X$ $\dots (\ast)$
★ 相対変位の式
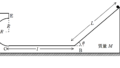
下図を参考にして(※下図はそれぞれ水平方向の変位を表している.)
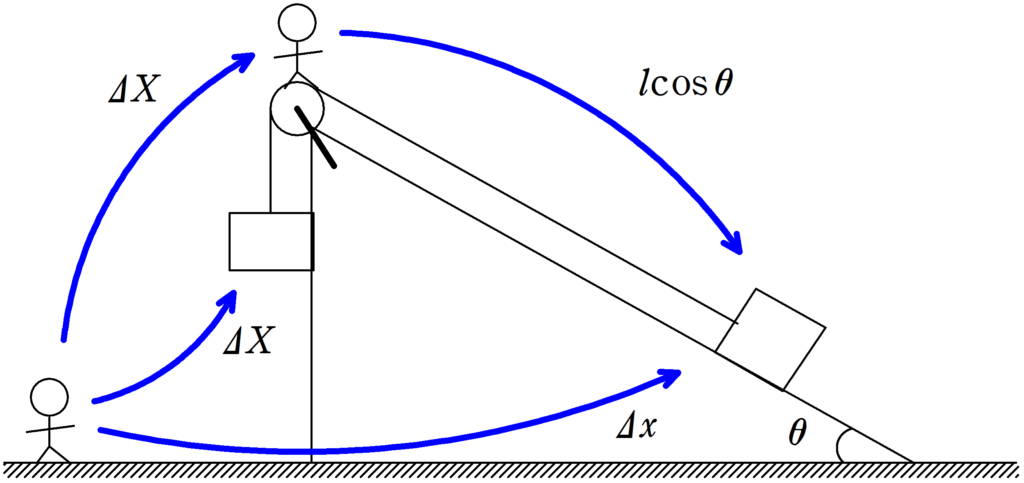
$\varDelta X+l\cos\theta=\varDelta x$ $\dots (2\ast)$
$(\ast)$,$(2\ast)$より
$\eqalign{\varDelta X+l\cos\theta&=-\dfrac{M_{1}+M_{3}}{M_{2}}\varDelta X\cr\dfrac{M_{1}+M_{2}+M_{3}}{M_{2}}\varDelta X&=-l\cos\theta\cr\varDelta X=-\dfrac{M_{2}l\cos\theta}{M_{1}+M_{2}+M_{3}}}$

したがって,三角台は図の左向きに$\dfrac{M_{2}l\cos\theta}{M_{1}+M_{2}+M_{3}}$(答)です.

次回の内容はこちらです.

コメント
[…] […]
[…] […]