
引き続き,$pV$グラフを読み取る演習しましょう.
まず,確認してほしいのが,次の2つです!
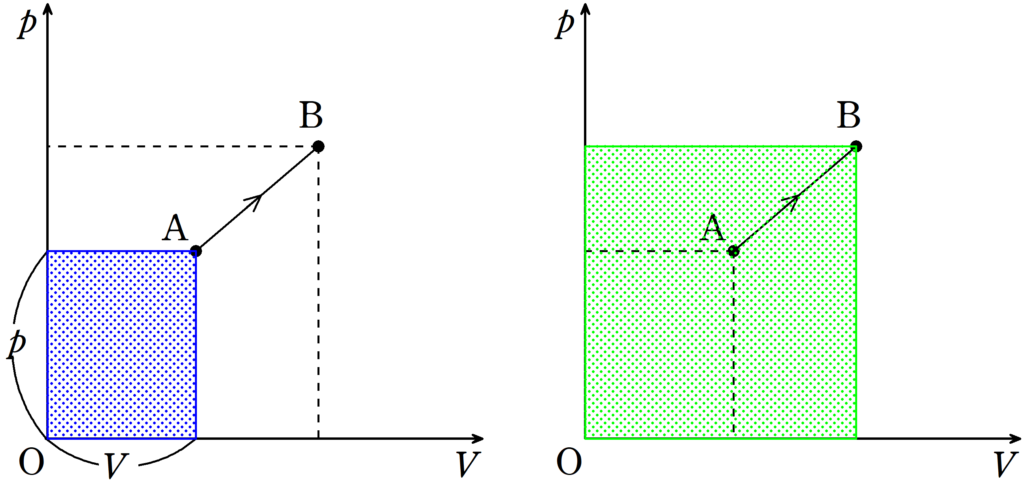
絶対温度は状態の点から$p$軸$V$軸へ下した垂線の足と原点でつくられる長方形の面積に比例する.
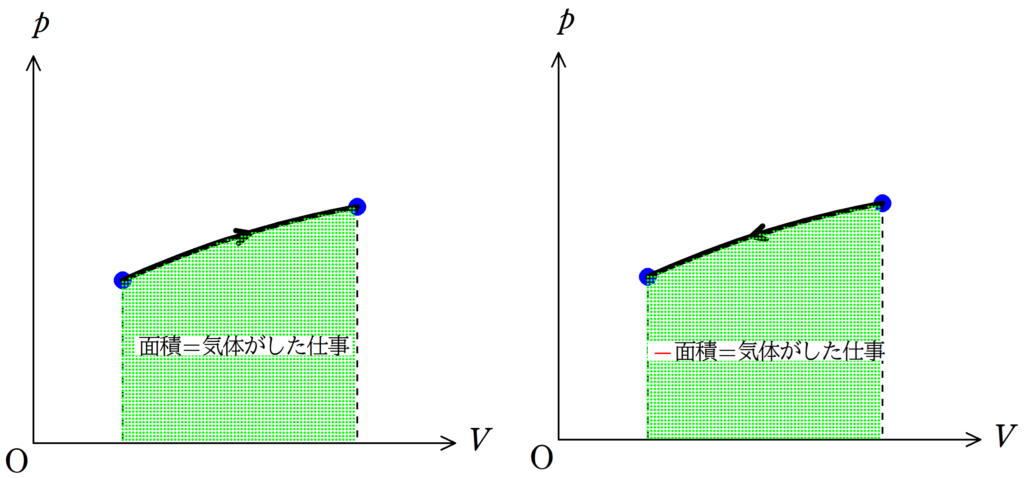
気体がした仕事は上図のように緑色部分の面積を求めることで計算ができる.
ただし,状態変化の矢印が右向きのときは
面積=気体がした仕事
であるが,状態変化の矢印が左向きのときは
-面積=気体がした仕事
である.

それでは,問題を解いてみましょう.

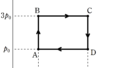
単原子分子理想気体の圧力$p$と体積$V$を縦軸が気体の圧力$p$,横軸が気体の体積$V$のグラフにすると,上図のようになった.
状態Aでは,圧力が$p_{0}$,体積が$V_{0}$,絶対温度が$T_{0}$であった.
まず,状態Aから体積を一定に保ったまま,圧力を$4p_{0}$にした.(状態B)
次に,温度を一定に保ちながら,圧力を$p_{0}$にした.(状態C)
最後に,状態Cから圧力を一定に保ちながら状態Aに戻した.
以下の設問では$p_{0}$,$V_{0}$,$T_{0}$から適当なものを用いて解答せよ.
(1) 状態Bと状態Cの絶対温度$T_{\rm B}$,$T_{\rm C}$をそれぞれ求めよ.
(2) 状態Cにおける気体の体積$V_{\rm C}$を求めよ.
(3) 状態Aから状態Bまでに,気体がした仕事$W_{\rm AB}$,気体の熱量$Q_{\rm AB}$,内部エネルギーの変化$\Delta U_{\rm AB}$をそれぞれ求めよ.
(4) 状態Bから状態Cまでに,気体がした仕事は$W_{\rm BC}=W$であった.気体の熱量$Q_{\rm BC}$,内部エネルギーの変化$\Delta U_{\rm BC}$をそれぞれ求めよ.ただし,この設問においては,$p_{0}$,$V_{0}$,$T_{0}$以外に$W$も用いてよい.
(5) 状態Cから状態Aまでに,気体がした仕事$W_{\rm CA}$,気体の熱量$Q_{\rm CA}$,内部エネルギーの変化$\Delta U_{\rm CA}$をそれぞれ求めよ.
<解答>
(1)

今回も,ボイル・シャルルの法則は使わずに面積の利用をしましょう.


状態Aのときの緑色部分の面積は$p_{0}V_{0}$でした.


そして,状態Bでの面積は$4p_{0}V_{0}$です.
面積が4倍になっているので,絶対温度も4倍になりますね.
また,BからCは問題文に書かれているように,等温変化をしているので,Cの温度もBと同じです.
答:$T_{\rm B}=T_{\rm C}=4T_{0}$
(2)

また,Cの温度も$4T_{0}$ということは,面積も$4p_{0}V_{0}$になるはずです.
すると,次のような式ができます.
$p_{0}V_{\rm C}=4p_{0}V_{0}$ $\therefore$ $V_{\rm C}=4V_{0}$ (答)
(3)

ここから,仕事と熱量と内部エネルギーの変化の計算です.
仕事→$pV$図と$V$軸で囲まれた面積
内部エネルギーの変化→$\Delta U=\dfrac{3}{2}(p^{\prime}V^{\prime}-pV)$
熱量→熱力学第一法則
で計算していきましょう.
問題文に単原子分子理想気体とかいてあるときは,次のことを使うことができる.
定積モル比熱が$\dfrac{3}{2}R$である.すなわち
内部エネルギー$U$は
$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$
内部エネルギーの変化$\Delta U$は
$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$
※$n$:物質量,$T$:絶対温度,$p$:圧力,$V$:体積
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$

気体がした仕事は面積が0なので
$W_{\rm AB}=0$(答)
内部エネルギーの変化の式より
$\Delta U_{\rm AB}=\dfrac{3}{2}(4p_{0}V_{0}-p_{0}V_{0})=\dfrac{9}{2}p_{0}V_{0}$(答)
熱力学第一法則より
$Q_{\rm AB}=\Delta U_{\rm AB}+W_{\rm AB}=\dfrac{9}{2}p_{0}V_{0}$(答)
(4)

温度が変化しないので,
$\Delta U_{\rm BC}=0$ (答)
熱力学第一法則より
$Q_{\rm BC}=\Delta U_{\rm BC}+W_{\rm BC}=W$(答)
(5)

気体がした仕事は,上図の緑色部分の面積を利用する.仕事=-面積であることに注意して
$W_{\rm CA}=-3p_{0}V_{0}$ (答)
内部エネルギーの変化の式より
$\Delta U_{\rm CA}=\dfrac{3}{2}(p_{0}V_{0}-4p_{0}V_{0})=-\dfrac{9}{2}p_{0}V_{0}$ (答)
熱力学第一法則より
$\eqalign{Q_{\rm CA}&=\Delta U_{\ CA}+W_{\rm CA}\\&=-\dfrac{9}{2}p_{0}V_{0}-3p_{0}V_{0}\\&=-\dfrac{15}{2}p_{0}V_{0}}$ (答)



コメント
[…] $pV$グラフの読み取り演習2NEKO引き続き,$pV$グラフを読み取る演習しましょ… […]
すいません、(5)のWca の答え-3PoVoじゃないですか?
ご指摘ありがとうございます.
訂正いたしました.
メガラさん。
その通りです!
ありがとうございます。
後で直します。。