
今回から再び単振動の問題を扱います.その中でもよく出てくる板と物体の運動です.板と物体が接触している状態で単振動をし,ある場所で物体が離れて板のみで単振動をします.
しかし,基本の考え方は同じです.
- 運動方程式を立てる.
- 中心の位置,角振動数,周期を求める.
- 位置$x$を求める.
- 速度,加速度を求める.
今回から”4.速度,加速度を求める”を追加します.さらには,エネルギー保存による解法もありますが,これは後々扱います.それでは問題をみてみましょう.
前回の内容です.
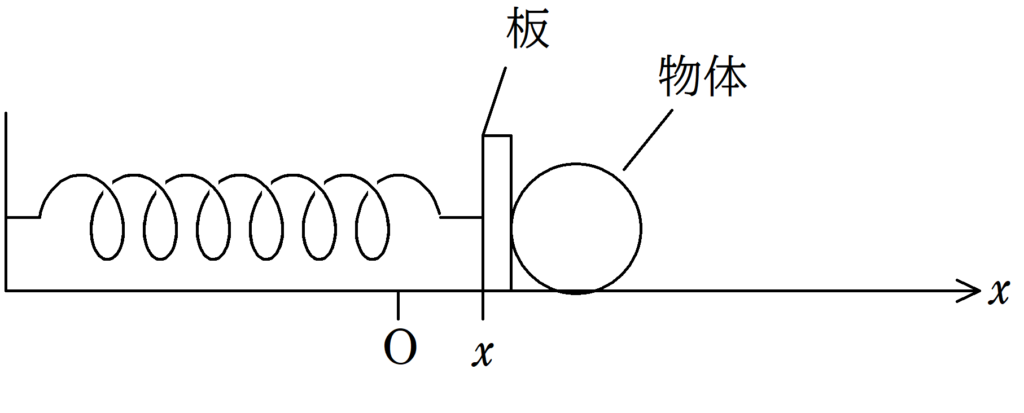
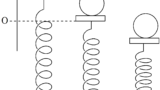
上図のように,ばね定数$k$の軽いばねの一端が壁に固定され,他端は質量$M$の板に固定されている.ばねが自然長になる位置を原点として,ばねが伸びる方向に$x$軸をとる.板のとなりに質量$m$の物体をおき,外力を加えてばねを自然長から$l$だけ縮ませて静かに手をはなしたところ,板と物体はしばらく周期$T_{1}$の単振動をし,ある時刻で板と物体は離れた.その後,物体は等速直線運動をし,板は周期$T_{2}$の単振動をした.以下,板の大きさは無視をし,板と水平面および,物体と水平面との摩擦は無視をしてよい.次の問いに答えよ.
(1) 板と物体が接触している間について,加速度を$x$軸の正の向きに$a$,板と物体の間にはたらく垂直抗力の大きさを$N$とする.板の左端の位置が$x$のとき,板と物体それぞれの運動方程式を立てよ.
(2) (1)のとき,単振動の中心$x_{0}$,角振動数$\omega_{1}$,周期$T_{1}$を$k$,$M$,$m$を用いて表せ.
(3) 板と物体がはなれるときの板の左端の位置$x_{1}$を求めよ.
(4) 板と物体が運動をはじめた時刻を$t=0$とする.板と物体が接触している間の板の左端の位置$x$を$t$,$l$,$M$,$m$,$k$を用いて表せ.
(5) (4)のとき,板と物体がはなれた時刻$t_{1}$を$k$,$M$,$m$を用いて表せ.
(6) (4)のとき,板と物体が接触しているときの板と物体の速度$v$と加速度$a$を$t$,$l$,$M$,$m$,$k$を用いて表せ.
(7) (6)より,板と物体がはなれたときの板と物体の速度$V$を,$l$,$M$,$m$,$k$を用いて表せ.
(8) 板から物体がはなれた後の板の単振動の振幅$A^{\prime}$を$l$,$M$,$m$,$k$を用いて表せ.
<解答>
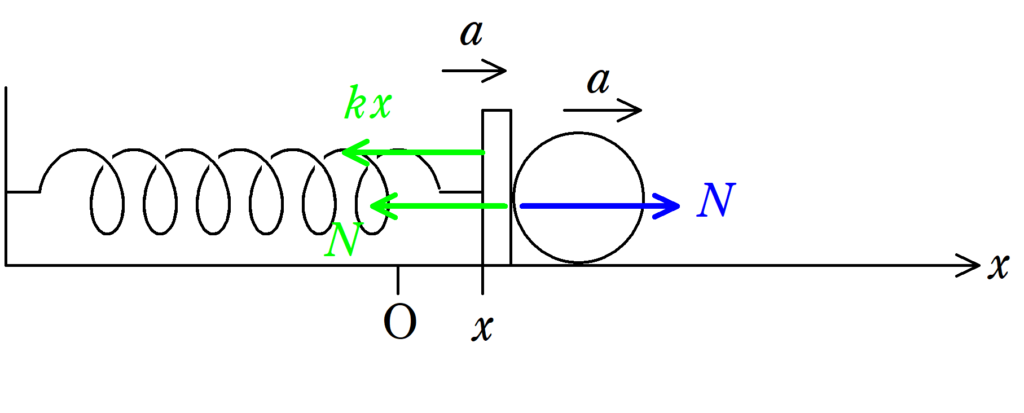
(1) 板の左端の位置が$x$のときに板にはたらく力は$x>0$であれば,弾性力$kx$が$x$軸の負の向き,垂直抗力$N$が負の向きとなります.また,物体にはたらく力は垂直抗力$N$が$x$軸の正の向きにはたらきます.さらに,ここに物体に弾性力$kx$がはたらく...なんて考えるは×です.
板と物体,それぞれの運動方程式は
板:$Ma=-kx-N$ $\dots (\ast)$
物体:$ma=N$ $\dots (2\ast)$
となります.
(2) ($\ast$)と($2\ast$)を足すと
$(M+m)a=-kx$
$\therefore$ $a=-\dfrac{k}{M+m}x$ $\dots (3\ast)$
となるので,単振動することがわかりますね.この運動方程式より
振動の中心$x_{0}=0$,角振動数$\omega_{1}=\sqrt{\dfrac{k}{M+m}}$,周期$T_{1}=2\pi \sqrt{\dfrac{M+m}{k}}$となります.
(3) $(3\ast)$を$(2\ast)$に代入して,
$\eqalign{N&=ma\\&=m\cdot (-\dfrac{k}{M+m}x)\\&=-\dfrac{mk}{M+m}x}$
この式によると,$x=-l$のとき$N=\dfrac{mk}{M+m}l$であり,$x$軸の正の向きに進むと$N$の大きさはだんだんと小さくなり,$x=0$でついには$N=0$となってしまいます.次のことはよく使うので覚えておくとよいでしょう.
板と物体がはなれる→板と物体の間の垂直抗力が0
つまり,板と物体がはなれるのは$x_{1}=0$となります.(自然長で離れます)
(4) (2)より,中心が$x_{0}=0$です.またスタートが$x=-l$なので$-\cos$型です.中心と端っことの距離が$l$なので,振幅は$A=l$です.以上より
$x=x_{0}-A\cos \omega_{1}t=$$-l\cos \sqrt{\dfrac{k}{M+m}}t$ $\dots (4\ast)$
(5) これはわざわざ計算しなくても感覚でいけるかもしれませんが,計算してみます.$(4\ast)$に離れる位置$x=0$を代入すると
$\eqalign{0&=-l\cos \sqrt{\dfrac{k}{M+m}}t\cr\cos\sqrt{\dfrac{k}{M+m}}t&=0\cr \sqrt{\dfrac{k}{M+m}}t&=\dfrac{\pi}{2}, \dfrac{3\pi}{2},\dots}$
この中で一番小さい$t$を選んで,
$\eqalign{\sqrt{\dfrac{k}{M+m}}t&=\dfrac{\pi}{2}\cr t&=\dfrac{\pi}{2}\sqrt{\dfrac{M+m}{k}}}$
これは周期の$\dfrac{1}{4}$に相当します.したがって,答えは$t_{1}=\dfrac{\pi}{2}\sqrt{\dfrac{M+m}{k}}$
(6) $(4\ast)$を時刻$t$で微分すれば速度$v$が導出でき,さらに速度$v$を時刻$t$で微分すれば,加速度$a$が導出できます.まず速度は
$\eqalign{v&=\dfrac{dx}{dt} \\ &=l\sqrt{\dfrac{k}{M+m}}\sin\sqrt{\dfrac{k}{M+m}}t}$ $\dot (5\ast)$
次に加速度は
$\eqalign{a&=\dfrac{dv}{dt}\\&=\dfrac{kl}{M+m}\cos \sqrt{\dfrac{k}{M+m}}t}$
(7) (5)で得た$t_{1}=\dfrac{\pi}{2}\sqrt{\dfrac{M+m}{k}}$を$(5\ast)$に代入しましょう.
$\eqalign{v&=l\sqrt{\dfrac{k}{M+m}}\sin \sqrt{\dfrac{k}{M+m}}\cdot \dfrac{\pi}{2}\sqrt{\dfrac{M+m}{k}}\\&=l\sqrt{\dfrac{k}{M+m}}\sin\dfrac{\pi}{2}\\&=l\sqrt{\dfrac{k}{M+m}}}$
したがって,$V=l\sqrt{\dfrac{k}{M+m}}$
(8) 物体が離れた後の板の加速度を$a^{\prime}$として運動方程式を立てます.板にはたらく水平方向の力は弾性力のみなので
$Ma^{\prime}=-kx$
この運動方程式より,中心が$x=0$,角振動数が$\omega_{2}=\sqrt{\dfrac{k}{M}}$,周期が$T_{2}=2\pi \sqrt{\dfrac{M}{k}}$であることが確認できます.そこで,物体が板から離れた瞬間を$t^{\prime}=0$として,時刻をとりなおすと,振幅を$A^{\prime}$として板の位置$x^{\prime}$は
$x^{\prime}=A^{\prime}\sin \omega_{2}t^{\prime}$ $\dots$ $(6\ast)$
となります.$t^{\prime}=0$のときの速度が$l\sqrt{\dfrac{k}{M+m}}$であるということを使いたいので,$(6\ast)$について時刻$t^{\prime}$で微分すると速度$v^{\prime}$を得ることができます.
$v^{\prime}=A^{\prime}\omega_{2}\cos \omega_{2}t^{\prime}$
$t^{\prime}=0$のときの速度が$l\sqrt{\dfrac{k}{M+m}}$なので,これを上式に代入して
$\eqalign{l\sqrt{\dfrac{k}{M+m}}&=A^{\prime}\omega_{2}\cos 0\cr A^{\prime}\sqrt{\dfrac{k}{M}}&=l\sqrt{\dfrac{k}{M+m}}\cr A^{\prime}&=l\sqrt{\dfrac{M}{M+m}}}$
したがって,$A^{\prime}=l\sqrt{\dfrac{M}{M+m}}$
振幅は物体くっついていたときに比べて小さくなります.

以上でおしまいです.板と物体の単振動の問題は次のポイントをおさえましょう.
- どこで板と物体が離れるのか.
- 離れる前と離れた後の単振動はどのように変わるのか.
立式自体も複雑になってきましたが,基本をおさえて問題の1つ1つを確認するとよいでしょう!
次回も板と物体の単振動ですが,今度は鉛直方向の運動について考えます.
次回の内容です.



コメント
[…] […]
[…] […]
[…] [標準]単振動の演習問題③ 板と物体の運動1NEKO今回から再び単振動の問題… […]