
時間$\Delta t$の間に電流が$\Delta I$変化したとき,コイルの両端の電位の変化はどのように表せばいいの??
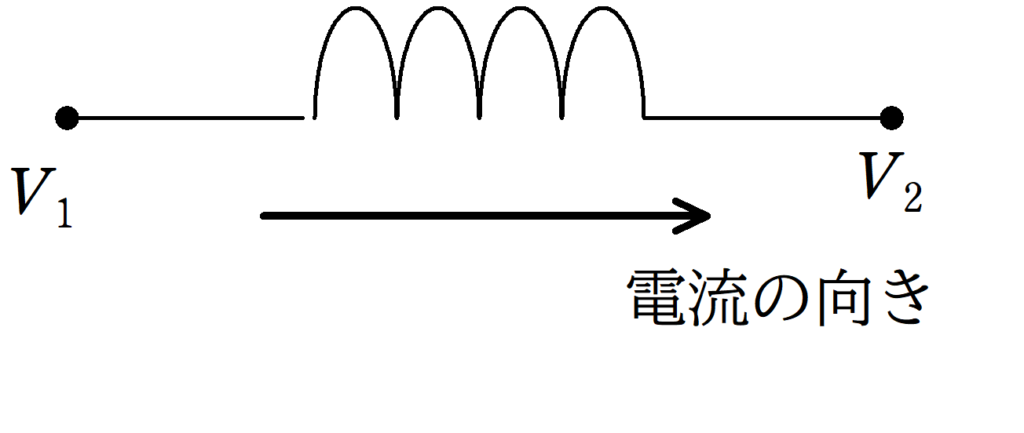

電流の正の向きを上図のように設定すれば,コイルの自己インダクタンスを$L$として,$V_{1}-L\dfrac{\Delta I}{\Delta t}=V_{2}$とすればいいんです.

でも,電流が反対方向に流れていたり,電流がだんだんと小さくなっていくときは起電力の向きが逆になるんだよね?少し面倒そう...

いえ,どんなときでも$V_{1}-L\dfrac{\Delta I}{\Delta t}=V_{2}$で大丈夫です.

え!?でも,誘導起電力の向きって電流の増減によって変化するんだよね?そのことは考えなくてもいいの?

では,順に考えていきましょう.まず,確認することは次のことです.
- 時間$\Delta t$の間に電流が$\Delta I$変化したとする.コイルの自己インダクタンスを$L$とすれば,コイルに生じる自己誘導起電力の大きさ$|V_{L}|$は,$|V_{L}|=L|\dfrac{\Delta I}{\Delta t}|$である.
- 元の電流に戻すような方向に誘導起電力が生じる.

コイルは電流の変化を嫌うんだよね!

はい.その上で次の,[1]電流が正の向きに増加している 場合を考えてみましょう.
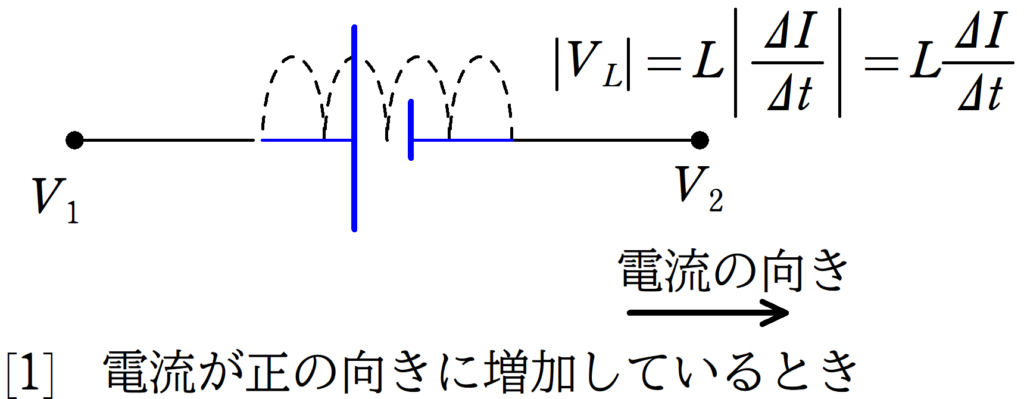

いま,電流がどんどん右方向に増えているから,それをもとにもどそうと左方向に起電力が向いているね!

その通りです.そして,$\Delta I>0$なので,
$|V_{L}|=|L\dfrac{\Delta I}{\Delta t}|=L\dfrac{\Delta I}{\Delta t}$
となります.

だから,$V_{1}-L\dfrac{\Delta I}{\Delta t}=V_{2}$になるんだ!

次に[2]電流が正の向きに減少しているとき を考えてみましょう.
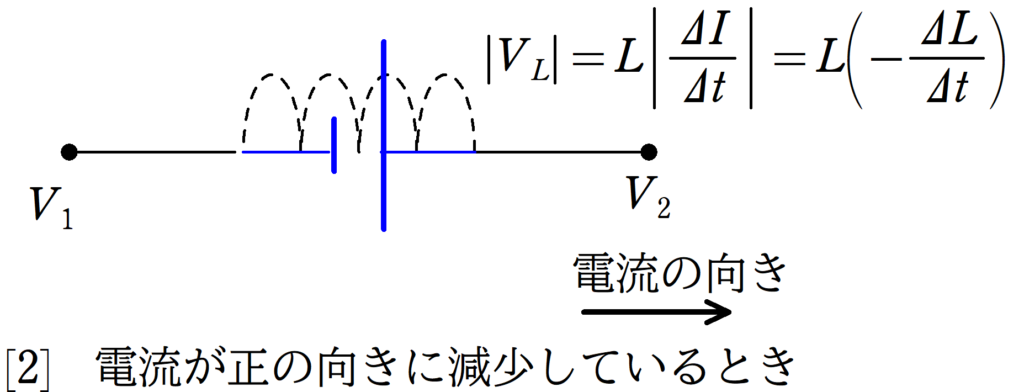

電流がどんどん減っているから右方向に起電力が向いているね.

そうです.電流がたとえば
10A→9A→8A...
と小さくなっていくので,$\Delta I<0$です.だから,誘導起電力の大きさは
$|V_{L}|=L|\dfrac{\Delta I}{\Delta t}|=L\left(-\dfrac{\Delta I}{\Delta t}\right)$
となります.

そうか!だから
$\eqalign{V_{1}+L|\dfrac{\Delta I}{\Delta t}|&=V_{2}\\V_{1}+L\left(-\dfrac{\Delta I}{\Delta t}\right)&=V_{2}\\V_{1}-L\dfrac{\Delta I}{\Delta t}&=V_{2}}$
になるんだ!

そういうことです.結局$V_{1}-L\dfrac{\Delta I}{\Delta t}=V_{2}$となるんです.では次に[3]電流が負の向きに増加しているとき を考えましょう.たとえば
-10A→-11A→-12A...
となっている場合です.これも$\Delta I<0$ですね.
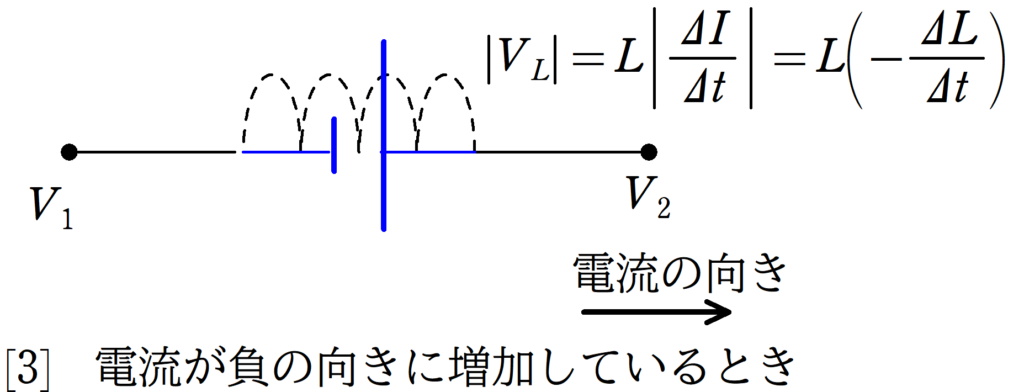

$(-11)-(-10)=-1$だもんね!そして,負の向きに増加しているから,もとにもどすように起電力は右向きだね.すると,
$\eqalign{V_{1}+L|\dfrac{\Delta I}{\Delta t}|&=V_{2}\\V_{1}-L\dfrac{\Delta I}{\Delta t}&=V_{2}}$
だからまた同じ形だ!

最後に電流が負の向きに減少してる場合を考えましょう.たとえば
-10A→-9A→-8A...
となっている場合です.
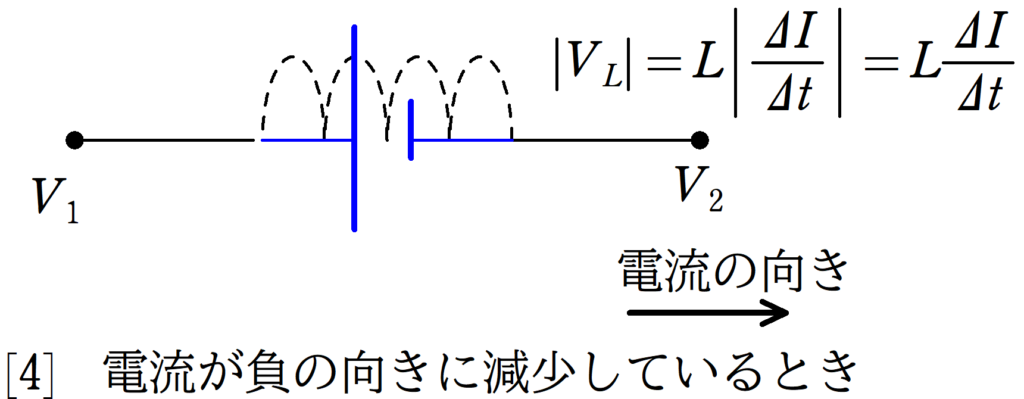

左方向の電流が小さくなっているから,それをもとに戻すように左方向に起電力が生じているね.$(-9)-(-10)=1$だから,$\Delta I>0$か!だから,
$\eqalign{V_{1}-L|\dfrac{\Delta I}{\Delta t}|&=V_{2}\\V_{1}-L\dfrac{\Delta I}{\Delta t}&=V_{2}}$
やっぱり全く同じ形になった!

はい.ということで結論です.

キルヒホッフの法則を立てるとき,電流の向きや増減に関わらず
$V_{1}-L\dfrac{\Delta I}{\Delta t}=V_{2}$
としてよい.


コメント
[…] 回路におけるコイルの扱い […]