
ヤングの実験はやたらと近似が多くて,大変なんだよね..
この機会に整理しておこう.

それでは,まずヤングの実験の概要から話しをします.
ヤングの実験とは
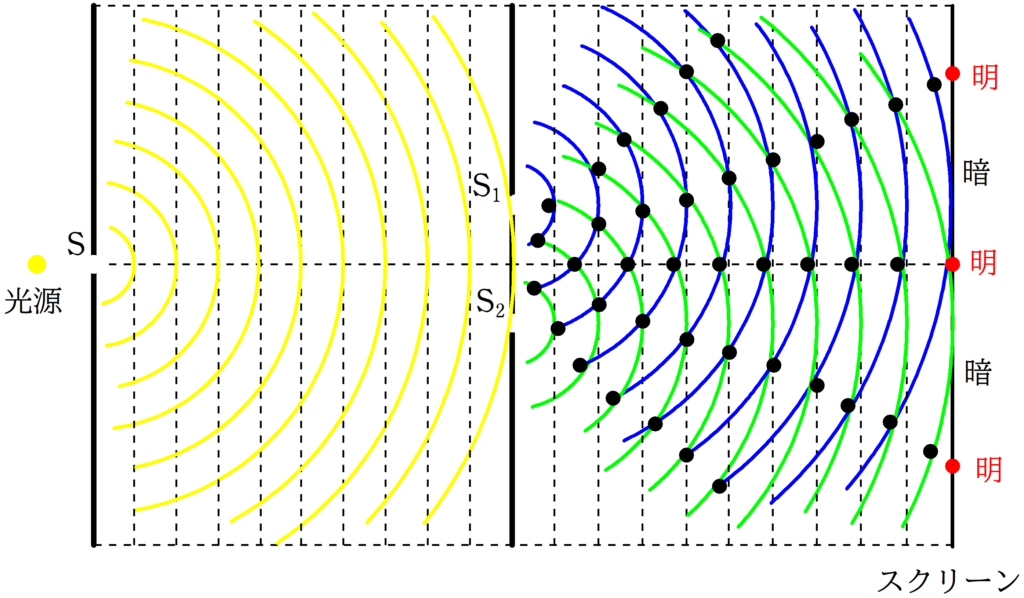

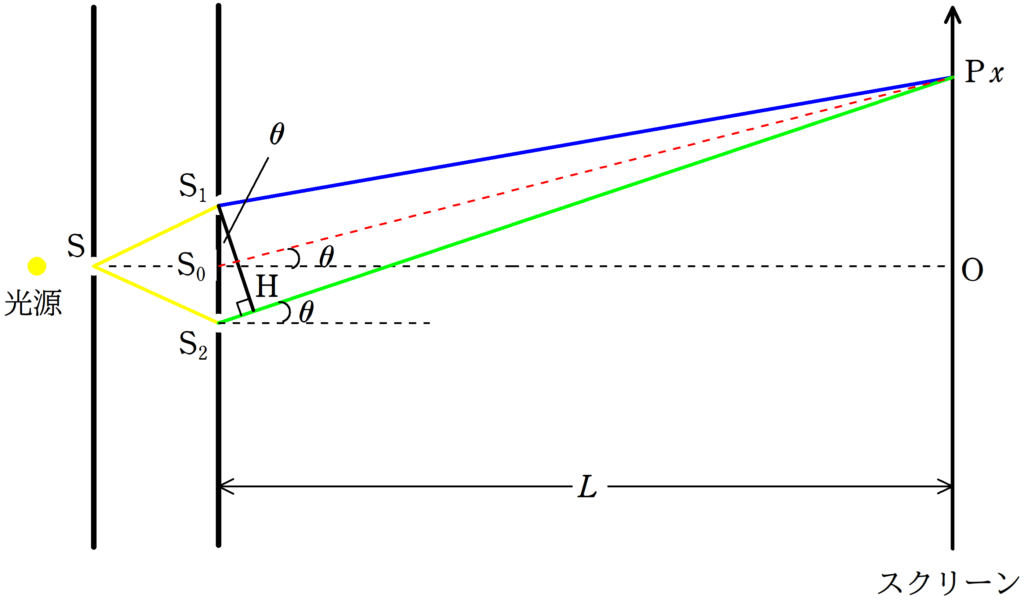
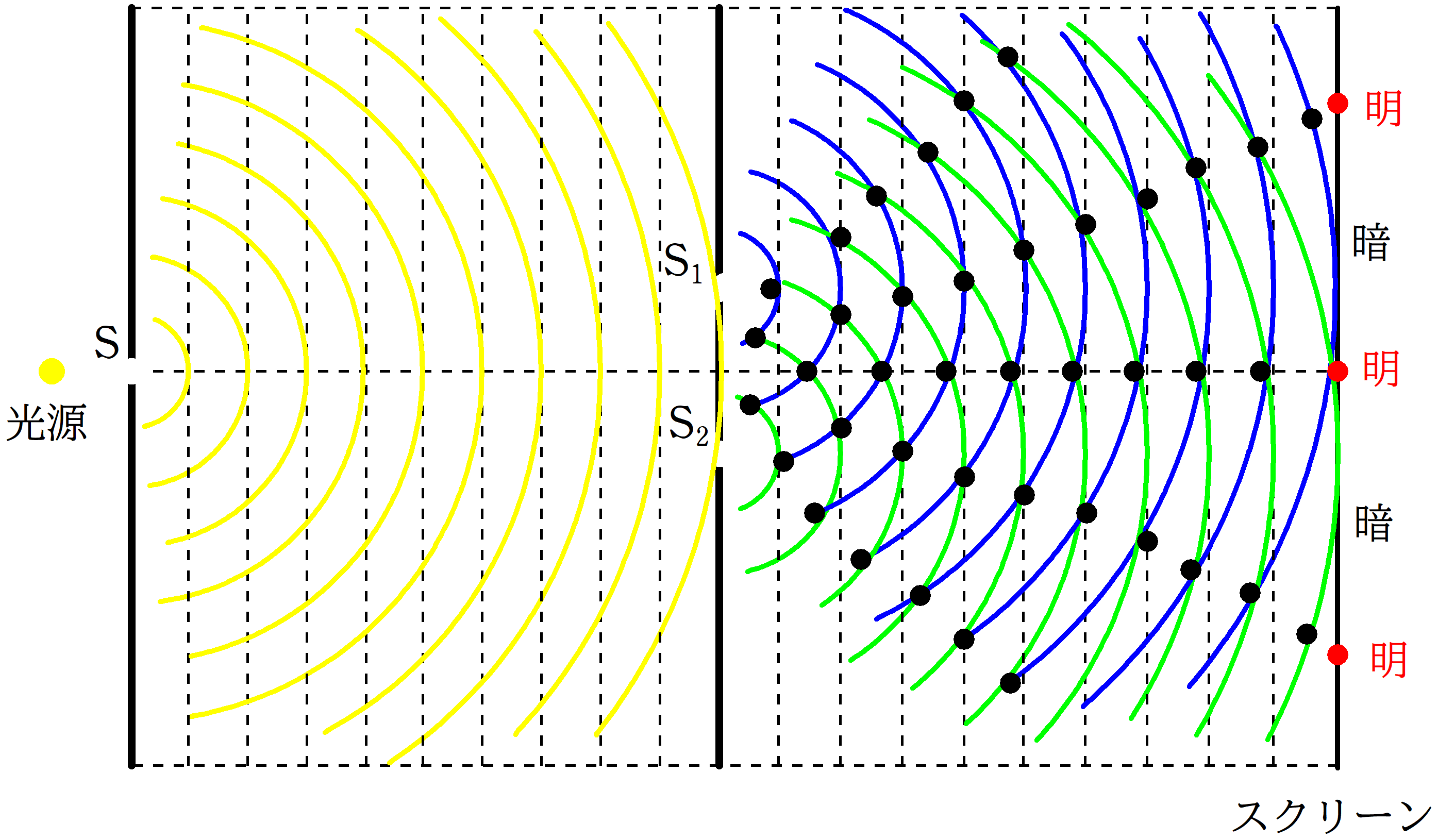
上図のように,単スリットと2スリットとスクリーンを平行において,単スリットに光をあてると,スクリーンに明暗の縞模様ができます.
単スリット$\rm S$から出てきた光が$\rm S_{1}$と$\rm S_{2}$を通りそれぞれから波が回折し,スクリーンで干渉します.

単スリット以外では水面波の干渉と同じだね.
2スリットは位相差をつくる役割があるんだろうけど,単スリットはなんの役割があるの?

単スリットは光源を点光源(大きさが非常に小さい光源)にする役割があります.
簡単に言えば,これをしないと,位相がバラバラのものがスクリーンで重ね合わさるのでうまく縞模様ができなくなります.

実際の実験装置って,2スリットの間の距離はこんなに近くないよね?
あと,2スリットとスクリーンの距離も近すぎている気がする・・・

はい.
誇張して書いてあります.
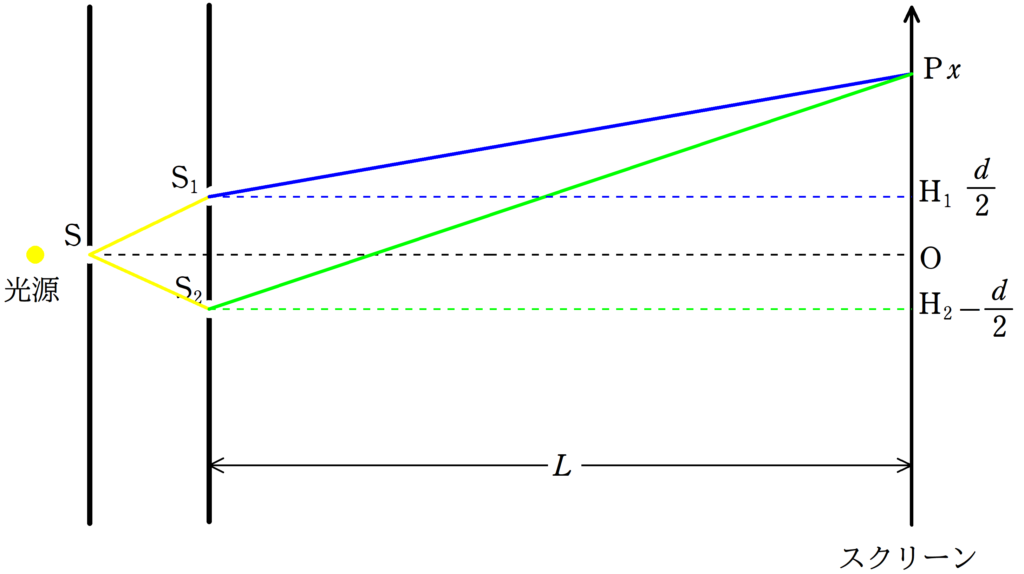
実際は,次のように,スリット間の距離はかなり近いですし,スリットとスクリーンの距離は割と遠いです.
下図を参照してください.(これでも図の限界でちゃんとはかけていません)


青の経路と緑の経路ってほとんど差がないんじゃない??
これで干渉が起こるんだ.

おっしゃる通り,かなり距離の差は小さいです.
そもそも可視光線の波長が$10^{-7}{\rm m}$ほどなので,距離の差もそのくらいです.
ヤングの実験の明暗条件

ヤングの実験における明暗の条件をまとめておきましょう.
$\rm S_{1}$と$\rm S_{2}$の中点からスクリーンにおろした垂線の足を$\rm O$とします.
$\rm O$を原点として,上方向に$x$座標をとります.
スクリーン上の任意の点を$\rm P$とすると,明暗の条件は次のようになります.
以下,$m$を整数とする.
スリットとスクリーンまでの距離を$L$,スリット間の距離を$d$とする.
このとき,${\rm S_{2}P-S_{1}P}=d\cdot \dfrac{x}{L}$である.
★ 明線条件
$\dfrac{\rm S_{2}P-S_{1}P}{\lambda}=m$
★ 暗線条件
$\dfrac{\rm S_{2}P-S_{1}P}{\lambda}=m+\dfrac{1}{2}$

ちなみに,次のことを確認しておきましょう.
波の波長を$\lambda$(波1個分の長さ),波の個数を$N$,波全体の長さを$\Delta L$とすると,次の関係式が成り立つ.
$\Delta L=N\cdot \lambda$
$\therefore N=\dfrac{\Delta L}{\lambda}$

つまり,明暗の条件の左辺は,$\rm S_{2}P-S_{1}P$の中にある波の数を表しているんだね.
明るくなるためには,距離の差がに波整数個分に相当し,暗くなるためには,距離の差が波半整数個分に相当するんだ.

そうですね.
ただ,左辺が正の数とは限らないので,正確には右辺の絶対値が波の数を表しています.
距離の差について

距離の差はどうやって求めるの?

求め方はいくつかあります.
そのうち,オーソドックスな計算と,少し楽な計算の2つを紹介しましょう.
経路差の求め方①

三平方の定理と近似式を使います.
では,まずは三平方の定理です.


求めたいのは${\rm S_{2}P-S_{1}P}$だね.
上図の青色部分の直角三角形と緑色部分の直角三角形について三平方の定理を使って計算してみよう.
青色部分
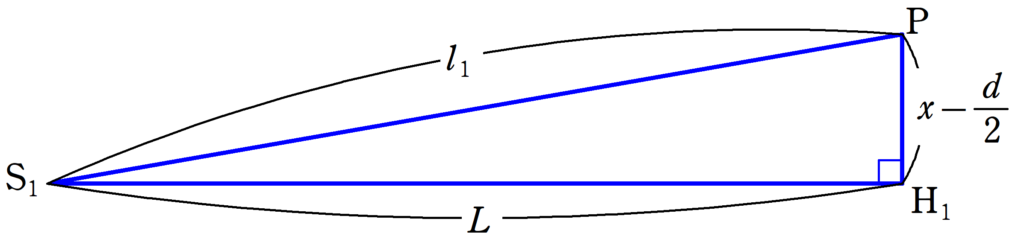
$\eqalign{{\rm S_{1}P}&=\sqrt{L^{2}+(x-\dfrac{d}{2})^{2}}\\&=L\sqrt{1+\displaystyle{\left(\dfrac{x-\frac{d}{2}}{L}\right)}^{2}}}$ $\dots (\ast)$

ここで,$L$は,$d$や$x$比べて十分大きいので,次の近似式を使うことができます.
$|\alpha|\ll1$のとき
$(1+\alpha)^n\fallingdotseq 1+n\alpha$
$(\ast)$の続き
$\eqalign{{\rm S_{1}P}&=L\left\{1+\displaystyle{\left(\dfrac{x-\frac{d}{2}}{L}\right)}^{2}\right\}^{\frac{1}{2}}\\&\approx L\left\{1+\dfrac{1}{2}\displaystyle{\left(\dfrac{x-\frac{d}{2}}{L}\right)}^{2}\right\}\\&=L+\dfrac{x^{2}-dx+\dfrac{d^{2}}{4}}{2L}}$
緑色部分
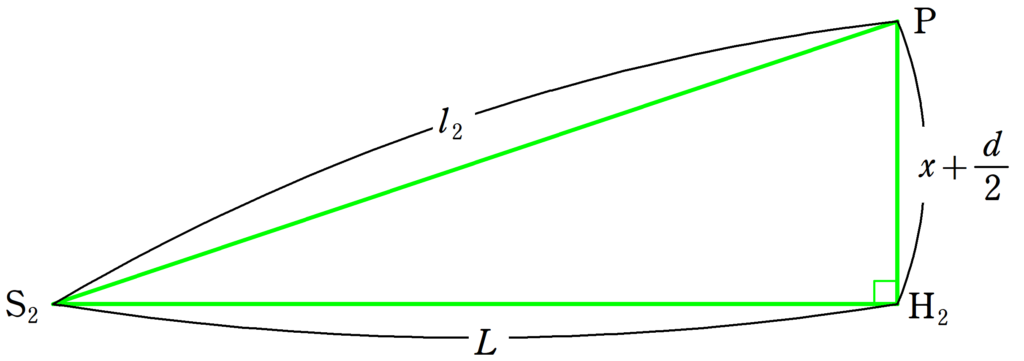
同様の計算,近似をして
$\eqalign{{\rm S_{2}P}&=\sqrt{L^{2}+(x+\dfrac{d}{2})^{2}}\\ &\approx L+\dfrac{x^{2}+dx+\dfrac{d^{2}}{4}}{2L}} $
距離の差を求める
したがって
$\eqalign{{\rm S_{2}P-S_{1}P}&=\left(L+\dfrac{x^{2}+dx+\dfrac{d^{2}}{4}}{2L}\right)-\left(L+\dfrac{x^{2}-dx+\dfrac{d^{2}}{4}}{2L}\right)\\&=d\dfrac{x}{L}}$
経路差の求め方②

次の近似は一見「??」となりますが,計算自体は楽なのでおすすめです.

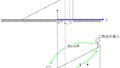
$\rm S_{1}$から$\rm S_{2}P$に垂線を下し,その足を$\rm H$とします.
すると,$\rm S_{1}P$と$\rm HP$がほぼ等しいので$\rm S_{2}H$が経路差になります.
$\angle \rm S_{2}S_{1}H=\theta$とすると,${\rm S_{1}S_{2}}=d$であるから
${\rm S_{2}H}=d\sin\theta$
となります.
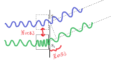
ここで,$|\theta|$が小さいときに使える近似式
$\sin\theta \approx \tan\theta$
より
${\rm S_{2}H}=d\sin\theta\approx d\tan \theta$ $\dots \clubsuit$
となります.
一方,$\rm S_{1}$と$\rm S_{2}$の中点を$\rm S_{0}$とすると,$\rm S_{0}P$と$ \rm S_{2}P$が平行とみなせるので,$\angle \rm OS_{0}P=\theta$とします.
すると,$\triangle{\rm OS_{0}P}$について
$\tan\theta=\dfrac{x}{L}$
となります.
したがって,$\clubsuit$より
${\rm S_{2}H}=d\sin\theta \approx d\tan\theta \approx d\cdot \dfrac{x}{L}$

経路差はある程度頭に入れたうえで問題演習をした方がよさそうだね.

コメント
[…] […]
[…] [ヤングの実験]明暗の条件 […]