交流演習　抵抗をつなぐ

問題

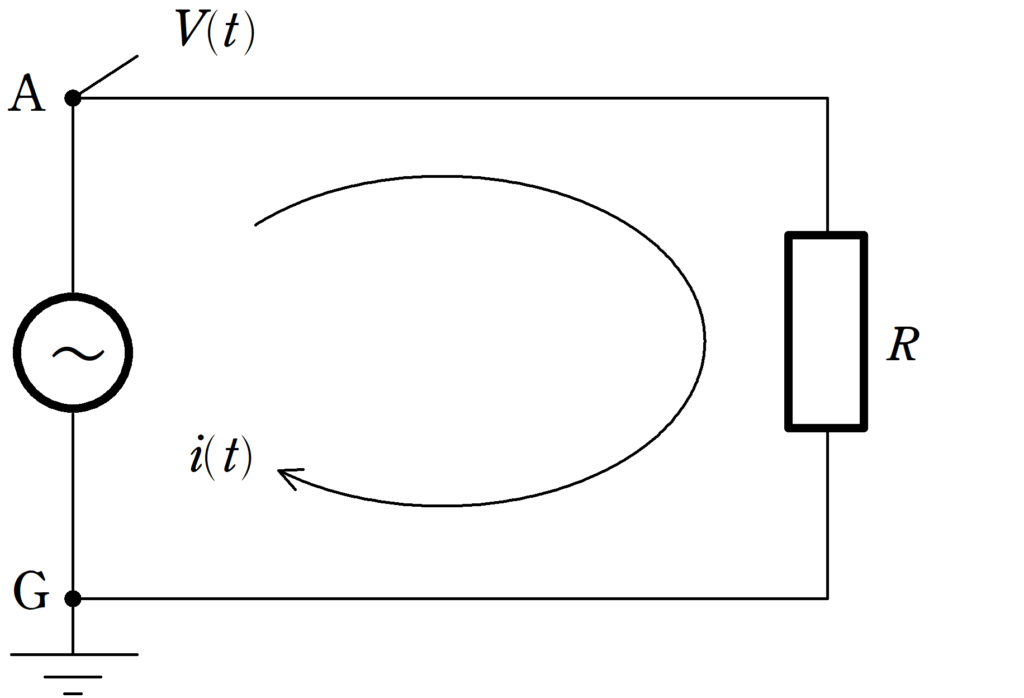
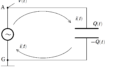
上図のように，交流電源と電気抵抗$R$の抵抗をつないだ．

時刻$t$の交流電源のGに対するAの電位$V(t)$は

$V(t)=V_{0}\sin\omega t$

である．ここで，$V_{0}>0$であり，$\omega$は角周波数である．

このとき，次の問いに答えよ．

(1)　時刻$t$において，回路に流れる電流$i(t)$を$V_{0}$，$R$，$\omega$，$t$を用いて表せ．電流の向きは上図の矢印の向きを正とする．

(2)　時刻$t$において，抵抗で消費する電力$P(t)$を$V_{0}$，$R$，$\omega$，$t$を用いて表せ．

(3)　抵抗で発生する平均消費電力$\bar P$を$V_{0}$と$R$を用いて表せ．

＜解答＞

(1)

PHYさん

オームの法則は瞬間々々成り立ちます．

★　オームの法則

$V(t)=Ri(t)$

$\therefore　i(t)=\dfrac{V(t)}{R}=\dfrac{V_{0}}{R}\sin\omega t$　(答)

(2)　

NEKO

抵抗に電流が流れるたときに消費される電力は次の式を使います．

したがって

$\eqalign{P(t)&=i(t)V(t)\\&=(\dfrac{V_{0}}{R}\sin\omega t) \cdot (V_{0}\sin\omega t)\\&=\dfrac{V_{0}^{2}}{R}\sin^{2}\omega t}$　(答)

(3)

NEKO

平均消費電力は，式変形をすることで求めていきましょう．

NEKO

倍角の式を使って

$P(t)=\dfrac{V_{0}^{2}}{R}\sin^{2}\omega t$

を変形しましょう．

$P(t)=\dfrac{V_{0}^{2}}{R}\cdot \dfrac{1-\cos2\omega t}{2}$

NEKO

$\sin\omega t$と$\cos\omega t$の平均は$0$となります．

なので，$\dfrac{1-\cos2\omega t}{2}$の平均は$\dfrac{1}{2}$となります．

グラフでも確認しておきましょう．

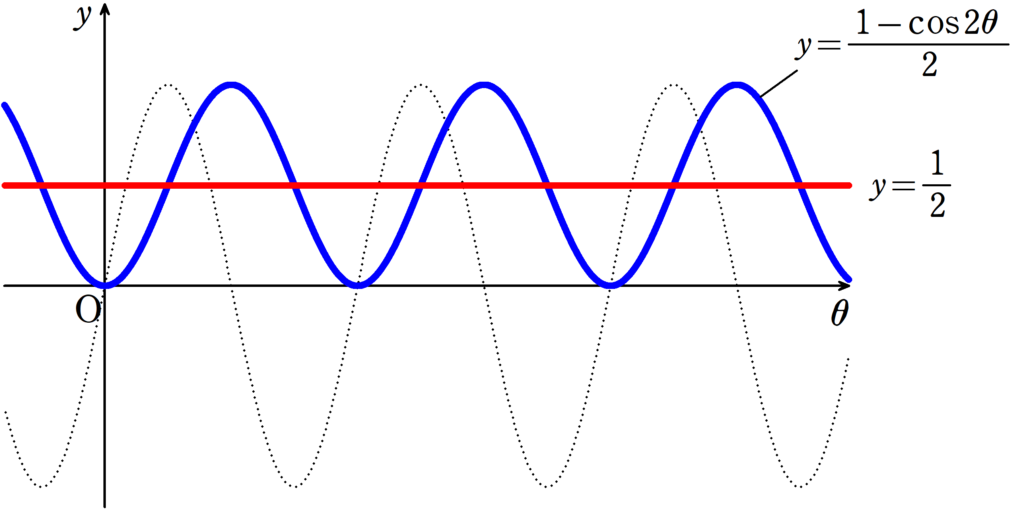
したがって，$\bar P$は

$\bar P=\dfrac{V_{0}^{2}}{2R}$　(答)

なります．