twitterの問題42の解答　円上の$n$個の小球の単振動

東京医科歯科大　単振動の問題 pic.twitter.com/2E8QYSye2d

— フィジクマス (@physicmath2) December 8, 2022

<問題>

<解答>

(1)　問題文に「バネ定数は$k_{0}$/(自然長の長さ)」と書かれているので，まずはこれから求める．

半径$r_{0}$の円周の長さは$2\pi r_{0}$で，ここに$n$個の自然長のバネがあるので1つあたりの自然長のバネの長さは

$\dfrac{2\pi r_{0}}{n}$

である．したがって，バネ定数は

$\dfrac{k_{0}}{\dfrac{2\pi r_{0}}{n}}=\dfrac{nk_{0}}{2\pi r_{0}}$

また，半径が$r_{0}+x$での円周の長さは$2\pi(r_{0}+x)$で，このとき，1つあたりのバネの長さは$\dfrac{2\pi(r_{0}+x)}{n}$である．1つあたりのバネの自然長が$\dfrac{2\pi r_{0}}{n}$なので，1つあたりのバネの伸びは

$\dfrac{2\pi(r_{0}+x)}{n}-\dfrac{2\pi r_{0}}{n}=\dfrac{2\pi x}{n}$

なので，小球が1つのバネから受ける力の大きさは

$\dfrac{\cancel{n}k_{0}}{\bcancel{2\pi} r_{0}}\times \dfrac{\bcancel{2\pi} x}{\cancel{n}} =\dfrac{k_{0}}{r_{0}}x$(答)

(2)　運動方程式を立てて，角振動数を求める．

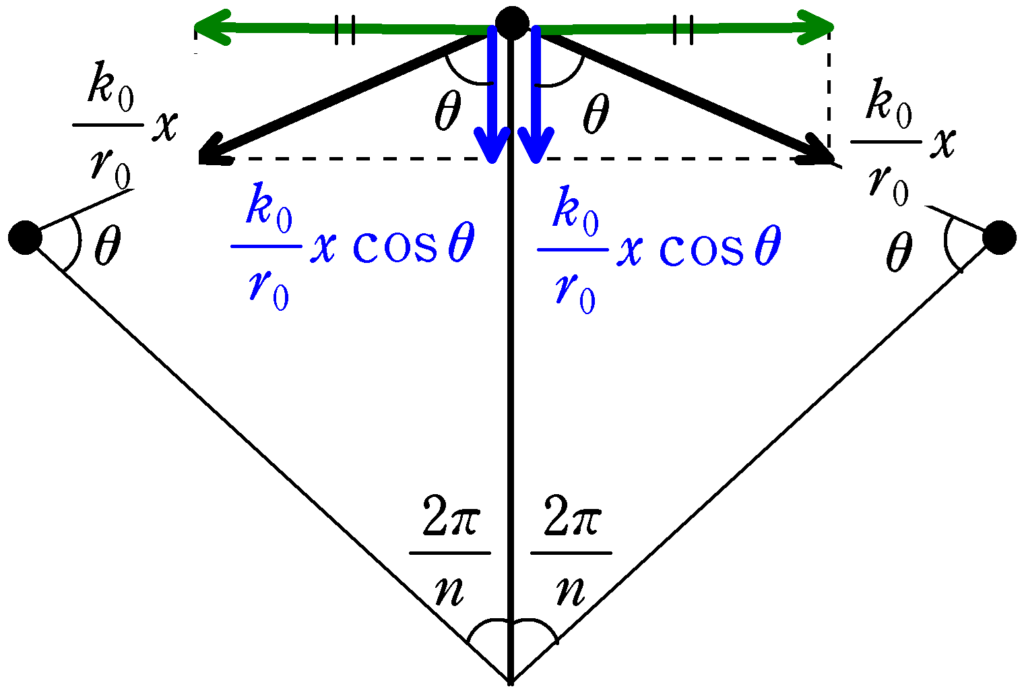
小球と円の中心により，$n$個の2等辺三角形に分割できる．1つの2等辺三角形の頂角は$\dfrac{2\pi}{n}$で，三角形の角度の和は$\pi$だから，底角$\theta$は

$\theta+\theta+\dfrac{2\pi}{n}=\pi$　$\theta=\dfrac{n-2}{2n}\pi$

上図のように，小球が1つのバネに引っ張られる力を中心方向とそれに垂直な方向に分解する．垂直な方向の力は力の大きさが同じで向きが逆なので打ち消す．中心方向の力の和の大きさは

$\dfrac{k_{0}}{r_{0}}x \cos\theta \times 2=\left\{\dfrac{2k_{0}}{r_{0}}\cos\left(\dfrac{n-2}{2n}\pi\right)\right\}x$

であり，$\cos\left(\dfrac{n-2}{2n}\pi\right)=\cos\left(\dfrac{\pi}{2}-\dfrac{\pi}{n}\right)=\sin\left(\dfrac{\pi}{n}\right)$なので，1つ小球について，小球から中心に向かう方向と逆方向を正として加速度を$a$とすると，運動方程式は

$\dfrac{M}{n}a=-\left\{\dfrac{k_{0}}{r_{0}}\sin\left(\dfrac{\pi}{n}\right)\right\}x$

$\therefore\,\, a=-\left\{\dfrac{2nk_{0}}{Mr_{0}}\sin\left(\dfrac{\pi}{n}\right)\right\}x$

したがって，角振動数$\omega$は

$\omega=\sqrt{\dfrac{2nk_{0}}{Mr_{0}}\sin\left(\dfrac{\pi}{n}\right)}$(答)

(3)　

$\displaystyle{\lim_{\theta \to 0}\dfrac{\sin\theta}{\theta}=1}$

を用いる．(2)より角振動数は

$\omega=\sqrt{\dfrac{2\cancel{n}k_{0}}{Mr_{0}}\dfrac{\sin\left(\dfrac{\pi}{n}\right)}{\dfrac{\pi}{n}}\times \dfrac{\pi}{\cancel{n}}}$

$n\to \infty$で$\dfrac{\pi}{n}\to 0$であるから

$\omega\to \sqrt{\dfrac{2\pi k_{0}}{Mr_{0}}}$

周期$T$と角振動数$\omega$の関係より

$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{Mr_{0}}{2\pi k_{0}}}=\sqrt{\dfrac{2\pi Mr_{0}}{k_{0}}}$ (答)