twitterの問題36の解答（電場の重ね合わせ）

<問題>

<解答>

平面に一様に分布した電荷がつくる電場の大きさの話はこちら

平面に分布された電荷がつくる電場は距離によらず一定

PHYさん 十分広い平面に一様に分布された電荷がつくる電場について，次のことを知っておくとよいでしょう． 平面に一様に分布した電荷がつくる電場 十分に広い平面に一様な電荷$Q$が分布している． 真空の誘電率を$\varepsilon_{0}...

physicmath.net

2020.12.17

電場の平面極板がつくる電場の重ね合わせの話はこちら

コンデンサーの極板の電荷分布

PHYさん 平らな極板2枚を平行に固定してコンデンサーをつくりましょう． もともと，極板には電荷が蓄えられていない状況で電池につなぐと，片方の極板からもう片方の極板に電荷が移動し，2枚の極板に電荷が蓄えられます． このとき，2枚の極板の電荷...

physicmath.net

2020.12.21

平面に一様に分布した電荷がつくる電場

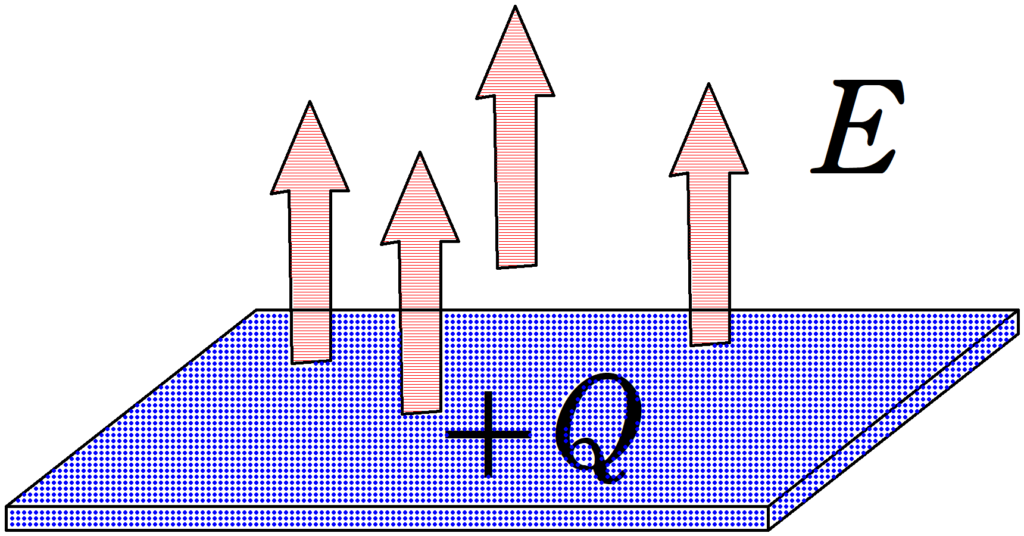
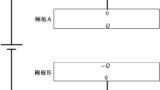
十分に広い平面に一様な電荷$Q$が分布している．

真空の誘電率を$\varepsilon_{0}$，平面の面積を$S$とするとき，電場の大きさ$E$は

$E=\dfrac{|Q|}{2\varepsilon_{0}S}$

これは，電場が距離によらず一定であることを意味している．

下図において，上方向を電場の正方向とする．

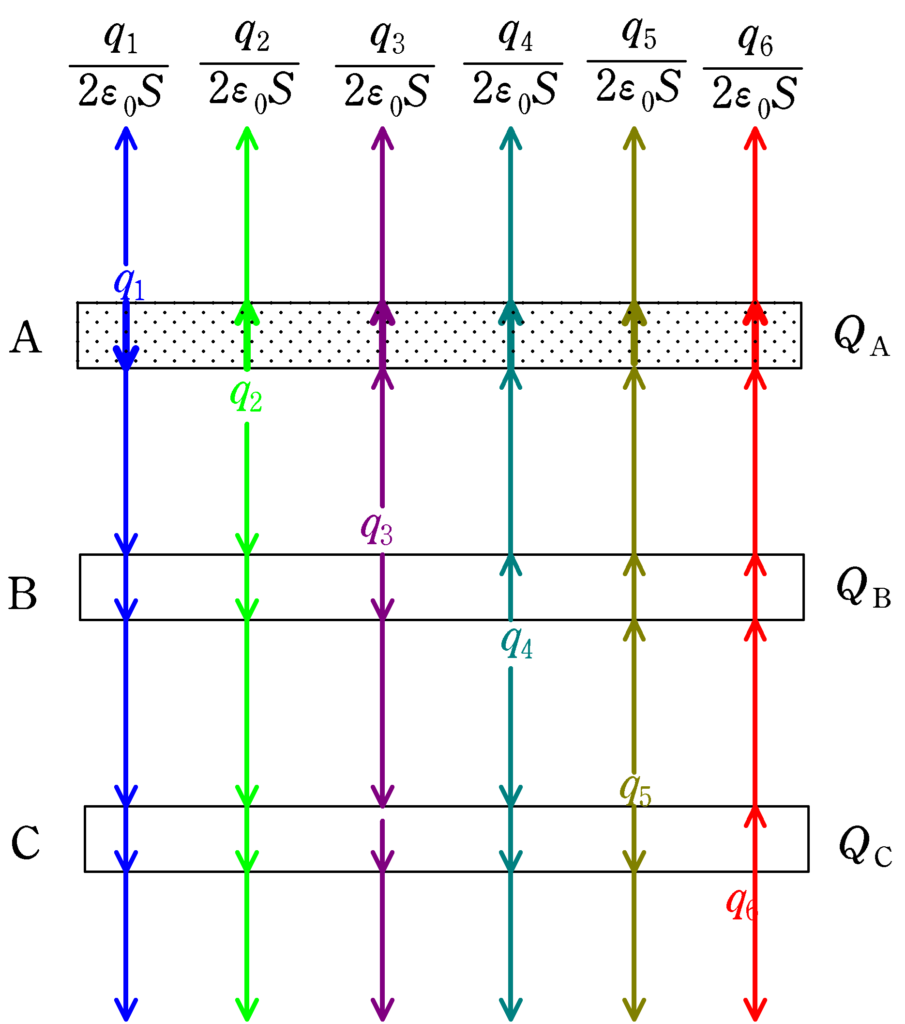
★　極板A内部の電場は$0$より

$\dfrac{1}{2\varepsilon_{0}S}(-q_{1}+q_{2}+q_{3}+q_{4}+q_{5}+q_{6})=0$

$\therefore\,\, -q_{1}+q_{2}+q_{3}+q_{4}+q_{5}+q_{6}=0$

また，$q_{3}+q_{4}=Q_{\rm B}，q_{5}+q_{6}=Q_{\rm C}$を上式に代入して

$-q_{1}+q_{2}+Q_{\rm B}+Q_{\rm C}=0$

$\therefore\,\, q_{1}-q_{2}=Q_{\rm B}+Q_{\rm C}　\cdots (\ast)$

また，

$q_{1}+q_{2}=Q_{\rm A}　\cdots (2\ast)$

$(\ast)，(2\ast)$を解けば

$q_{1}=\dfrac{Q_{\rm A}+Q_{\rm B}+Q_{\rm C}}{2}，q_{2}=\dfrac{Q_{\rm A}-Q_{\rm B}-Q_{\rm C}}{2}$　(答)