
十分広い平面に一様に分布された電荷がつくる電場について,次のことを知っておくとよいでしょう.
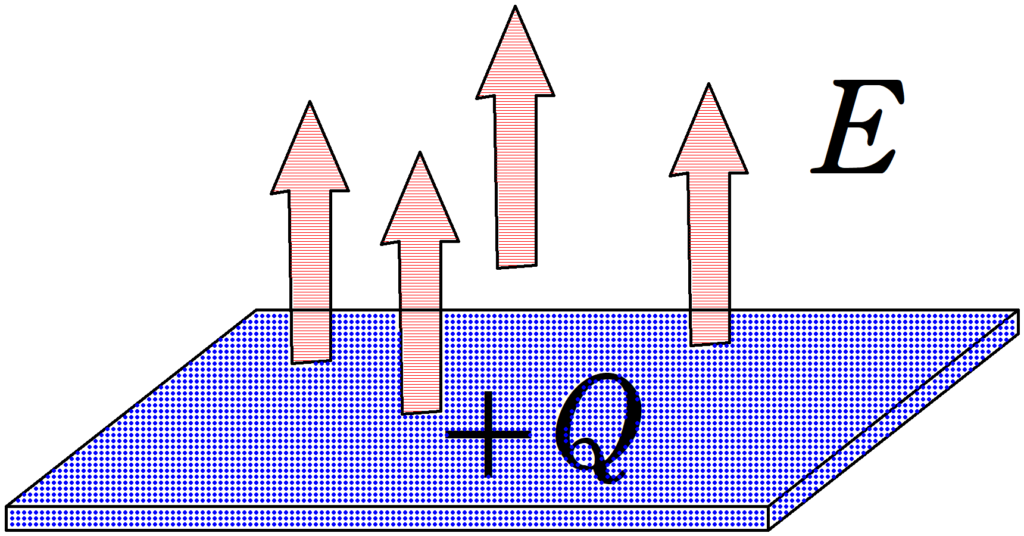
十分に広い平面に一様な電荷$Q$が分布している.
真空の誘電率を$\varepsilon_{0}$,平面の面積を$S$とするとき,電場の大きさ$E$は
$E=\dfrac{|Q|}{2\varepsilon_{0}S}$
これは,電場が距離によらず一定であることを意味している.

上のことを導くには,次の3つのことを知っておく必要があります.
- 電気力線による電場の定義(ガウスの法則)
- 電荷$Q$から出てくる電気力線の本数$N$は$Q$で決まる
- 平面に一様に分布されている電荷は平面に垂直な電場をつくる

それでは,1つ1つ確認していきましょう.
1.電気力線による電場の定義(ガウスの法則)

電荷$Q$が,距離$r$の位置につくる電場の大きさ$E$は,誘電率$\varepsilon_{0}$を用いて次のようになります.
$E=\dfrac{1}{4\pi \varepsilon_{0}}\dfrac{|Q|}{r^2}$
しかし,今回は電場を次のように定義しましょう.
$1\rm m^{2}$あたりを垂直に貫く電気力線の本数を$n$とする.
このとき,電場の大きさ$E$は
$E=n$
つまり,面積$S[\rm m^{2}]$を垂直に貫く電気力線の本数を$N$とすると,$n=\dfrac{N}{S}$であるから
$E=\dfrac{N}{S}$
である.

電場の大きさを電気力線の密度で定義するんだね.
2.電荷$Q$から出てくる電気力線の本数$N$は$Q$で決まる
電荷$Q$から出る(または入る)電気力線の数$N$は,真空におけるクーロンの比例定数を$k_{0}$,真空の誘電率を$\varepsilon_{0}$とすると
$N=4\pi k_{0}|Q|=\dfrac{|Q|}{\varepsilon_{0}}$

これは,次のように確かめることができます.
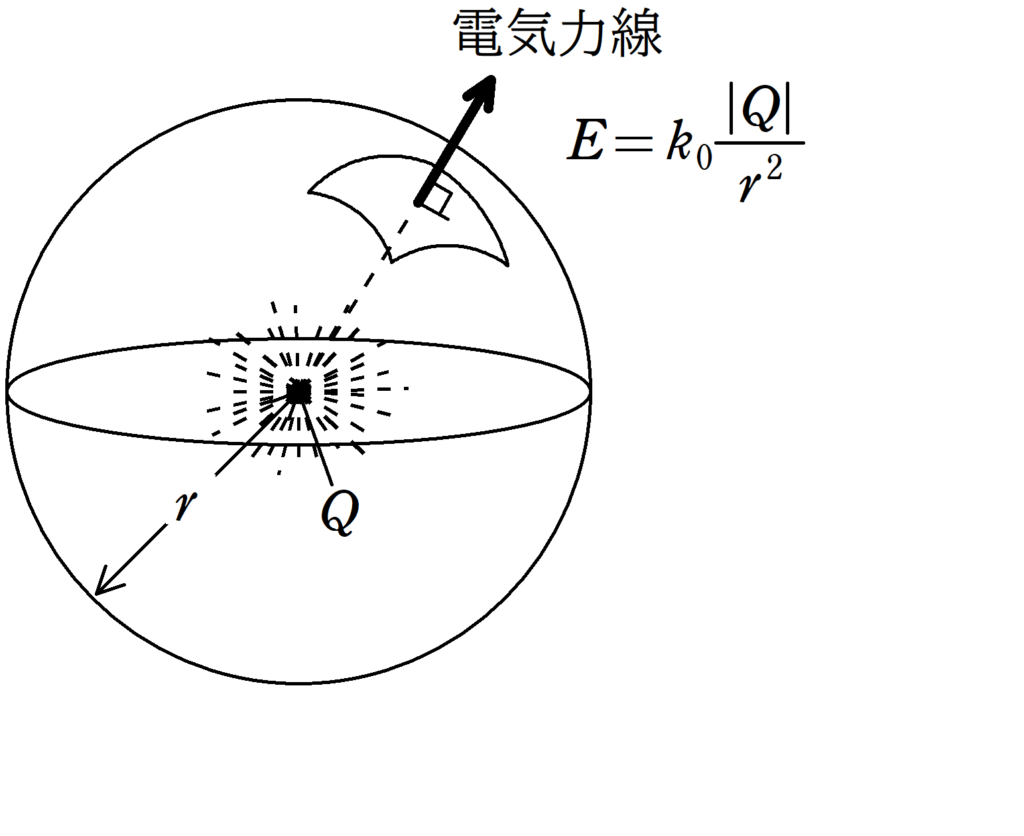

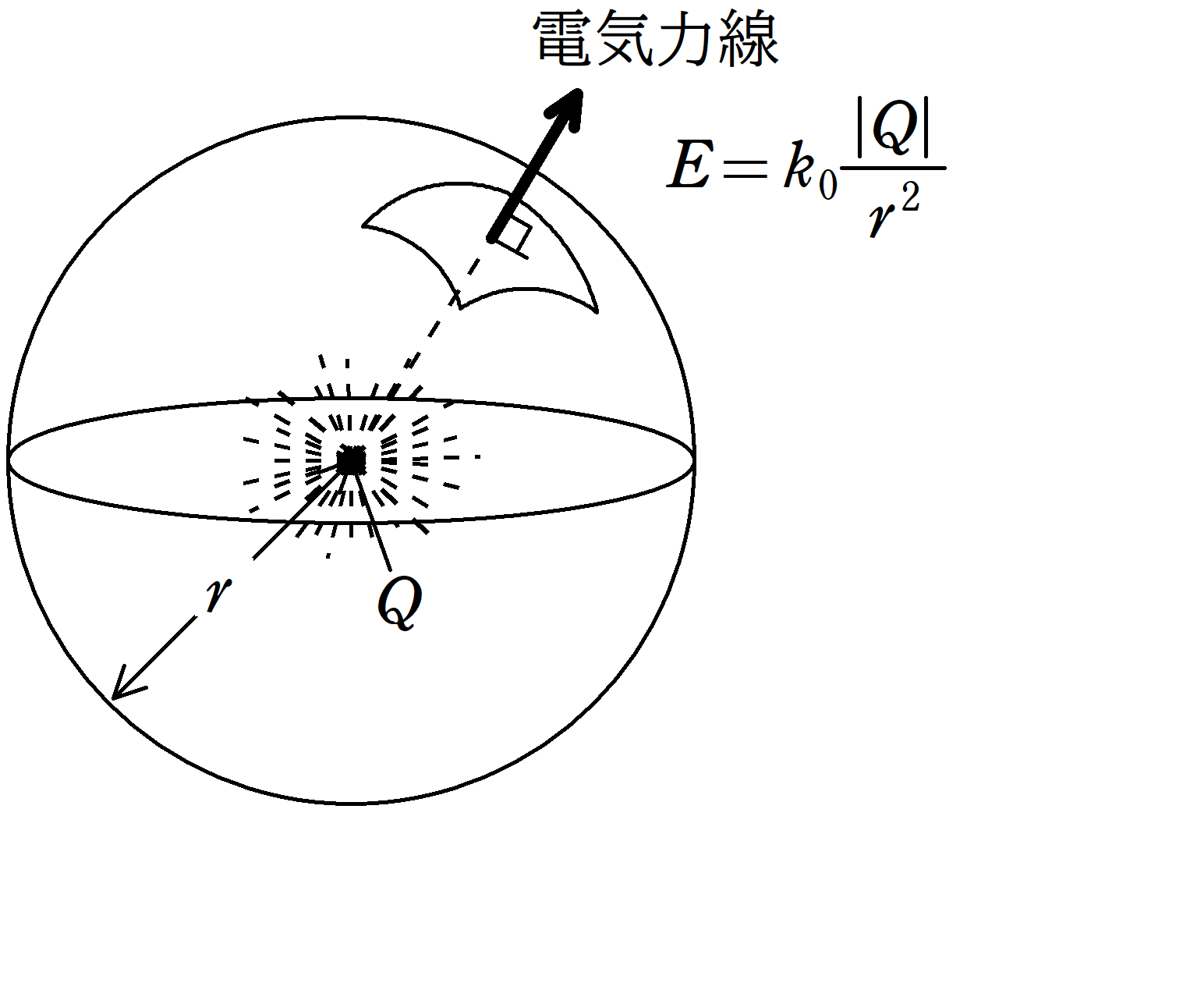
上図のように電荷$Q$の点電荷を考えます.
点電荷が距離$r$の位置につくる電場の大きさ$E$は
$E=k_{0}\dfrac{|Q|}{r^{2}}$ $\dots (\ast)$
です.
電荷がある場所を中心として,半径$r$の球を考えます.
表面積は$S=4\pi r^{2}$ですね.
すると,電気力線による電場の大きさの定義から
$E=\dfrac{N}{S}=\dfrac{N}{4\pi r^{2}}$ $\dots (2\ast)$
$(\ast)$と$(2\ast)$より,$N$を求めます.
$(\ast)$と$(2\ast)$より
$\dfrac{N}{4\pi r^{2}}=k_{0}\dfrac{|Q|}{r^{2}}$
$\therefore N=4\pi k_{0}|Q|=\dfrac{|Q|}{\varepsilon_{0}}$
3.平面に一様に分布されている電荷は平面に垂直な電場をつくる
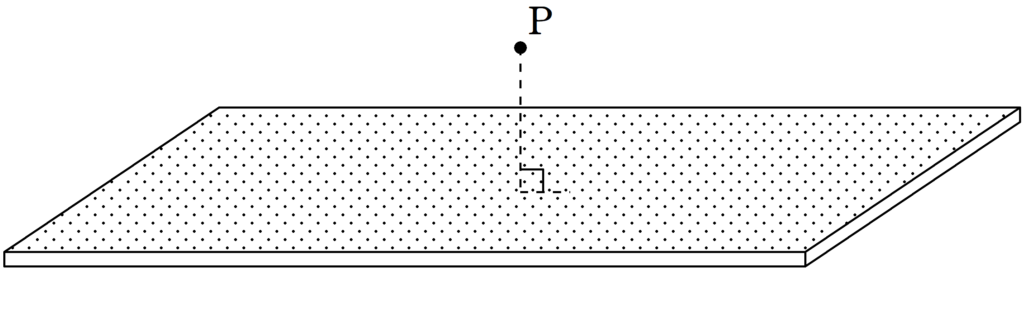

平面から少しはなれた点Pにおける電場の向きを考えてみましょう.
ここで,次の約束をします.
1.平面は十分広い
2.平面の端の電場のゆがみは無視をする
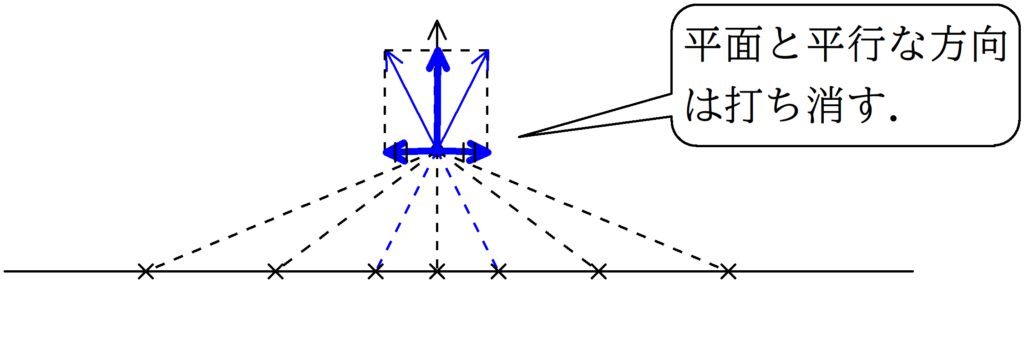

Pの真下にある電荷がつくる電場は真上(平面に対して垂直な方向)に向きます.
しかし,Pの真下からずれた場所にある電荷がつくる電場は上図のように斜めになります.

それじゃあ,電場は平面に垂直になっていないんじゃないの??

しかし,Pに真下にある点を対称とした点電荷がつくる電場によって平面に平行な方向が打ち消されます.
平面は十分広いと考えているので,Pの真下の右方向も左方向も同じ数だけ電荷があると考えているのです.

それで,平面がつくる電場は平面に垂直な向きになるんだね.

それでは,準備ができたので,平面に分布されている電荷がつくる電場の大きさを計算しましょう.
下図は,面積$S$の十分広い平面に電荷$Q$が一様に分布されている図です.
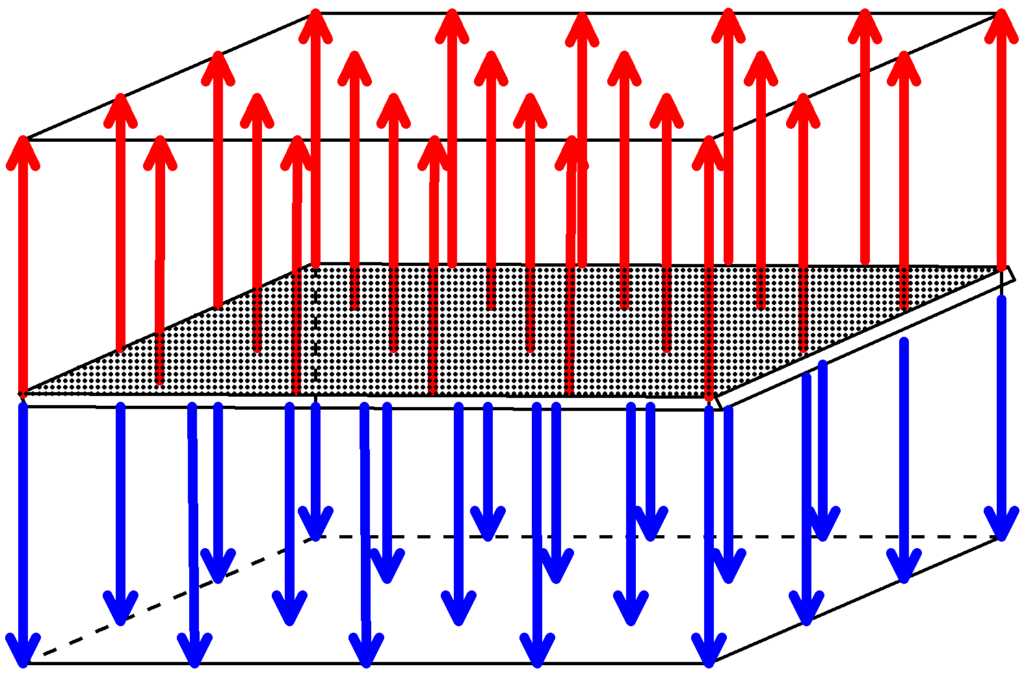

平面に分布された電荷$Q$は上方向(赤色線)と下方向(青色線)の2つに分かれるでしょう.
そして,その数は同じはずです.
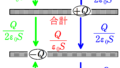
赤色線の数と青色線の数を合わせると$\dfrac{|Q|}{\varepsilon_{0}}$なので,たとえば赤色の電気力線の数$N_{1}$は
$N_{1}=\dfrac{|Q|}{2\varepsilon_{0}}$
となります.
そして,電気力線による電場の定義から平面に上側の電場の大きさ$E_{1}$は
$E_{1}=\dfrac{N_{1}}{S}=\dfrac{|Q|}{2\varepsilon_{0}S}$
となります.

最後にもう一度まとめておきましょう.
十分に広い平面に一様な電荷$Q$が分布している.
真空の誘電率を$\varepsilon_{0}$,平面の面積を$S$とするとき,電場の大きさ$E$は
$E=\dfrac{|Q|}{2\varepsilon_{0}S}$
これは,電場が距離によらず一定であることを意味している.


コメント
[…] […]
[…] […]
[…] […]
[…] 平面に分布する電荷は距離のよらず一定 […]