電荷保存則演習5 コンデンサーと抵抗がある場合

問題

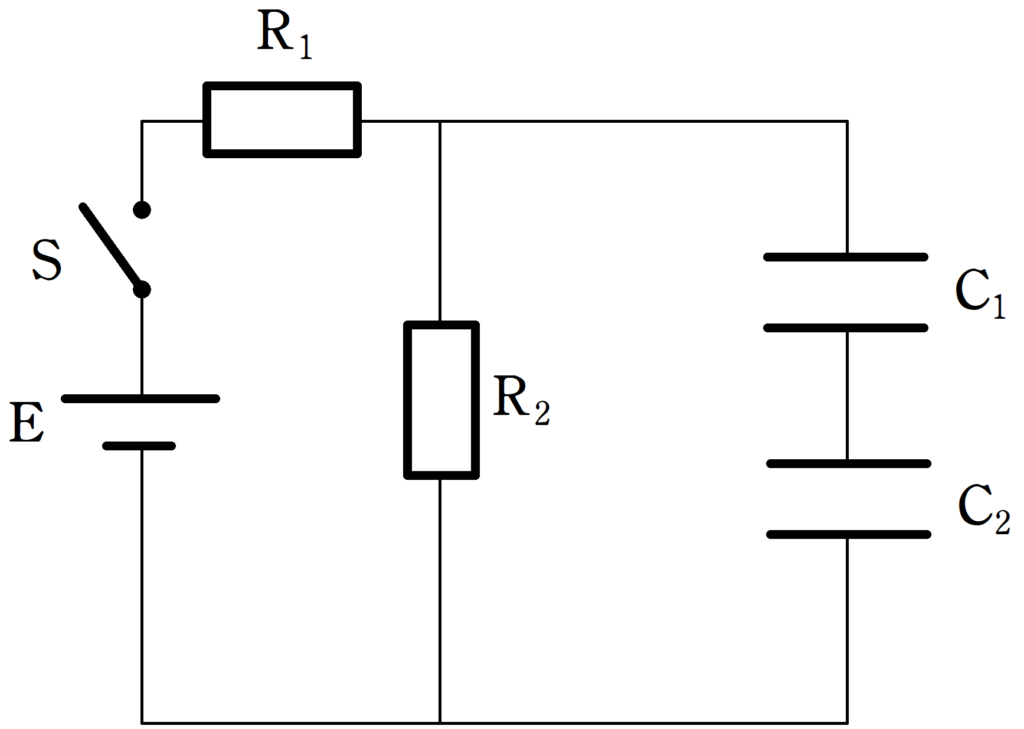
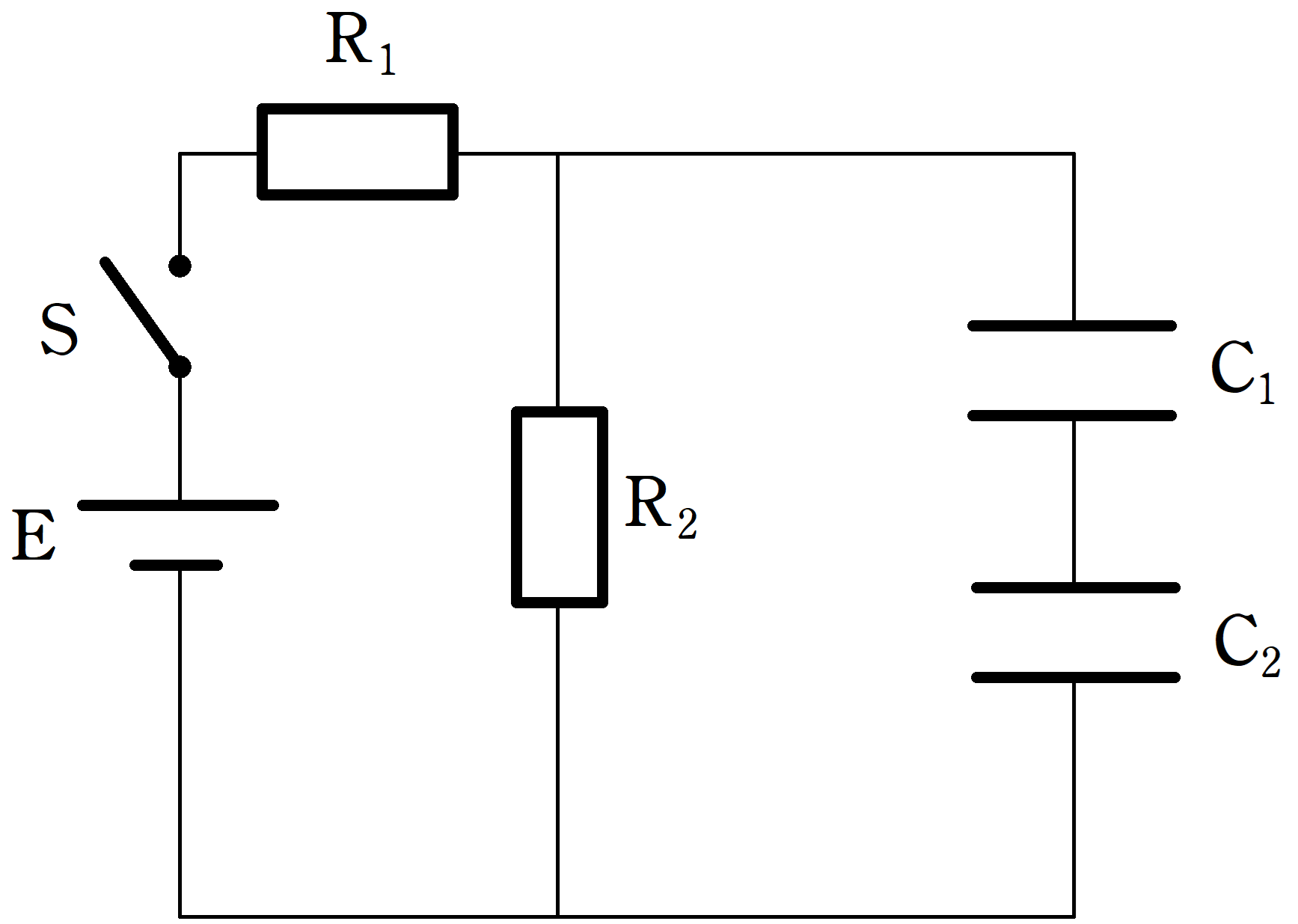
起電力$V$で内部抵抗が無視できる電池$\rm E$，スイッチ$\rm S$，抵抗値$R$，$2R$の電気抵抗$\rm R_{1}$，$\rm R_{2}$，電気容量$C$，$2C$のコンデンサー$\rm C_{1}$，$\rm C_{2}$が上図のように接続されている．

はじめ，$\rm C_{1}$，$\rm C_{2}$には電荷が蓄えられていなく，スイッチが開かれていた．

この状態から，スイッチを閉じて十分時間が経ったときに，$\rm C_{1}$，$\rm C_{2}$に蓄えられている電荷を求めよ．

＜解答＞

NEKO

前回の問題はこちらです．

電荷保存則とコンデンサーの式を用いて解きます．

しかし，この問題では，スイッチを閉じて十分時間が経つと，コンデンサーには電荷が流れませんが，抵抗$\rm R_{1}$，$\rm R_{2}$と電池$\rm E$には電流が流れています．

そこで，キルヒホッフ則も立てます．

電気容量の定義式（コンデンサーの基本式）

コンデンサーに蓄えられている電荷を$Q$，コンデンサー間の電圧を$V$とすれば，コンデンサーの電気容量$C$は

$C=\dfrac{Q}{V}$

実際は

$Q=CV$

として使うことが多い．

電荷保存則

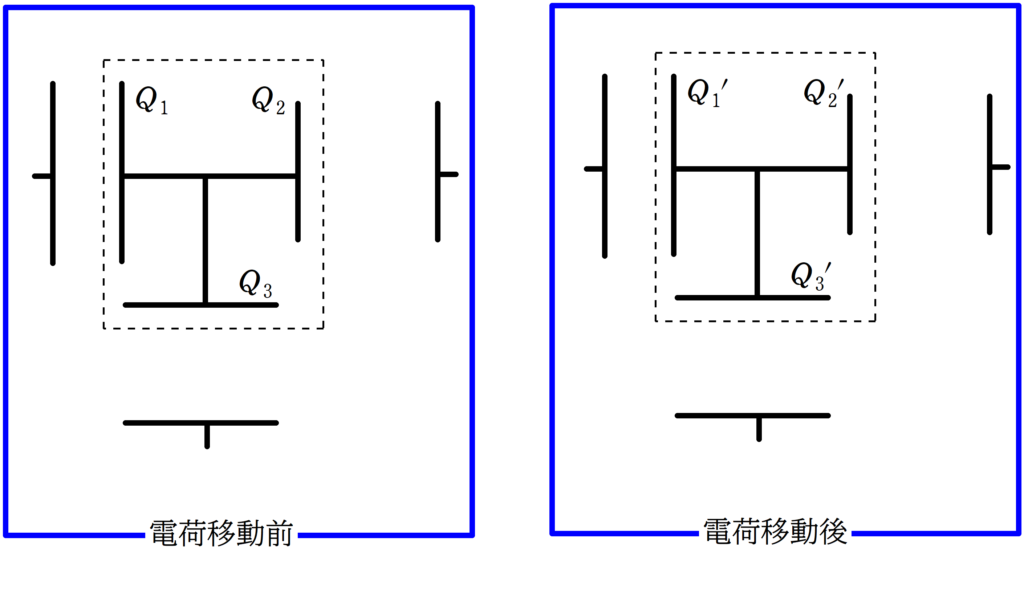
孤立した部分の電荷の総和は変化しない．これを電荷保存則という．

たとえば，上図のように点線部分の孤立した場所の電荷について考えると

$Q_{1}+Q_{2}+Q_{3}=Q_{1}^{\prime}+Q_{2}^{\prime}+Q_{3}^{\prime}$

が成り立つ．

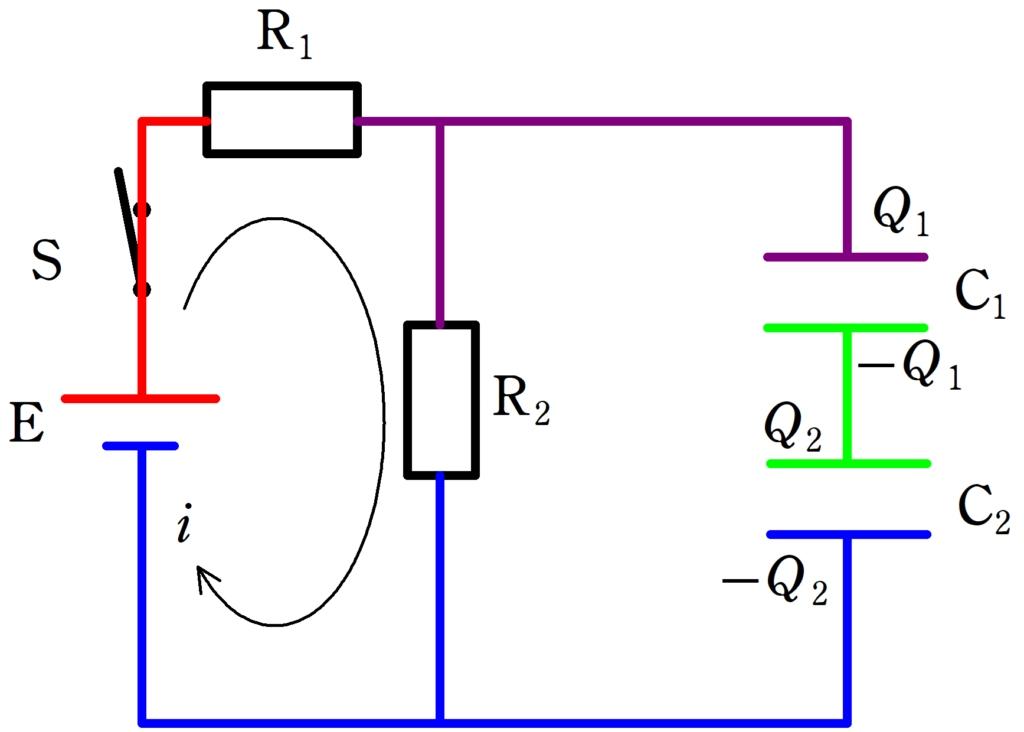
★　キルヒホッフ則

抵抗$\rm R_{1}$，$\rm R_{2}$に流れる電流を$i$として

$V=Ri+2Ri$

$\therefore　i=\dfrac{V}{3R}$

NEKO

すると，$\rm R_{1}$について，オームの法則より

$R\cdot i=\dfrac{V}{3}$

の電位差が生じます．

上図の青色部分の電位を基準の0とすると，赤い部分は$V$，紫の部分は

$V-\dfrac{V}{3}=\dfrac{2}{3}V$

となります．

NEKO

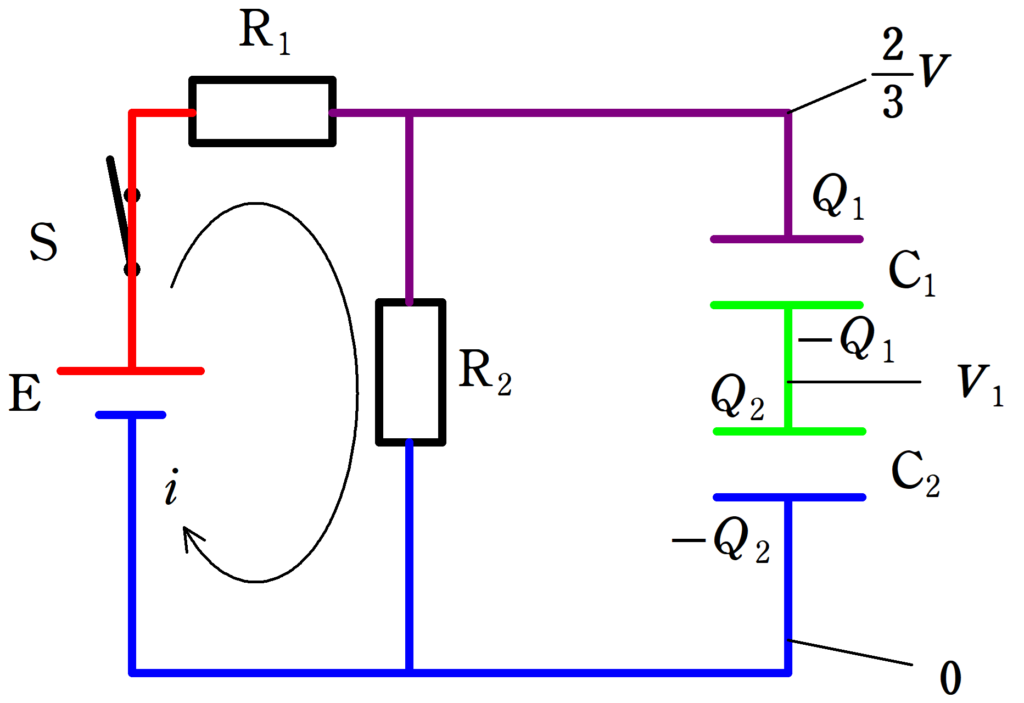
緑色部分の電荷保存則と，$\rm C_{1}$，$\rm C_{2}$のコンデンサーの式を立てます．

電荷と電位は上図のように設定しましょう．緑色部分の電位を$V_{1}$としています．

★　電荷保存則

$-Q_{1}+Q_{2}=0$　$\therefore　Q_{1}=Q_{2}$　$\dots　(\ast)$

★　コンデンサーの式

$Q_{1}=C(\dfrac{2}{3}V-V_{1})$　$\dots　(2\ast)$

$Q_{2}=2CV_{1}$　$\dots　(3\ast)$

NEKO

$Q_{1}=C(V-V_{1})$としないように注意してね．

このようなミスをなくすには，はじめから次のような式を立てるのも一つだよ．

$V-Ri-\dfrac{Q_{1}}{C}-\dfrac{Q_{2}}{2C}=0$

$V-Ri-2Ri=0$

さて，さきほどの計算にもどりましょう．

$(2\ast)$と$(3\ast)$を$(\ast)$に代入して，$V_{1}$を求めましょう．

$(\ast)$より

$C(\dfrac{2}{3}V-V_{1})=2CV_{1}$

$\therefore　V_{1}=\dfrac{2}{9}V$

これを$(2\ast)$，$(3\ast)$に代入して

$\eqalign{Q_{1}&=C(\dfrac{2}{3}V-\dfrac{2}{9}V)\\&=\dfrac{4}{9}CV}$

$Q_{2}=\dfrac{4}{9}CV$

NEKO

答えは，$Q_{1}=Q_{2}=\dfrac{4}{9}CV$です．

今回は電位による解法をとりましたが，このくらいのコンデンサーの数であれば，キルヒホッフ則を使う方が確実に解けるので挑戦してみてください．