<解答>
(1)
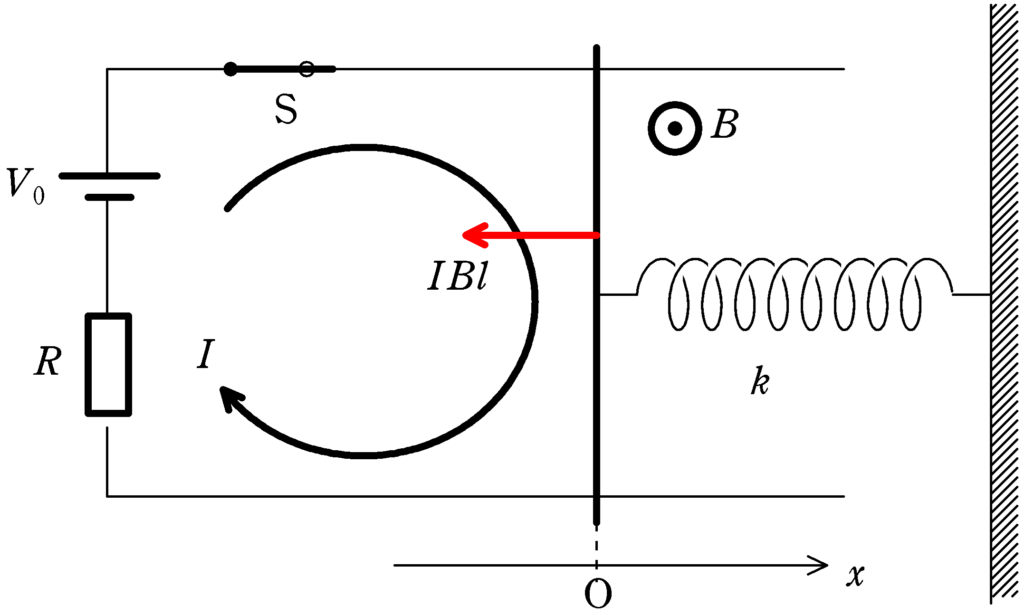
回路に流れる電流を$I$として,キルヒホッフの第2法則より
$V_{0}-RI=0$ $I=\dfrac{V_{0}}{R}$ (答)
また,導体棒には図の下方向に電流が流れており(左手中指),磁場は奥から手前(左手人差し指)なので,フレミング左手の法則より,電磁力は図の左向きにはたらく(左手親指).
また,電磁力の大きさは$IBl=\dfrac{V_{0}Bl}{R}$なので,電磁力$F_{0}$は
$F_{0}=-\dfrac{V_{0}Bl}{R}$ (答)
$F_{0}=\dfrac{V_{0}Bl}{R}$とする人が多いので注意!
(2)
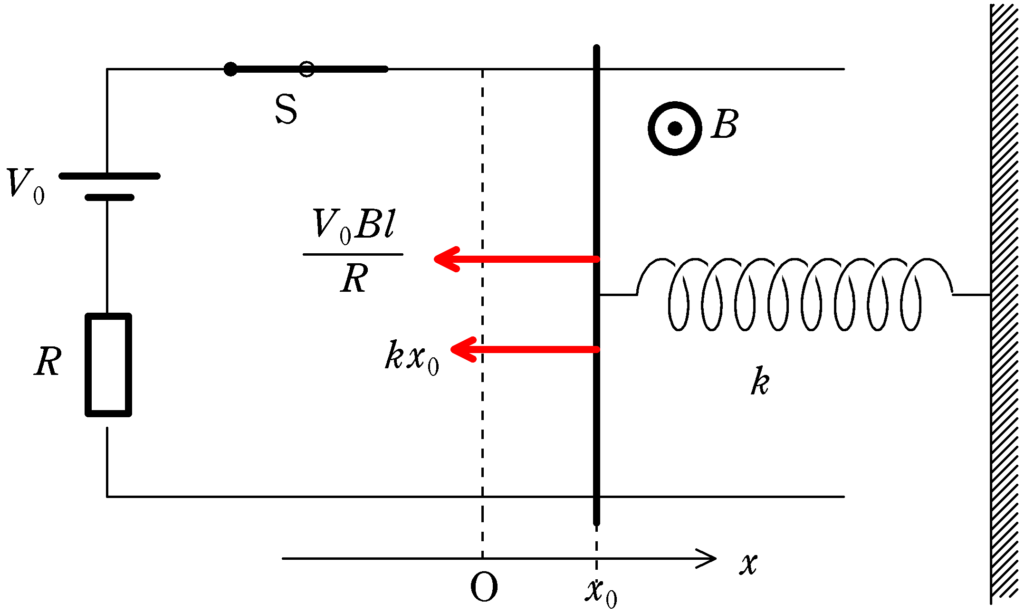
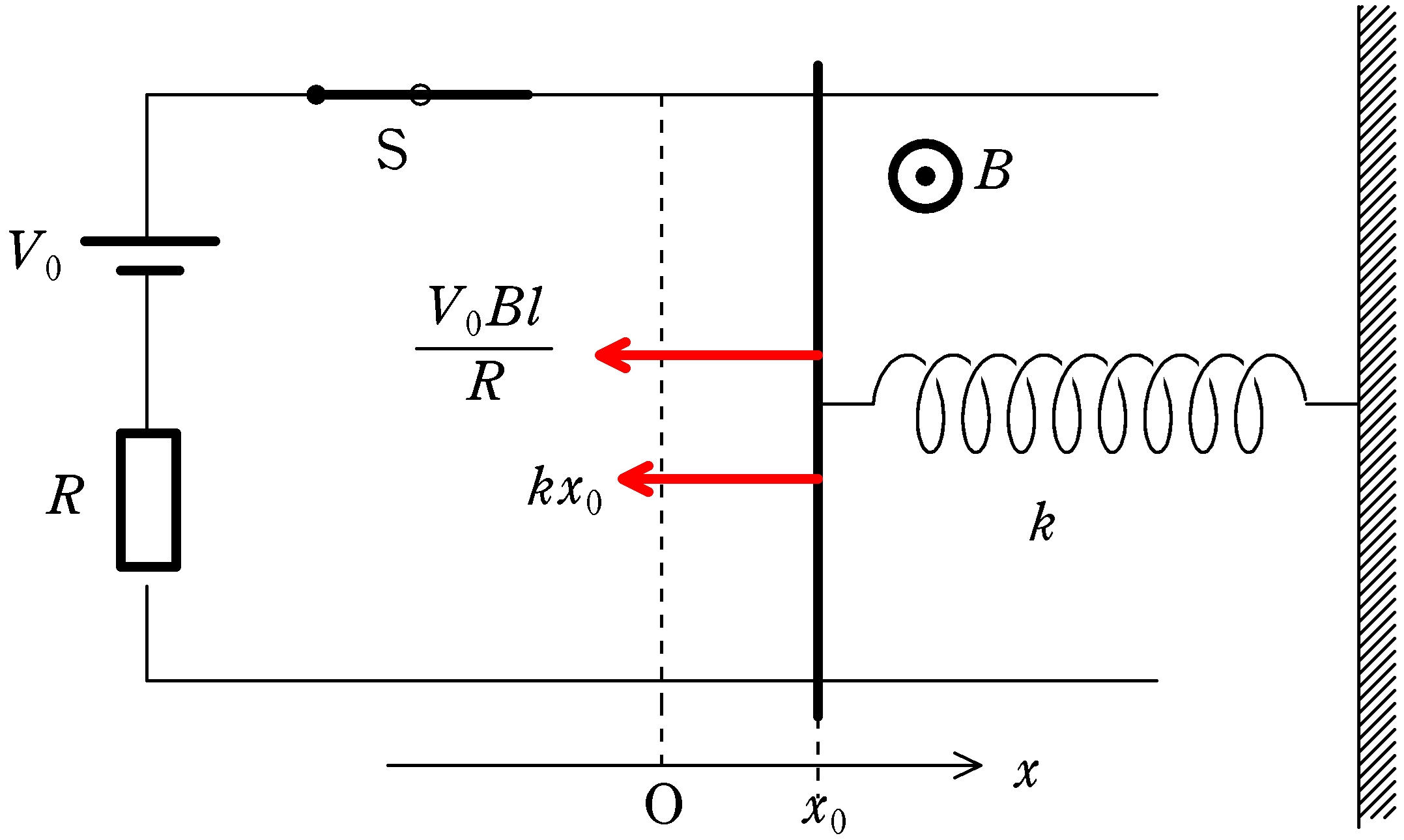
$x=x_{0}$に導体棒があるときの力のつり合いの式を立てる.
上図は$x_{0}>0$の位置に導体棒がある状態になっている.このとき,ばねは$x_{0}$縮んでいて,伸びる方向,つまり負の方向に弾性力がはたらく.弾性力は$-kx_{0}$.
もし,$x_{0}<0$であれば,ばねは$|x_{0}|=-x_{0}$伸びていて,弾性力はばねが縮む方向,つまり,正方向にはたらく.弾性力は$+k\times (-x_{0})=-kx_{0}$
つまり,$x_{0}$が正であれ,負であれ,弾性力は$-kx_{0}$.
一方,(1)より,電磁力は$F_{0}=-\dfrac{V_{0}Bl}{R}$であるから,導体棒のつり合いの式より
$-kx_{0}-\dfrac{V_{0}Bl}{R}=0$ $\therefore\,\, x_{0}=-\dfrac{V_{0}Bl}{kR}$(答)
※これも$x_{0}=\dfrac{V_{0}Bl}{kR}$と答える人が多い.

コメント