
熱力学演習のはじまりです!
今回の内容は定圧変化.
熱力学の問題は,公式が多くて大変ですよね.
また,どのような変化なのかを判断するのが意外と難しいんです.
この熱力学演習シリーズでは,
・公式の立て方
・変化の見極め方
の話もしていきます.
それでは,問題がみていきましょう.
問題文には,番号が振ってあります.その番号の読み取り方も含めて解説していきます.
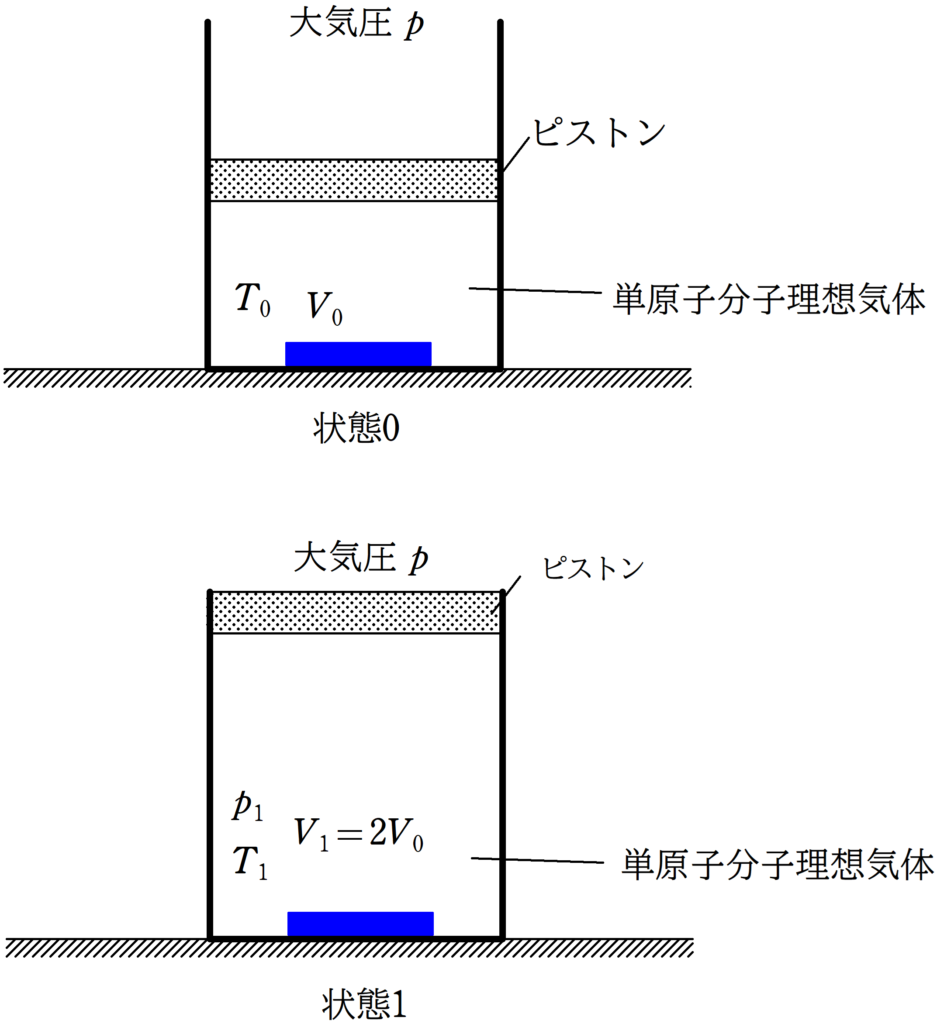
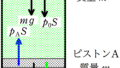
上図のように,水平な床の上に①断熱容器が固定されている.
また,②なめらかなに動く質量$m$で断面積$S$の熱を通さないピストンによって,③単原子分子理想気体が封入されている.
はじめ,単原子分子理想気体の体積は$V_{0}$,絶対温度は$T_{0}$であった.この状態を状態0とする.
断熱容器の底には,温度調節器があり,この温度調節器によって,単原子分子理想気体を④ゆっくりとあたためていったところ,ピストンは④ゆっくりと上昇し,単原子分子理想気体の体積が$2V_{0}$になったところで,温度調節器を止めた.
このときの状態を状態1とする.
大気圧を$p$とし,重力加速度の大きさを$g$とする.次の問いに答えよ.
(1) 状態0における,気体の圧力$p_{0}$を求めよ.
(2) 状態1における,気体の圧力$p_{1}$,絶対温度$T_{1}$をそれぞれ求めよ.
(3) 状態0から状態1の間に気体がした仕事$W$,内部エネルギーの変化$\Delta U$,気体が吸収した熱量$Q$をそれぞれ求めよ.
<用語の解説>
①断熱容器:熱を通さない容器.今回は温度調節器以外での熱の出入りはない.
②なめらかなに動く:摩擦力ははたらかない.
③単原子分子理想気体:定圧モル比熱が$\dfrac{3}{2}R$($R$は気体定数)となる.すなわち,次のことがいえる.
問題分に単原子分子理想気体とかいてあるときは,次のことを使うことができる.
定積モル比熱が$\dfrac{3}{2}R$である.すなわち
内部エネルギー$U$は
$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$
内部エネルギーの変化$\Delta U$は
$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$
※$n$:物質量,$T$:絶対温度,$p$:圧力,$V$:体積
④ゆっくり:準静的変化を行う.すなわち,ピストンは常につり合いながら移動する.

物理の問題は,用語の中に深い意味が隠されているだね.
それでは,解答にいきましょう.
<解答>

熱力学の問題を解くときは,次の3つの式を立てることを心掛けるとよいでしょう.
- 可動部分のつり合いの式 → 力の情報が出てくる
- 理想気体の状態方程式(ボイルシャルルの法則)
- 熱力学第一法則 → エネルギーの情報が出てくる
(1)

まずは,
1.可動部分のつり合いの式
だね.
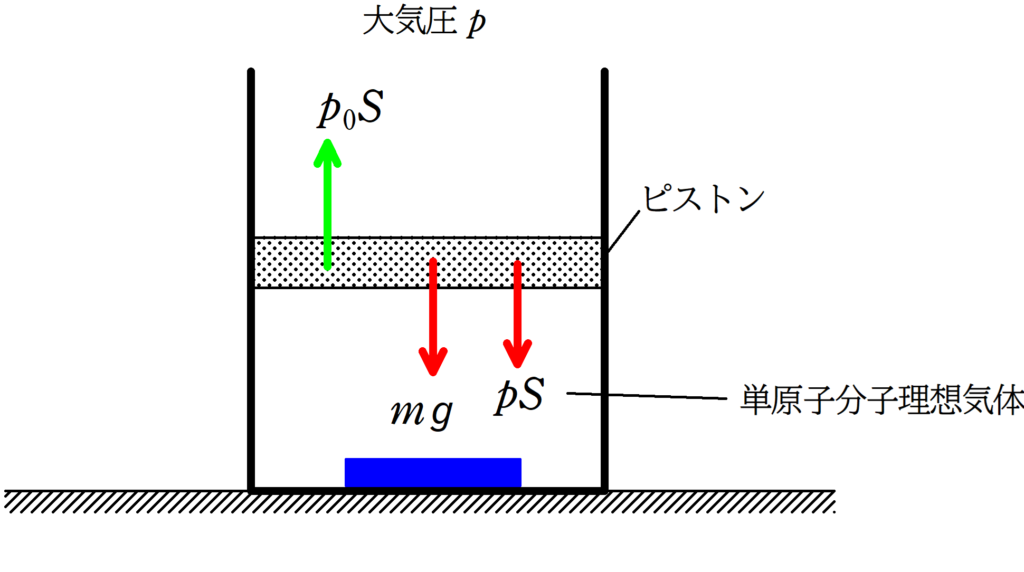
今回,動くのはピストンなので,ピストンのつり合いの式を立てます.
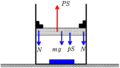
ピストンにはたらく力は,
重力:$mg$
大気がおす力:$pS$
単原子分子がおす力$p_{0}S$
があります.
★ ピストンのつり合いの式
$p_{0}S=pS+mg$
$\therefore$ $p_{0}=p+\dfrac{mg}{S}$

気体の圧力は,外部の力の情報によって決定するんだね.
もし,外部の力の情報が変化しなかったら,気体の圧力は変化しないよ.
今回は,重力$mg$は変化しないし,大気圧$p$も変化しないので,気体の圧力は変化しません.
このように,圧力が変化しないことを定圧変化といいます.
(2)

次に状態1に圧力$p_{1}$と絶対温度$T_{1}$をもとめます.
定圧変化なので,$p_{1}=p_{0}=p+\dfrac{mg}{S}$ですね.
そして,絶対温度は
2.理想気体の状態方程式(ボイルシャルルの法則)
を立てます.
理想気体について,物質量$n$が変化しないとき,気体の圧力を$p$,気体の体積を$V$,絶対温度を$T$とすると,
$\dfrac{pV}{T}=$一定
が成り立つ.(ボイル・シャルルの法則)
特に,温度が一定のとき
$pV=$一定(ボイルの法則)
圧力が一定のとき
$\dfrac{V}{T}=$一定(シャルルの法則)
が成り立つ.

定圧変化なので,シャルルの法則を立てます.
★ シャルルの法則
$\dfrac{V_{0}}{T_{0}}=\dfrac{2V_{0}}{T_{1}}$
$\therefore$ $T_{1}=2T_{0}$
(3)

気体がした仕事は$pV$グラフを利用しましょう.

定圧変化なので,縦軸が圧力$P$,横軸が体積$V$のグラフはヨコ線となりますね.
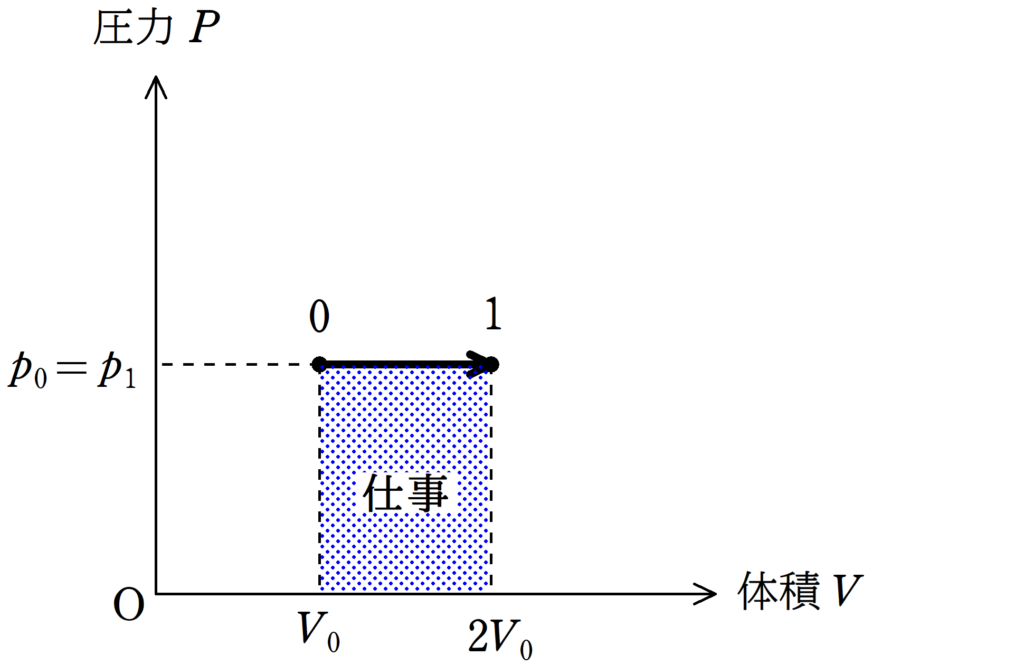

このとき,上図の青色部分の面積が気体がした仕事です.
つまり,気体がした仕事$W$は
$\eqalign{W&=p_{0}(2V_{0}-V_{0})\\&=(p+\dfrac{mg}{S})V_{0}}$

さらに,内部エネルギーの変化$\Delta U$は
$\eqalign{\Delta U&=\dfrac{3}{2}(p_{1}\cdot 2V_{0}-p_{0}V_{0})\\&=\dfrac{3}{2}p_{0}V_{0}\\&=\dfrac{3}{2}(p+\dfrac{mg}{S})V_{0}}$
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$

仕上げの熱量$Q$は
3.熱力学第一法則
を用いて,計算します.
★ 熱力学第一法則
$\eqalign{Q&=\Delta U+W\\&=\dfrac{3}{2}(p+\dfrac{mg}{S})V_{0}+(p+\dfrac{mg}{S})V_{0}\\&=\dfrac{5}{2}(p+\dfrac{mg}{S})V_{0}}$
以上より,$W=(p+\dfrac{mg}{S})V_{0}$,$\Delta U=\dfrac{3}{2}(p+\dfrac{mg}{S})V_{0}$,$Q=\dfrac{5}{2}(p+\dfrac{mg}{S})V_{0}$

これから様々なパターンの演習問題を解いていきましょう.


コメント
[…] […]