
今回はニュートン環の問題です.
経路差を求める際に近似式を使うので,慣れておきましょう.
$|\alpha|\ll1$のとき
$(1+\alpha)^n\fallingdotseq 1+n\alpha$

問題文では
$a\ll b$ や $b$ は $a$ に比べて十分大きい
のような表現をします.これを
$\dfrac{a}{b}\ll1$
として,小さい数を作りましょう.このとき,$\alpha =\dfrac{a}{b}$と対応します.
さて,問題です!
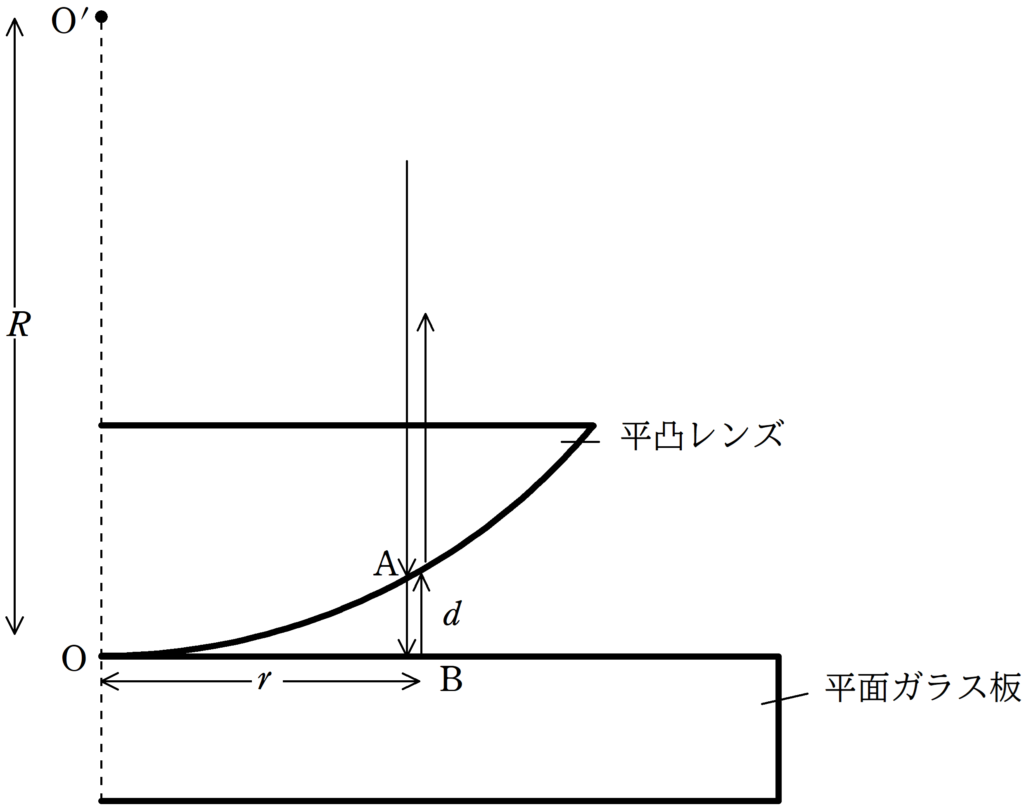
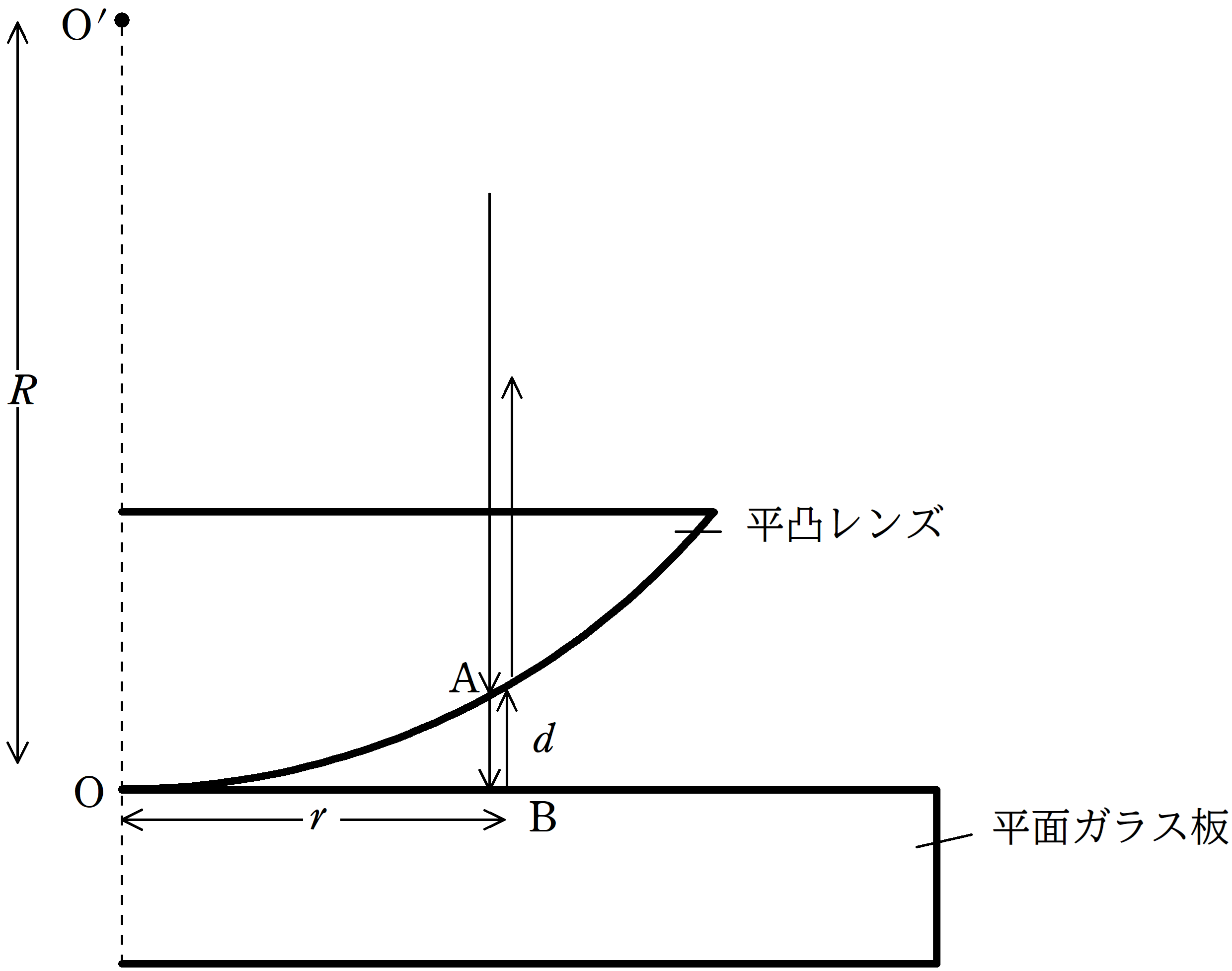
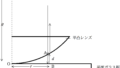
図のように,厚い平面ガラス板の上に平凸レンズを置く.レンズは中心の位置Oでガラス板と接触していて,ガラス板の平面とレンズの平面は平行になっている.レンズの平面側の上方から波長$\lambda$の単色光を平面に直角に照射して,レンズの平面側から眺める.すると,光の明暗の線が同心円状に交互に観測される.レンズの中心線からの距離を$r$,その位置でのレンズとガラス板の間の空気層の厚みを$d$とする.レンズの曲面は中心を$\rm O^{\prime}$とする曲率半径$R$の球面の一部とみなす.空気に対するレンズおよびガラス板の屈折率を$n$とし,$R$は,$r$に比べて十分大きいとする.このとき,次の問いに答えよ.
(1) $d$を$R$,$r$を用いて表せ.ただし,この問いでは,近似をしなくてもよい.
(2) $|\alpha|\ll1$のとき,$(1+\alpha)^{n}\fallingdotseq1+n\alpha$の近似式を使って,$d$を$R$,$r$を用いて表せ.
<解答>
(1)

Aから線分$\rm OO^{\prime}$に垂線を下し,その交点をHとします.
$\rm \bigtriangleup AO^{\prime}H$について,三平方の定理より
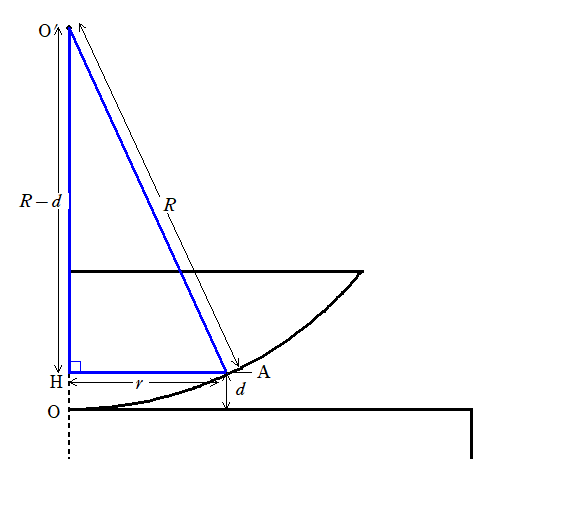
$(R-r)^{2}+r^{2}=R^{2}$
$d=R-\sqrt{R^{2}-r^{2}}$(答) $(\because R>d)$
(2)

(1)の結果を近似式を使って計算しましょう.
$|\alpha|\ll1$のとき
$(1+\alpha)^n\fallingdotseq 1+n\alpha$
$\eqalign{d&=R-R\sqrt{1-\left(\dfrac{r}{R}\right)^{2}}\\&\fallingdotseq R-R\left\{1-\dfrac{1}{2}\left(\dfrac{r}{R}\right)^{2}\right\}\\&=\dfrac{r^{2}}{2R}}$

したがって,答えは,$d=\dfrac{r^{2}}{2R}$(答)

コメント
[…] […]
[…] 経路差は$2d=dfrac{r^{2}}{R}$です.(こちらでで確認してください.) […]