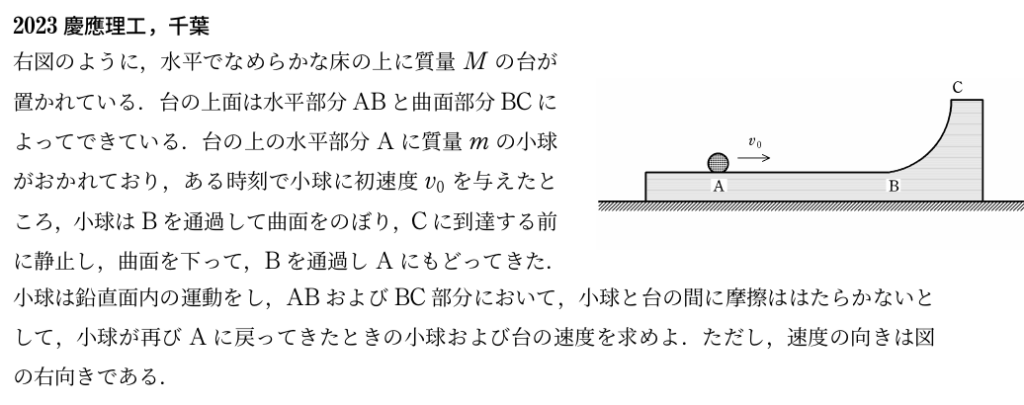
<問題>
<解答>
まずは,標準的な解法から紹介します。
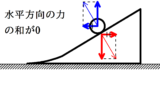
小球と台を対象物体にすると水平方向の力の和は$0$なので,水平方向の運動量が保存します.
また,台と床,台と小球の間には摩擦力ははたらかず,その他の外力も仕事をしていないので,台と小球を対象物体としたときの力学的エネルギーが保存します.(小球だけでは力学的エネルギーは保存しません.)
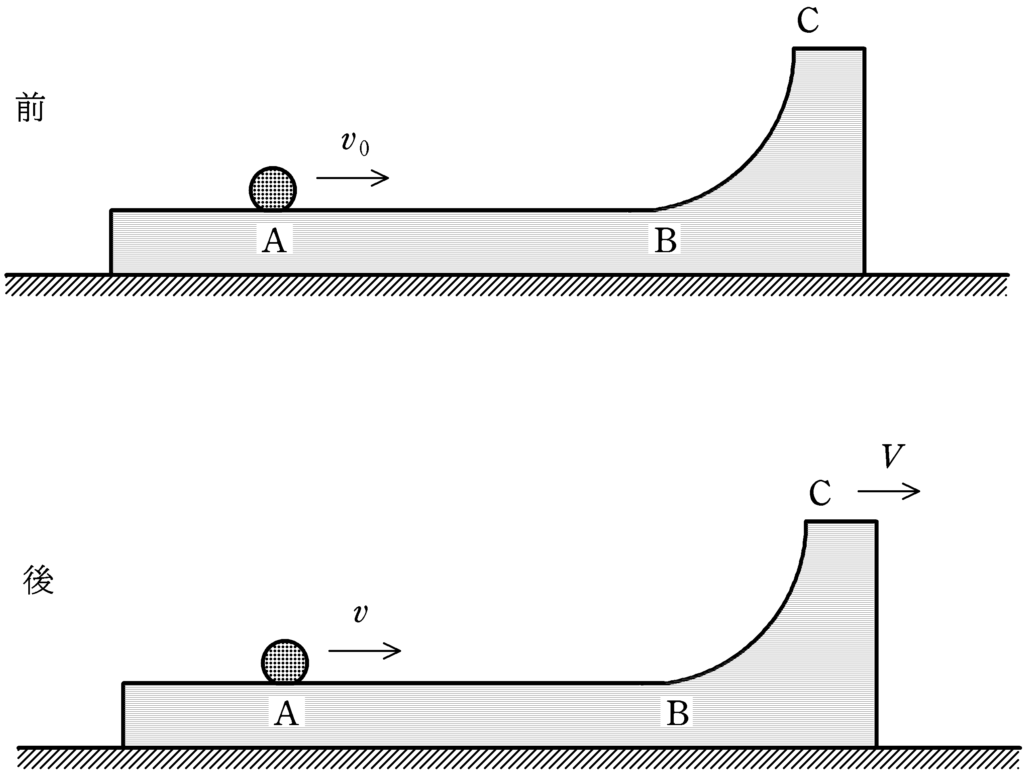
小球が再びAにもどってきたときの小球の速度と台の速度(速さではない)をそれぞれ$v,V$として,運動量保存則,力学的エネルギー保存則を立てて
\begin{align} \begin{cases} mv_{0}=mv+MV &\cdots (\ast)\\ \dfrac{1}{2}mv_{0}^{2}=\dfrac{1}{2}mv^{2}+\dfrac{1}{2}MV^{2} &\cdots (2\ast) \end{cases} \end{align}
$(\ast)$より,$V=\dfrac{m(v_{0}-v)}{M} \cdots (3\ast)$として,$(2\ast)$に代入すると
\begin{align} \cancel{\dfrac{1}{2}}mv_{0}^{2}&=\cancel{\dfrac{1}{2}}mv^{2}+\cancel{\dfrac{1}{2}}M\left(\dfrac{m(v_{0}-v)^{2}}{M}\right)\\ \cancel{m}v_{0}^{2}&=\cancel{m}v^{2}+\dfrac{m^{\cancel{2}}(v_{0}^{2}-2v_{0}v+v^{2})}{M} \end{align}
両辺$M$をかけて
\begin{align} &Mv_{0}^{2}=Mv^{2}+mv_{0}^{2}-2mv_{0}v+mv^{2}\\ &\therefore\,\, (M+m)v^{2}-2mv_{0}v+(m-M)v_{0}^{2}=0\\ &\therefore\,\,\left\{(M+m)v-(m-M)v_{0}\right\}(v-v_{0})=0 \end{align}
したがって,$v=\dfrac{m-M}{M+m}v_{0}$または$v=v_{0}$だが,$v=v_{0}$だと$(3\ast)$に代入したとき$V=0$になってしまう.小球が曲面上にあるとき,台は小球に常に右方向に力を加えられているため,正の運動量を持っているはず.したがって,$V>0$.したがって,$v=\dfrac{m-M}{M+m}v_{0}$(答)(本当はこの$V>0$を調べていないので,この段階では断定できない.)
ちなみに,$m$と$M$の大小で$v$の速度の方向がかわる.$v=\dfrac{m-M}{M+m}v_{0}$を$(3\ast)$に代入して
\begin{align} V&=\dfrac{m}{M}\left(v_{0}-v\right)\\ &=\dfrac{m}{M}\left(v_{0}-\dfrac{m-M}{M+m}v_{0}\right)\\ &=\dfrac{mv_{0}}{M}\times \dfrac{M+m-(m-M)}{M+m}\\ &=\dfrac{2mv_{0}}{M+m} \end{align}
したがって,$V=\dfrac{2mv_{0}}{M+m}$(答)
<別解>
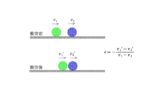
小球が曲面をのぼり,おりてくるときに力学的エネルギーが保存しています.これを弾性衝突として考え,問題を解くこともできます.
衝突の問題のとき,反発係数は相対速度の大きさの比であることを利用する.
つまり,台からみると速度が$-1$倍になるので,$-v_{0}$になる.
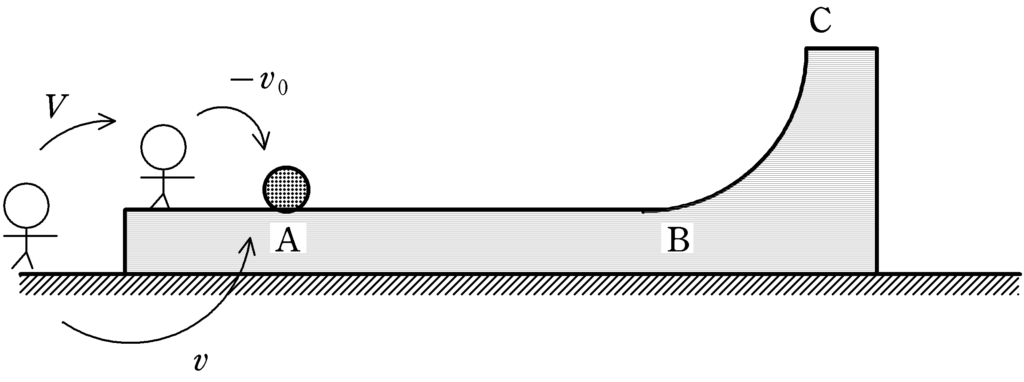
$V+(-v_{0})=v$ $\cdots (4\ast)$
これを用いれば,$(\ast)$と$(4\ast)$を連立して,より簡単に計算することができる.





コメント