twitterの問題13の解答

<解答>

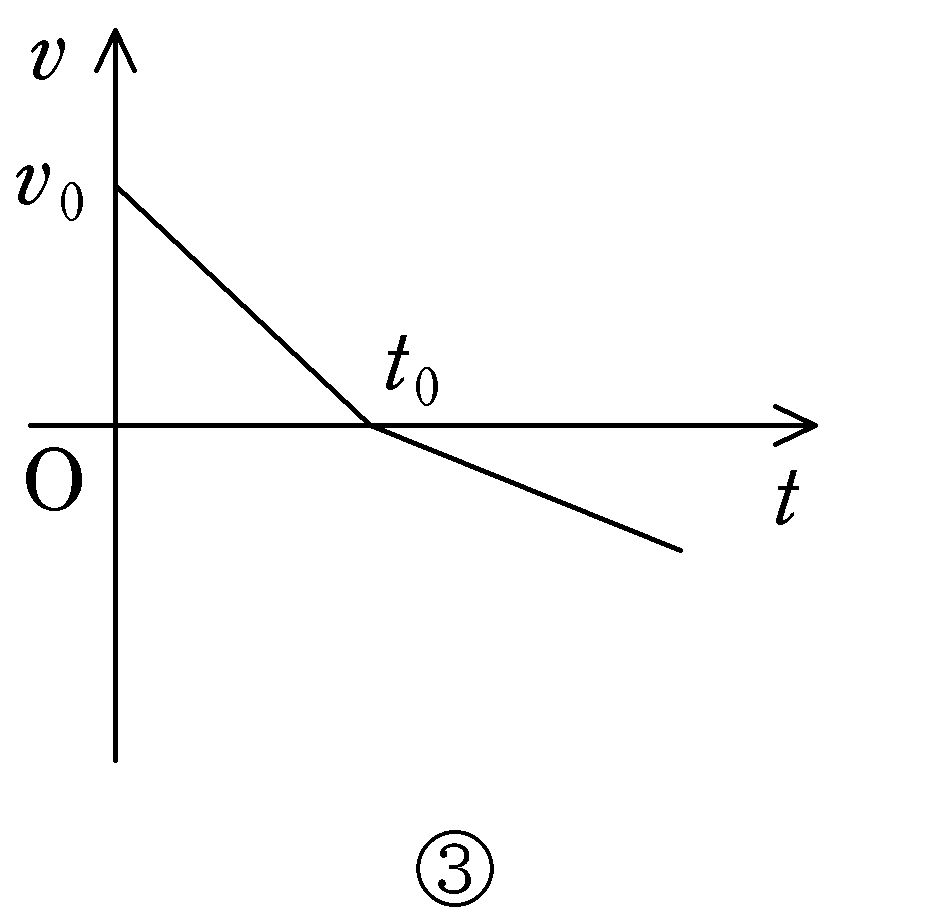
④，⑤，⑥は$t=t_{0}$で静止した後の速度がまた正になっているから，さらに上り続けることになる．これは問題文の条件に合わない（そもそも起こりえないが）ので不適．

すると，①，②，③のどれかになる．最高点に達した後，傾きが変化するのか変化しないのか，変化するとしたら，どのように変化するのかがわかれば選択肢を選ぶことができる．

$v-t$グラフの傾きは加速度である．したがって，運動方程式を立てて，加速度を求めることからはじめる．その際，物体がのぼっているときは，動摩擦力は斜面下方向にはたらき，物体がくだっているときは，動摩擦力は斜面上方向にはたらくことに注意．

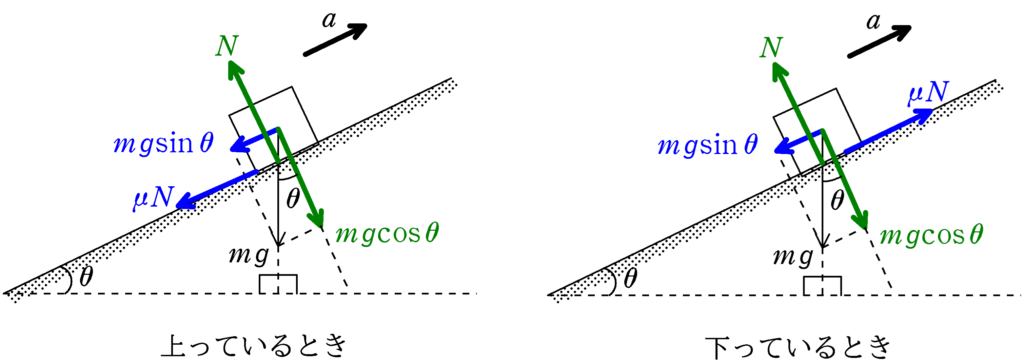
また，物体の質量を$m$，重力加速度の大きさを$g$とする．

上っているときも下っているときも斜面垂直方向のつり合いの式を立てると，垂直抗力の大きさ$N$は

$N=mg\cos\theta$

である．

★上っているときの運動方程式

斜面上方向に加速度$a_{1}$をとる．

$ma_{1}=-mg\sin\theta-\mu N=-(\sin\theta+\mu \cos\theta)mg$

$\therefore\,\,a_{1}=-(\sin\theta+\mu \cos\theta)g$　$\cdots (\ast)$

★下っているときの運動方程式

斜面上方向に加速度$a_{2}$をとる．

$ma_{2}=-mg\sin\theta+\mu N=-(\sin\theta-\mu \cos\theta)mg$

$\therefore\,\, a_{2}=-(\sin\theta-\mu \cos\theta)g$　$\cdots (2\ast)$

$\mu<\tan\theta$なので，$\mu<\dfrac{\sin\theta}{\cos\theta}$，つまり$\mu\cos\theta<\sin\theta$なので，$a_{2}<0$である．すると，それぞれの加速度の大きさは

$|a_{1}|=(\sin\theta+\mu \cos\theta)g$

$|a_{2}|=(\sin\theta-\mu \cos\theta)g$

より，$|a_{1}|>|a_{2}|$となり，下っているときは上っているときより傾きがゆるやかになる．

以上のことを踏まえると，一番適するものは③（答）である．