
前回は,
導体棒が動く→導体棒が電池になって回路に電流を流す
という練習問題を扱いました.
今回は,摩擦力がある場合の問題です.
次の2つをいまいちど確認しておきます!
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式

それでは,演習問題を解いてみましょう!
前回の内容はこちら!
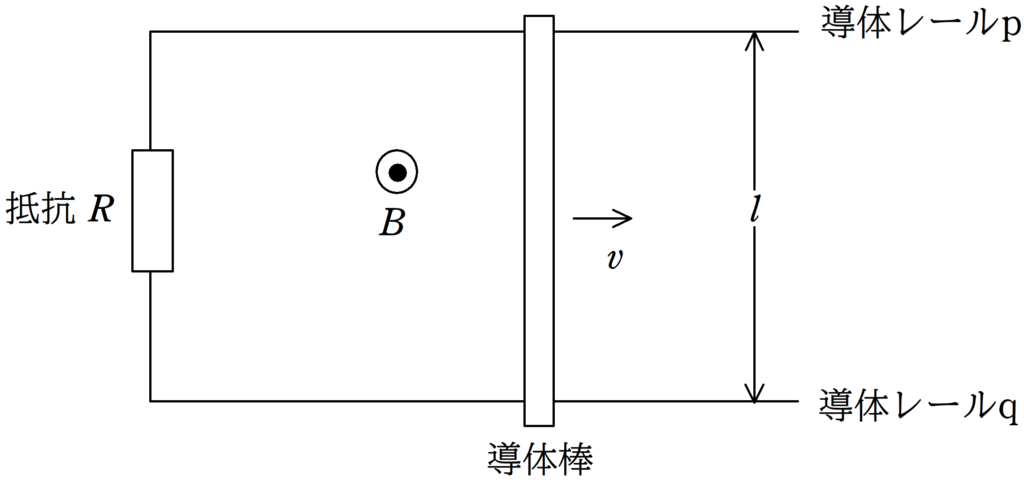
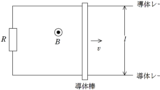
図のように,平行に固定された導体レールp,qと抵抗値$R$の抵抗と長さ$l$で一様な密度の質量$m$の導体棒を用いて回路をつくった.
いま,画面奥から手前向きに一様な磁束密度$B$の磁場をかけた状態で導体棒を右方向に速さ$v$で等速直線運動させた.
抵抗値$R$以外の抵抗は無視をし,空気抵抗も無視をする.また,導体棒とレールの間には動摩擦力がはたらき,動摩擦係数を$\mu$とし,重力加速度の大きさを$g$とする.
(1) 導体棒に流れる電流の大きさを求めよ.
(2) 導体棒を等速度運動させるために外力を加えている.この外力の大きさと向きを答えよ.
(3) 抵抗で単位時間あたりに生じるジュール熱を求めよ.
<解答>
(1)
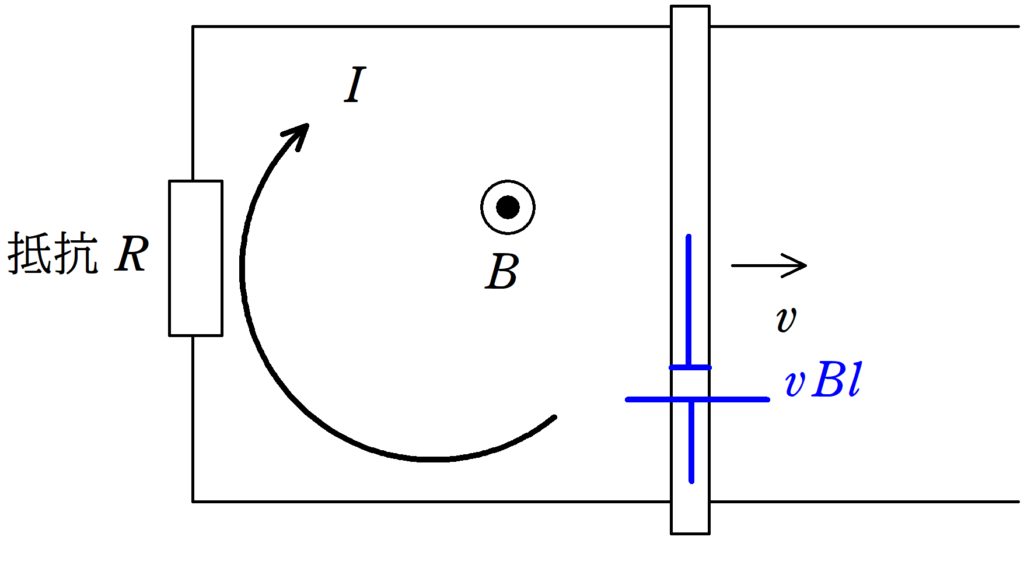
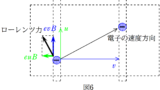
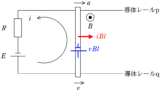
導体棒が磁場中を動くので電池になります.
電池の起電力は$vBl$,向きは上図のようになります.
回路に流れる電流を$I$とすると,オームの法則より
$vBl=RI$ $\therefore I=\dfrac{vBl}{R}$
したがって,回路に流れる電流の大きさは$\dfrac{vBl}{R}$です.
(2) 導体棒は等速度運動しています.速度が変化していないので,加速度0です.
運動方程式$ma=F$からもわかる通り,$a=0$のとき$F=0$となります.
つまり,導体棒にはたらく力の和は0ということです.
導体棒にはたらく力をすべてかいてみましょう.
★導体棒にはたらく鉛直方向の力
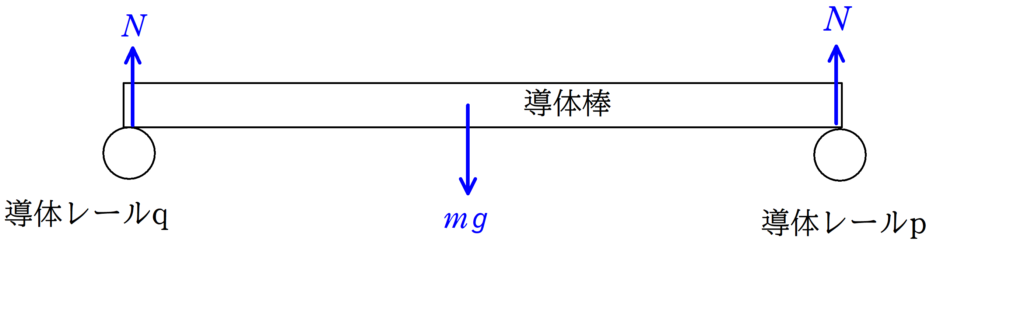
上図は導体棒の進行方向から眺めたときのものです.
導体棒にはたらく力は重力と各導体レールとの間の垂直抗力があります.
今回は導体棒が一様な密度であるから重力は導体棒の中心にはたらき,導体レールp , qには,同じ大きさの垂直抗力がはたらきます.
垂直抗力の大きさを$N$とすれば,鉛直方向のつり合いの式は次のようになります.
$N+N=mg$ $\therefore N=\dfrac{1}{2}mg$ $\dots (\ast)$
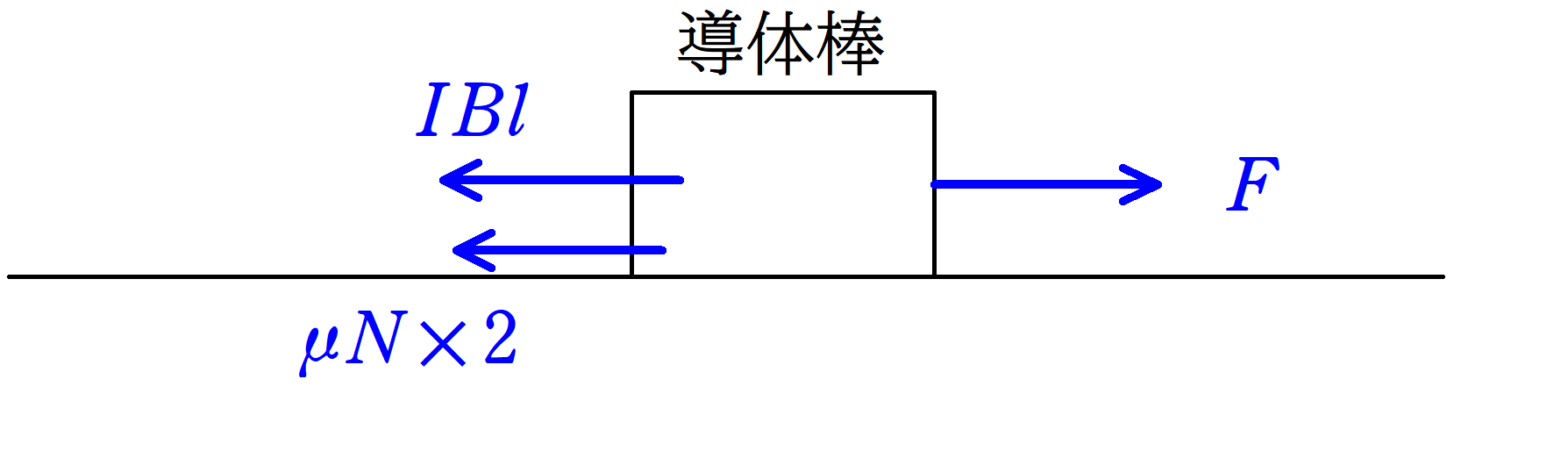
★導体棒にはたらく水平方向の力
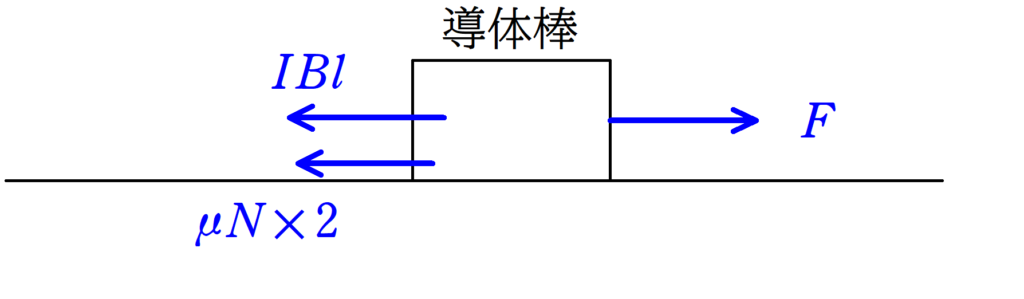
導体棒に水平方向にはたらく力は外力$F$と,電流が磁場から受ける電磁力$IBl$,動摩擦力$\mu N \cdot 2$です.
水平方向のつり合いの式より
$F=IBl+2\mu N$
$(\ast)$と(1)の結果である,$I=\dfrac{vBl}{R}$より
$\eqalign{F&=\dfrac{vBl}{R}\cdot Bl +2\mu \cdot \dfrac{1}{2}mg\\&=\dfrac{vB^{2}l^{2}}{R}+\mu mg}$
したがって,外力の力は右方向に大きさ$\dfrac{vB^{2}l^{2}}{R}+\mu mg$となります.

よく,動摩擦力が2箇所にかかるから,$2\mu mg$とする人をみるよ.
そのようにしてしまう人は,$N=mg$と考えてしまう傾向があるので,要注意!
垂直抗力はつり合いの式や運動方程式で求めましょう!
(3) 最後に単位時間あたりに生じるジュール熱です.

今回も2通りの方法で計算してみましょう!
・単位時間あたりに抵抗で消費するジュール熱の式を用いる.
抵抗にかかる電圧を$V$,流れる電流を$I$とすると,単位時間あたりに抵抗で消費するジュール熱$P_{1}$は
$P_{1}=VI=vBl\cdot \dfrac{vBl}{R}=\dfrac{(vBl)^2}{R}$
・エネルギー収支の式を立てる.
導体棒と回路のエネルギー収支を考えると
(外力が導体棒にした仕事)+(摩擦力が導体棒にした仕事)=(ジュール熱)

ちなみに,エネルギー収支の式に,電磁力がした仕事や誘導起電力がする仕事を入れない理由は下の記事を読んでね.
単位時間あたりのジュール熱を$P_{2}$としましょう.エネルギー収支の式を立てると
$\eqalign{Fv-\mu mgv&=P_{2}\cr P_{2}&=(\dfrac{vB^{2}l^{2}}{R}+\mu mg)v-\mu mgv\cr P_{2}&=\dfrac{(vBl)^2}{R}}$

やっぱり同じになったね.
ということで(3)の答えは$\dfrac{(vBl)^2}{R}$となります.
次回の内容はこちら.



コメント
[…] […]
[…] […]
[…] […]