[干渉問題]薄膜の干渉3

問題

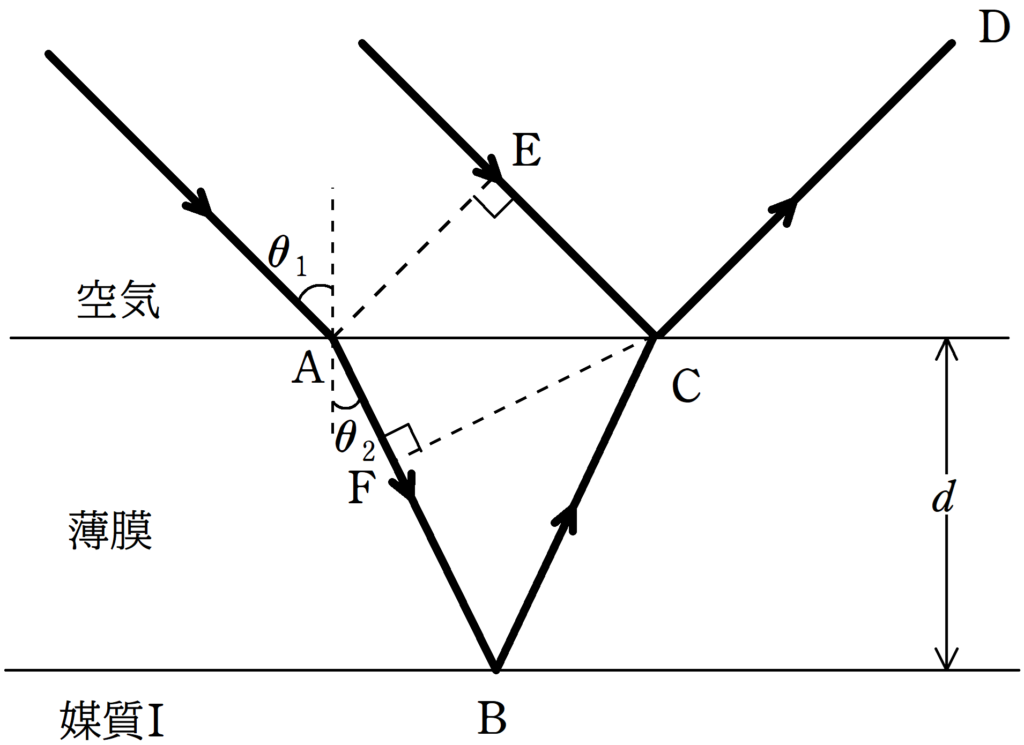
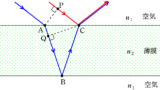
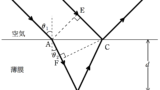
光を薄膜に入射し，反射光の干渉を考える．図のA，Eで位相がそろった波について，Aを通る光は，Fを通過し，媒質Iとの境界であるBで反射し，Cから空気中へ出てDへ行く．一方，Eを通る光はCで反射し，Dに向かい2つの経路の光が干渉する．空気に対する薄膜の屈折率を$n(>1)$とし，A，Cにおける入射角を$\theta_{1}$，Aにおける屈折角を$\theta_{2}$とする．また，薄膜の厚さは$d$であり，空気中の光の波長を$\lambda$とする．このとき，次の問いに答えよ．

(1)　媒質Iが空気のとき，2つの光の強め合いの条件と弱め合いの条件をそれぞれ，$d$，$\theta_{2}$，$\lambda$，$n$，自然数$m$を用いて表せ．

(2)　媒質Iの空気に対する相対屈折率が$n^{\prime}(>n)$のとき，2つの光の強め合いの条件と弱め合いの条件をそれぞれ，$d$，$\theta_{2}$，$\lambda$，$n$，自然数$m$を用いて表せ．

NEKO

CとFは同位相なんだよね．理由はこちらで説明しています．

[薄膜の干渉]位相差が生じる経路の長さ

NEKO 薄膜の干渉の問題で，よく上のような図が出てくるよね． このとき，青い光の経路と赤い光の経路の差は $\rm{ABC-PC}$ だと思っていたんだけど，なぜか問題集の解答では $\rm{QBC}$ の部分を経路差として計算していたん...

physicmath.net

2020.10.08

なので，経路による位相差はFBC部分だけ考えればいいんだね．

NEKO

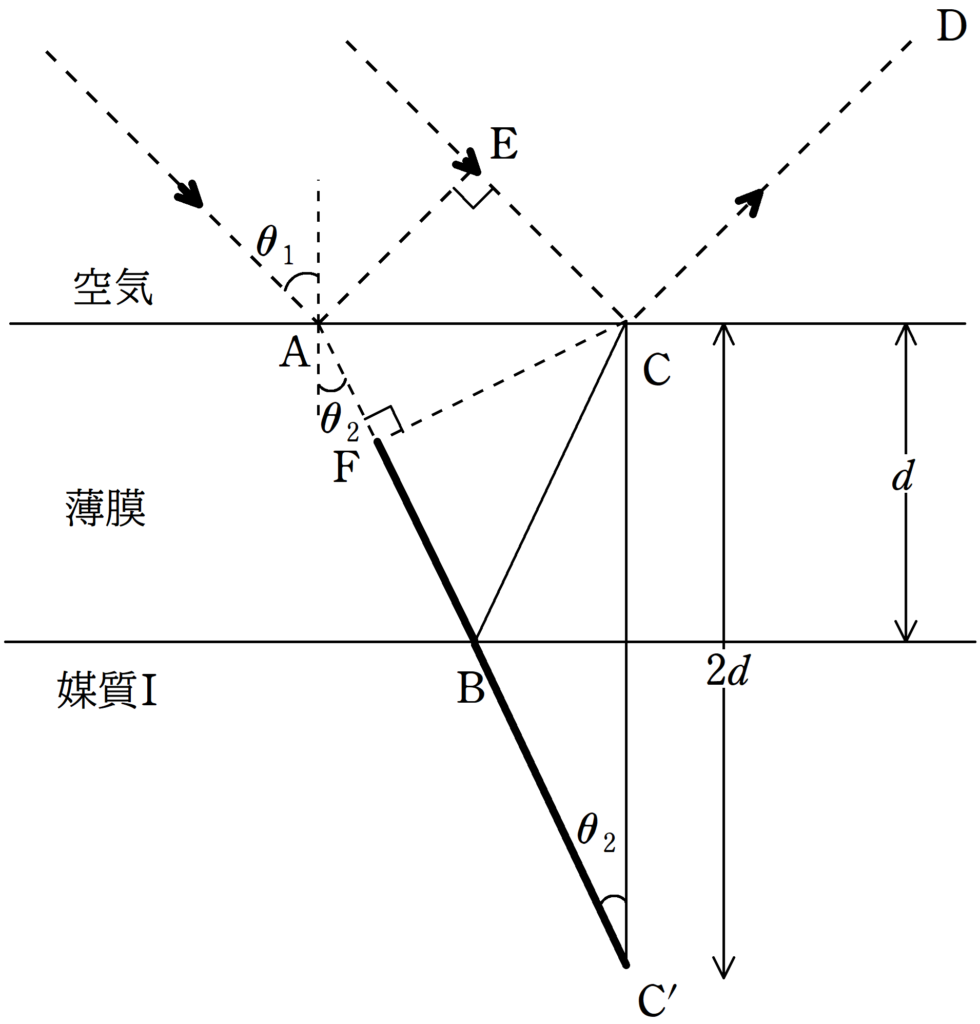
FBCの長さは次のように計算するとよいでしょう．

BCを媒質Iと薄膜の境界線に対して線対称移動したときのCに対応する点を$\rm C^{\prime}$とします．

このとき，$\rm FB+BC=FB+BC^{\prime}$であり，直角三角形$\rm CC^{\prime}F$に着目すると$\rm FC^{\prime}$の長さは

${\rm FC^{\prime}}=2d\cos\theta_{2}$

となります．

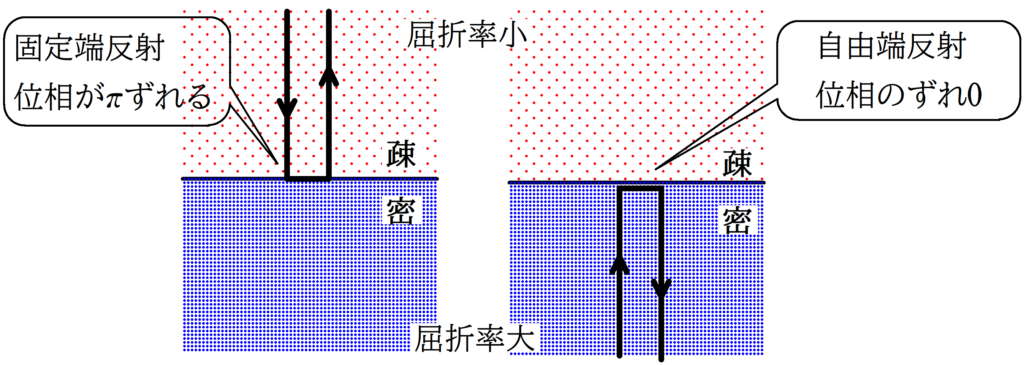
また，Cでは固定端反射，Bでは自由端反射するので，反射による位相差は$\pi$です．

したがって，位相差$\varDelta \varphi$は次のようになります．

$\varDelta \varphi=\dfrac{2\pi}{\dfrac{\lambda}{n}}\cdot 2d\cos\theta_{2}+\pi$

NEKO

ちなみに，位相差は次のことをチェックしましょう．

NEKO

また，固定端反射なのか自由端反射なのかは次の図で確認していきましょう．

強め合いの条件は

$\dfrac{2\pi}{\dfrac{\lambda}{n}}\cdot 2d\cos\theta_{2}+\pi=2\pi m$

$\therefore　\dfrac{4\pi nd\cos\theta_{2}}{\lambda}=(2m-1)\pi$　(答)

弱め合いの条件は

$\dfrac{2\pi}{\dfrac{\lambda}{n}}\cdot 2d\cos\theta_{2}+\pi=(2m+1)\pi$

$\therefore　\dfrac{4\pi nd\cos\theta_{2}}{\lambda}=2m\pi$　(答)

NEKO

今回も右辺には気を付けましょう．

弱め合いの条件の場合，左辺は$\pi$より大きいため，右辺の最小値が$\pi$となってはまずいです．

つまり，$(2m-1)\pi$としてしまうと，$m=1$のとき，$\pi$となってしまうので，よくないですね．

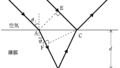
(2)

NEKO

Cでは固定端反射，Bでも固定端反射するので，反射に位相差は0となります．

強め合いの条件は

$\dfrac{2\pi}{\dfrac{\lambda}{n}}\cdot 2d\cos\theta_{2}=2\pi m$

$\therefore　\dfrac{4\pi nd\cos\theta_{2}}{\lambda}=2\pi m$　(答)

弱め合いの条件は

$\dfrac{2\pi}{\dfrac{\lambda}{n}}\cdot 2d\cos\theta_{2}=(2m-1)\pi$

$\therefore　\dfrac{4\pi nd\cos\theta_{2}}{\lambda}=(2m-1)\pi$　(答)

PHYさん

こちらも右辺に注意しましょう．

次回の内容はこちらです．

[干渉問題]薄膜の干渉4

PHYさん 前回の内容はこちらです． 問題がほとんど同じですが，使っていい文字が異なります． 問題 光を薄膜に入射し，反射光の干渉を考える．図のA，Eで位相がそろった波について，Aを通る光は，F，を通過し，媒質Iとの境界であるBで反射し，C...

physicmath.net

2021.06.18