
今回は,等温変化と断熱変化の違いをテーマにした問題です.

それでは,問題を解いてみましょう.
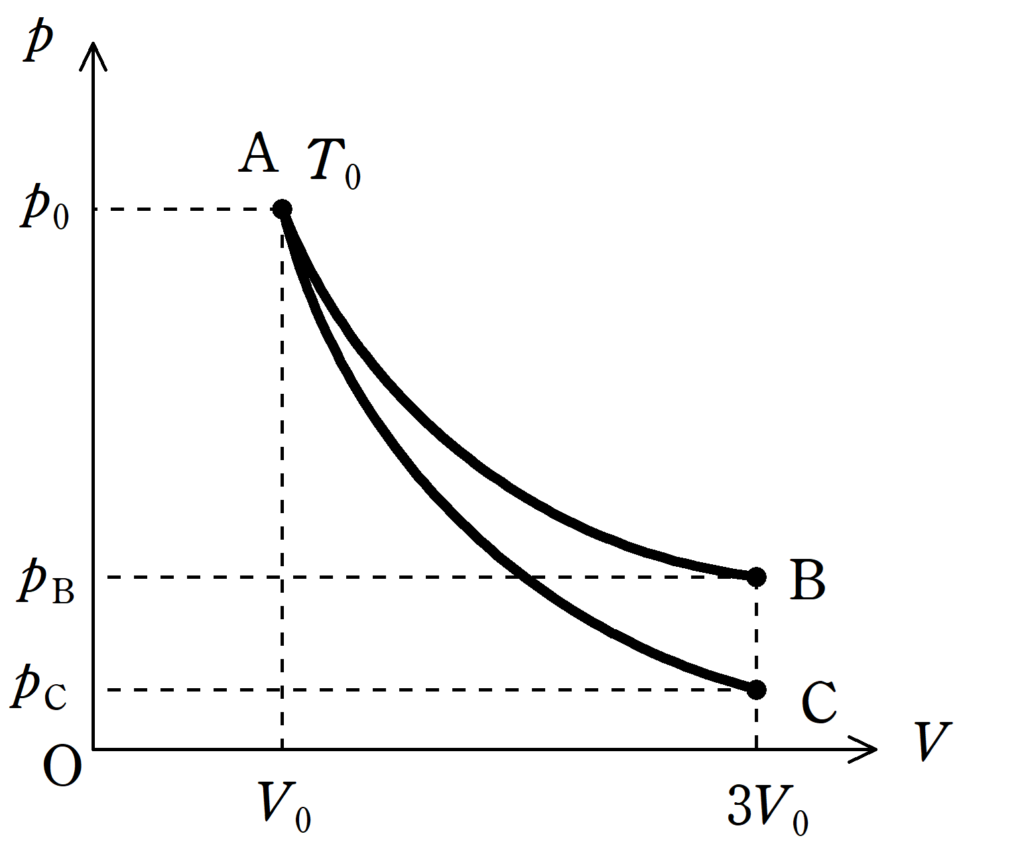
上図のような$pV$図を考える.
状態Aでは,圧力が$p_{0}$で,体積が$V_{0}$,絶対温度が$T_{0}$であった.
次の2つの曲線について考える.
状態Aから温度を一定に保ったまま体積が$3V_{0}$の状態Bに変化させる,曲線AB.
状態Aから気体を断熱したまま体積$3V_{0}$の状態Cに変化させる,曲線AC.
このとき,次の問いに答えよ.
(1) 状態Bにおける温度と状態Cにおける温度では,どちらの方が高いか.
(2) 曲線ABで変化したときの気体がした仕事$W_{\rm AB}$と曲線ACで変化したときの気体がした仕事$W_{\rm AC}$はどちらの方が大きいか.
(3) 状態Bにおける圧力$p_{\rm B}$と状態Cにおける圧力$p_{\rm C}$を$p_{0}$,$V_{0}$,$T_{0}$から適当なものを用いて表せ.ただし,気体は単原子分理想気体であるとしてよい.
<解答>
(1)

温度の大小の読み取りは$pV$図みればすぐにわかりますね.
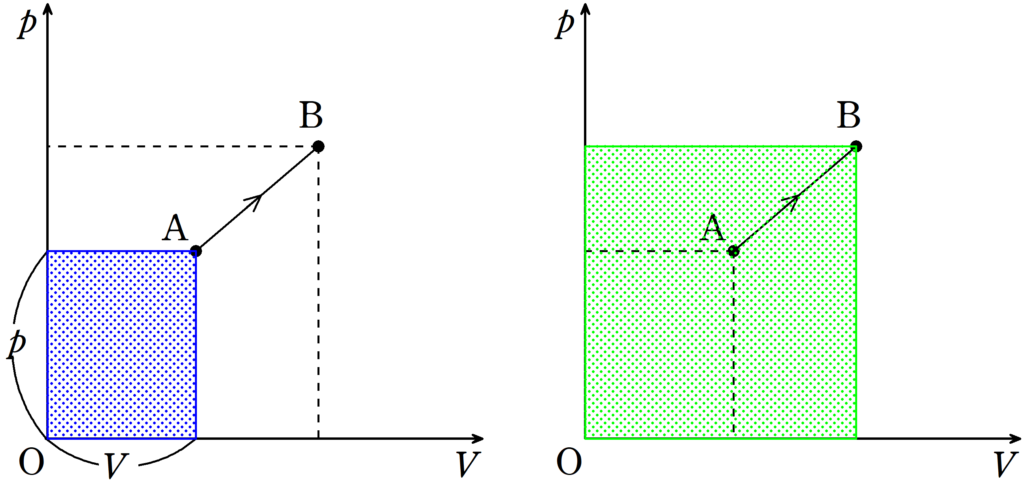
絶対温度は状態の点から$p$軸$V$軸へ下した垂線の足と原点でつくられる長方形の面積に比例する.

曲線AからBは等温変化であるので,OとAによって作られる長方形の面積と,OとBによって作られる長方形の面積は等しいね.
さらに,OとBで作られる長方形とOとCで作られる長方形の面積を比べれば,明らかにOとBが作られる長方形の面積が大きいね.
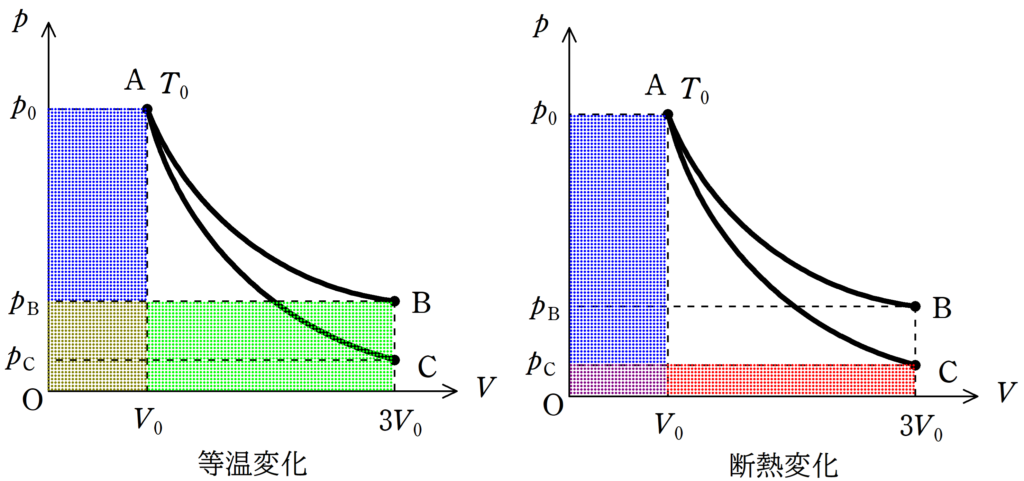
したがって,状態Bの方が温度が高い(答)
(2)

仕事の大小も$pV$図の曲線と$V$軸で囲まれた部分の面積をみればすぐにわかります.
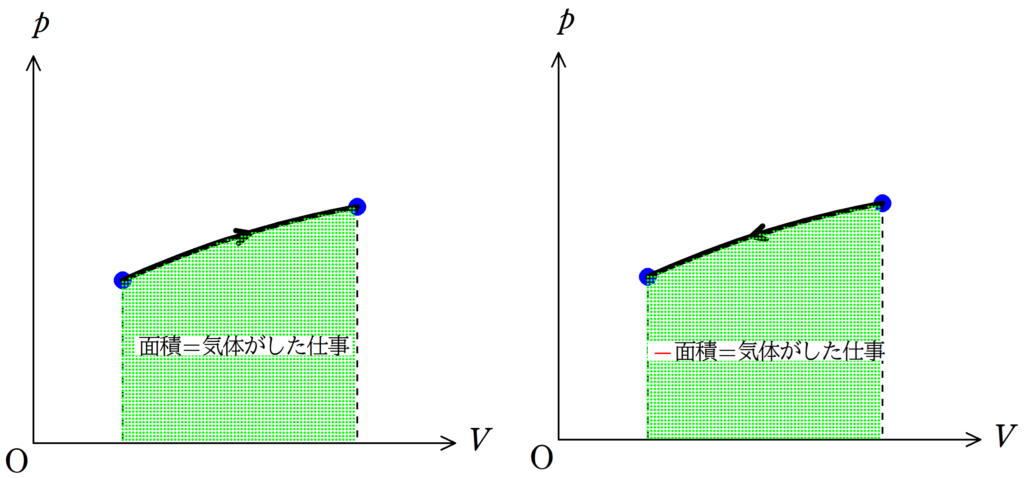
気体がした仕事は上図のように緑色部分の面積を求めることで計算ができる.
ただし,状態変化の矢印が右向きのときは
面積=気体がした仕事
であるが,状態変化の矢印が左向きのときは
-面積=気体がした仕事
である.
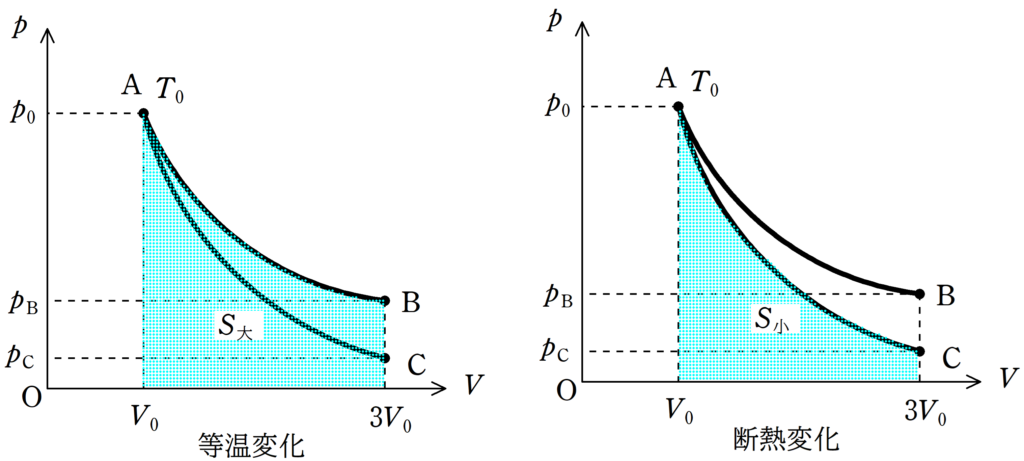

曲線ABと$V$軸で囲まれた面積と曲線ACと$V$軸で囲まれた面積を比べれば,曲線ABと$V$軸で囲まれた面積の方が大きいね.
したがって,$W_{\rm AB}$の方が大きい(答)
(3)
★ $p_{\rm B}$について
理想気体について,物質量$n$が変化しないとき,気体の圧力を$p$,気体の体積を$V$,絶対温度を$T$とすると,
$\dfrac{pV}{T}=$一定
が成り立つ.(ボイル・シャルルの法則)
特に,温度が一定のとき
$pV=$一定(ボイルの法則)
圧力が一定のとき
$\dfrac{V}{T}=$一定(シャルルの法則)
が成り立つ.
ボイルの法則より
$p_{\rm B}\cdot 3V_{0}=p_{0}V_{0}$ $\therefore$ $p_{\rm B}=\dfrac{1}{3}p_{0}$
★ $p_{\rm C}$について
準静的断熱変化をするとき,理想気体の圧力を$p$,体積を$V$,絶対温度を$T$,比熱比を$\gamma$とする.
ただし,$\gamma$は定積モル比熱$C_{\rm{V}}$と定圧モル比熱$C_{\rm{p}}$を用いて,$\gamma=\dfrac{C_{\rm{p}}}{C_{\rm{V}}}$.
このとき,以下のポアソンの式が成り立つ.
$pV^{\gamma}=$一定 ,$TV^{\gamma -1}=$一定
特に,単原子分子理想気体のとき,$C_{\rm{V}}=\dfrac{3}{2}R$,$C_{\rm{p}}=\dfrac{5}{2}R$より,$\gamma=\dfrac{5}{3}$となる.
ポアソンの式より
$p_{\rm B}\cdot (3V_{0})^{\frac{5}{3}}=p_{0}V_{0}^{\frac{5}{3}}$
$p_{\rm B}=3^{-\frac{5}{3}}p_{0}$


コメント
[…] […]
[…] […]