
前回の内容はこちらです.
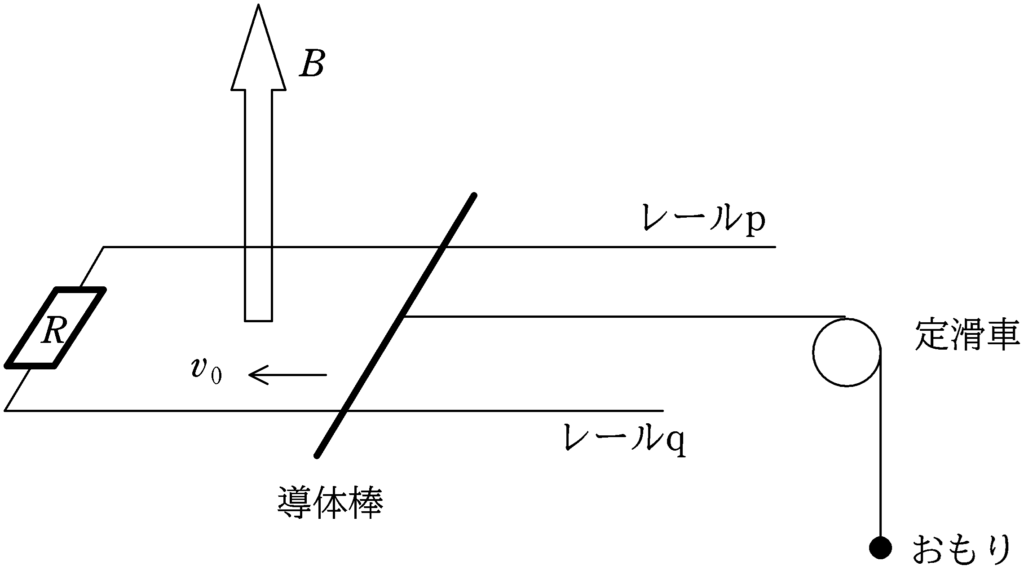
図のように水平面に平行な面に導体レールp , qが距離$l$を隔てて平行に固定されている.レールp , qに垂直に質量$m$の導体棒を置き,レールp , qを抵抗値$R$の抵抗で接続した.また,導体棒には軽くて伸びない糸がつながれており,この糸の他端には軽い滑車をとおして,質量$2m$のおもりにつながれている.おもりは鉛直方向に動くことができるようになっている.定滑車の摩擦,導体棒とレールの摩擦,抵抗値$R$の抵抗は無視をし,この回路の自己インダクタンスも無視をする.
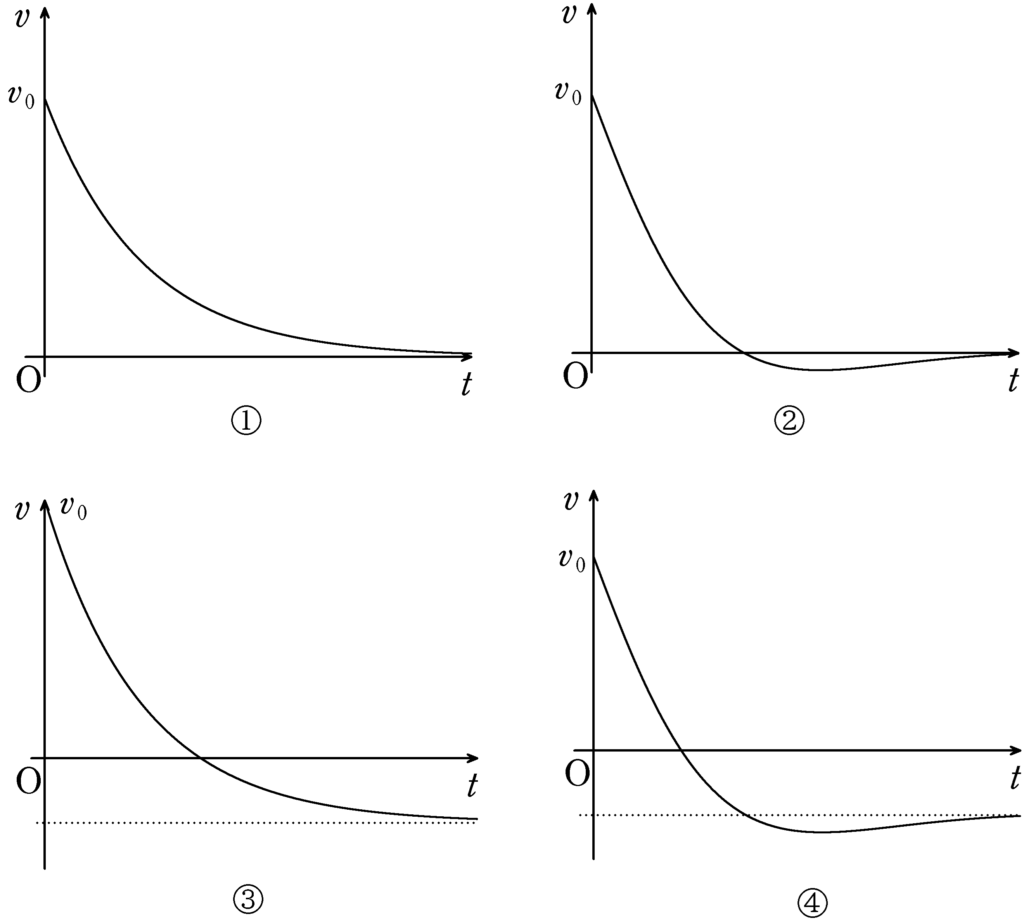
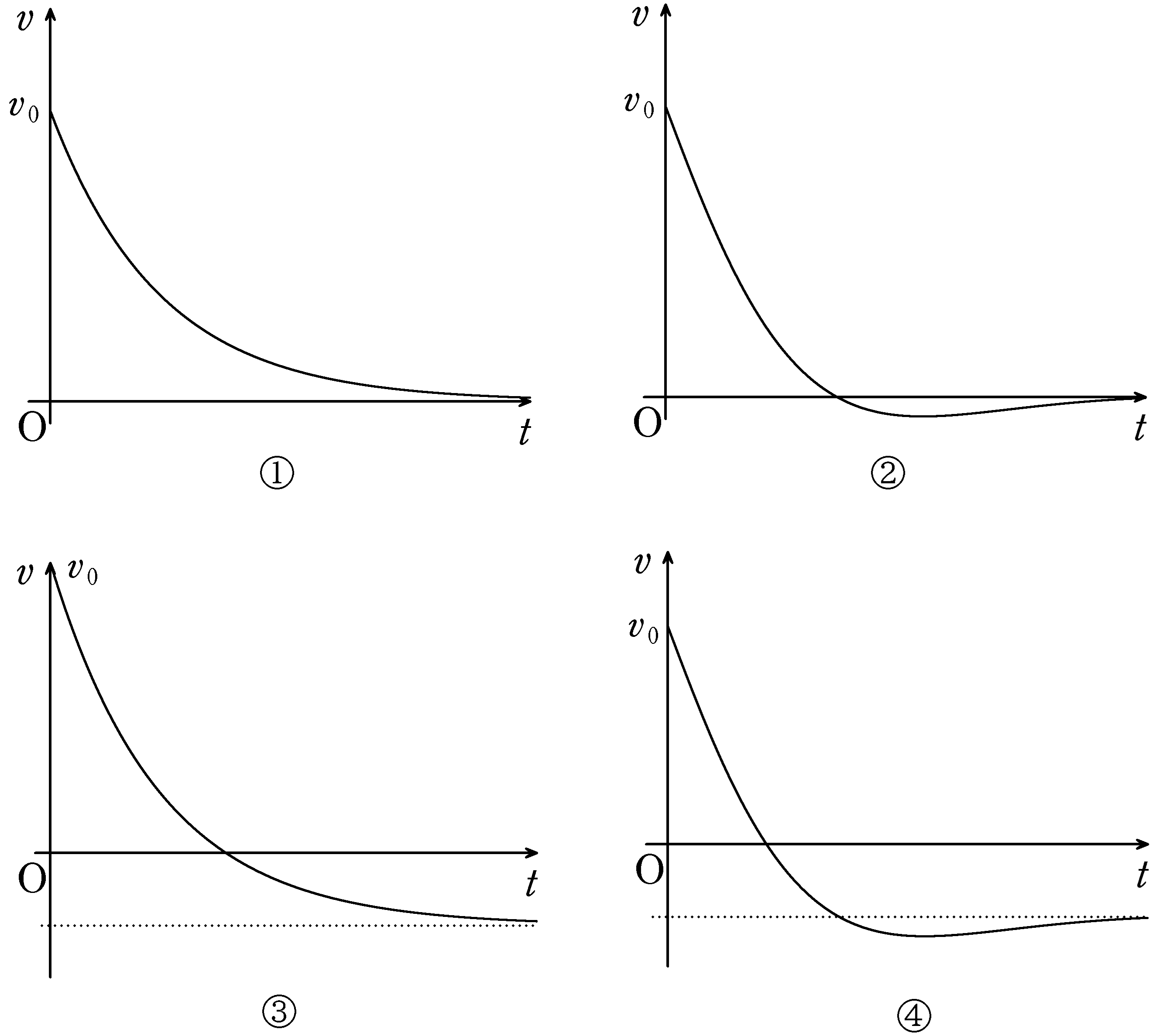
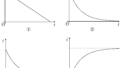
上図のように,鉛直上向きに磁束密度$B$の一様な磁場をかけ,時刻0で導体棒およびおもりに初速を与えた.初速度の向きはおもりが鉛直上向きに運動する方向で大きさは$v_{0}$である.初速度を与えた直後で糸は張ったままであるとする.このとき,おもりの速度の時間変化として最も適当なものを次の中から選べ.ただし,重力加速度の大きさを$g$とする.また,おもりの鉛直上向きの速度を正とする.

グラフの問題は「感覚的に選ぶ」のではなく,「式を立てて考察する」癖をつけましょう.
確認すべきことは,今までの導体棒の問題と一緒です.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式
★ キルヒホッフ則
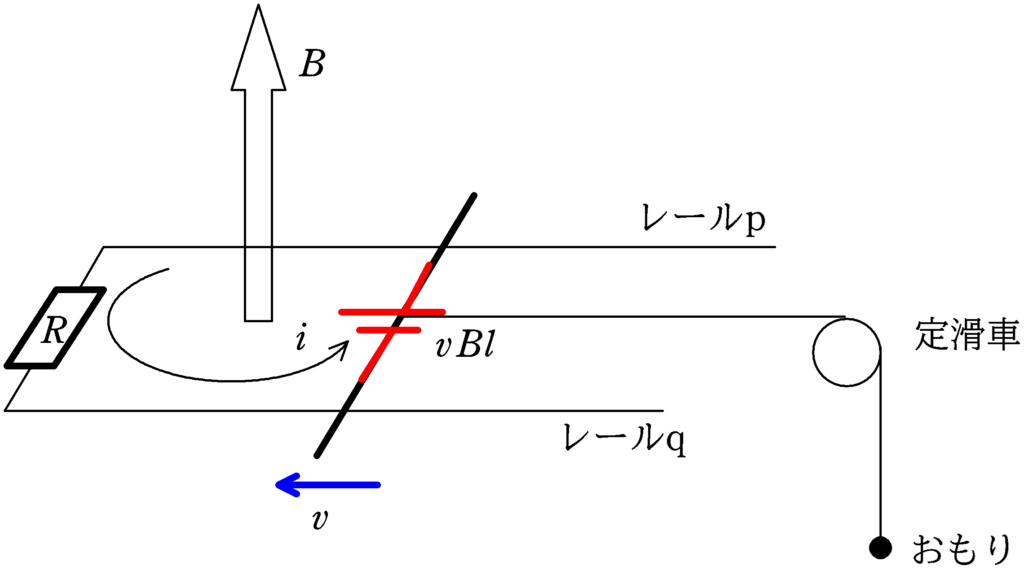
導体棒が速度$v$(問題設定通り,導体棒が左方向に移動する方向を正とする.)で動いているときの起電力は$vBl$となる.(※もし,$v<0$であれば,起電力の向きが逆になる.)図のように,鉛直上から見たときに反時計回りに電流$i$が流れるとする.このとき,キルヒホッフ則は
$vBl-Ri=0$
$i=\dfrac{vBl}{R}$ $\cdots (\ast)$
(※もし$v<0$なら,$i<0$となり,電流が時計回りに流れることに対応する.つまり,わざわざ$v$の正負で場合分けをしなくてもよい.)
★ 運動方程式
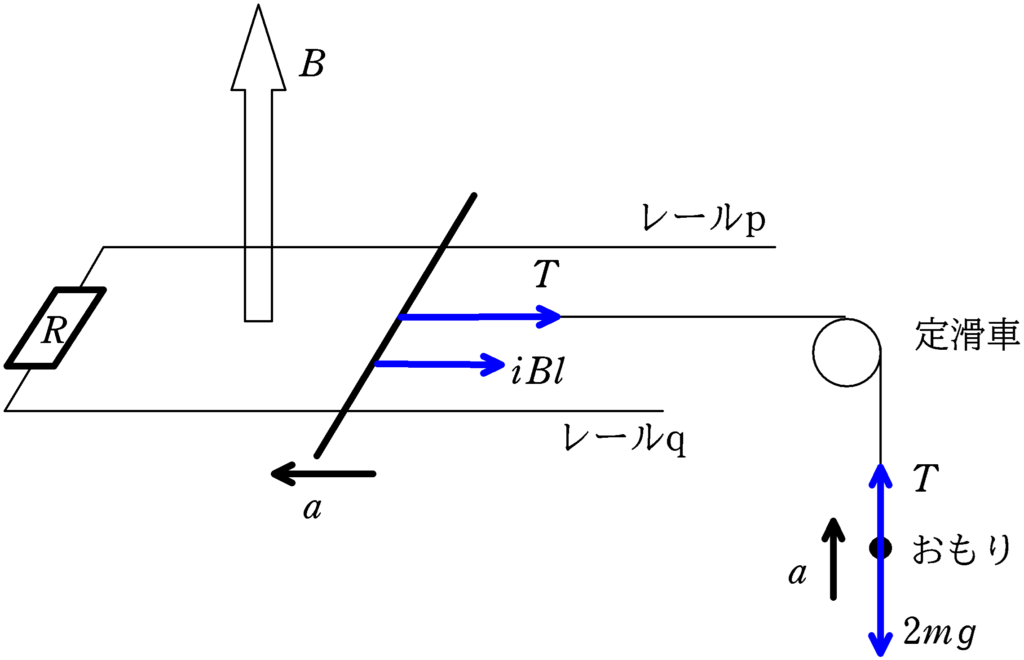
速度$v$のときの導体棒およびおもりの加速度を$a$とする.張力の大きさを$T$として,導体棒およびおもりの運動方程式を立てると
$ma=-iBl-T$
$2ma=T-2mg$
2式を足して,$T$を消去すると
$3ma=-iBl-2mg$ $\cdots (2\ast)$
$(\ast)$を$(2\ast)$に代入して,$i$を消去すると
$3ma=-\dfrac{B^{2}l^{2}}{R}v-2mg$ $\cdots (\sharp)$

今回も終端速度型の運動方程式になったね.
ということは,$t=0$での$a\,(vtグラフの傾き)$を調べるのと,$t\to \infty$で$a$(傾き)が$0$という性質からグラフを選べばいいね.
質量を$m$,加速度を$a$,速度を$v$,$C$を定数とすると
$ma=-kv+C$
は終端速度型の運動方程式である.
終端速度型の運動方程式は次の特徴がある.
十分時間が経つと,速度が一定(加速度が0)になる.
速度が一定になったときの速度を終端速度という.
終端速度は運動方程式に$a=0$を代入して
$0=-kv+C$ $\therefore v=\dfrac{C}{k}$
また,$t=0$のときの速度を$v_{0}$とすると,そのときの加速度($v-t$グラフの傾き)は
$a=\dfrac{-kv_{0}+C}{m}$
となる.

$(\sharp)$の式に$t=0$のときの速度$v_{0}$を代入すると,$t=0$のときの$v-t$グラフの傾き(加速度$a_{0}$)がわかります.
$3ma_{0}= -\dfrac{B^{2}l^{2}}{R}v_{0}-2mg $
$\therefore a_{0}=-\dfrac{B^{2}l^{2}}{3mR}v_{0}-\dfrac{2}{3}g\,(<0)$
結果は複雑だけど,傾きが負であることがわかったね.
速度が小さくなっていくと,傾きの絶対値がだんだんと小さくなります.
そして,十分時間が経つと,傾きが$0$(加速度が$0$)になって,速度が変化しなくなります.このときの速度$v_{\infty}$は$(\sharp)$より
$0= -\dfrac{B^{2}l^{2}}{R}v_{\infty}-2mg $
$\therefore v_{\infty}=-\dfrac{2mgR}{B^{2}l^{2}}$
実は途中で,速度が$0$になって,導体棒とおもりは逆方向に動きます.速度が$0$になっても加速度は$-\dfrac{2}{3}g$($\sharp$に$v=0$を代入)なので,まだまだ速度変化がマイナスになるんだね.
ということで,次のようなグラフになります.
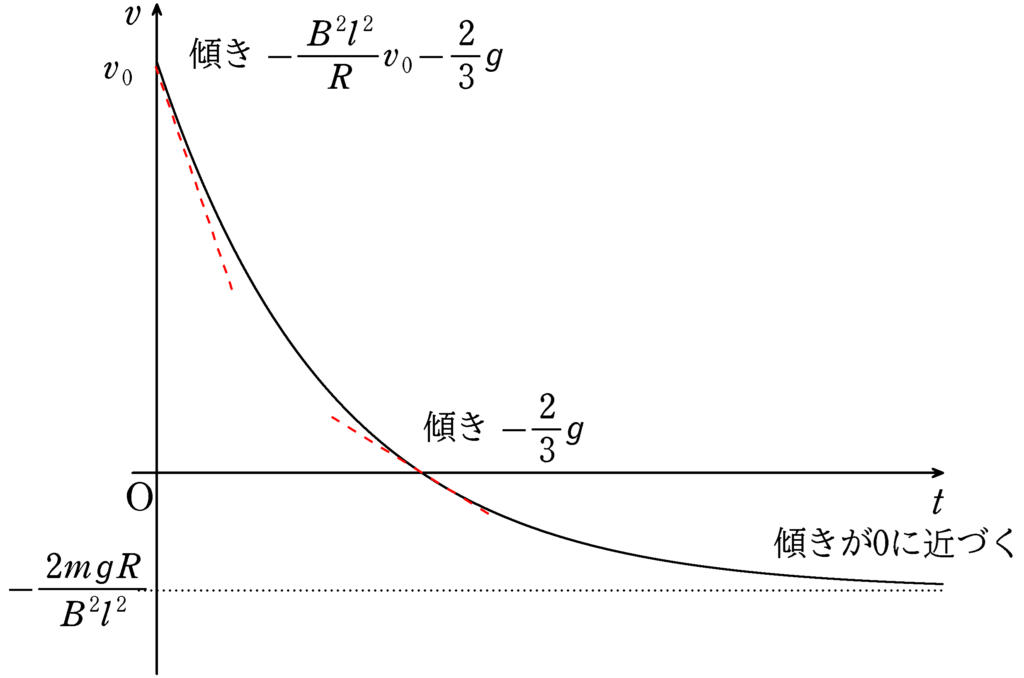
答えは③(答)

コメント
[…] 導体棒のグラフ対策3PHYさん前回の内容はこちらです.問題図のように水平… 問題 […]