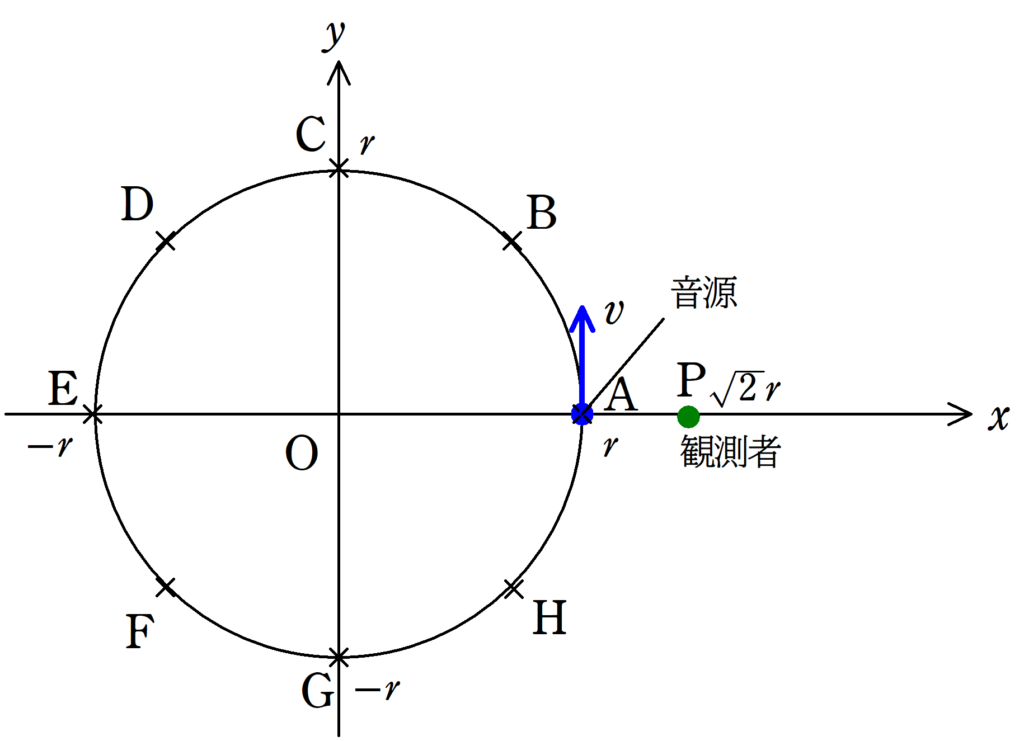
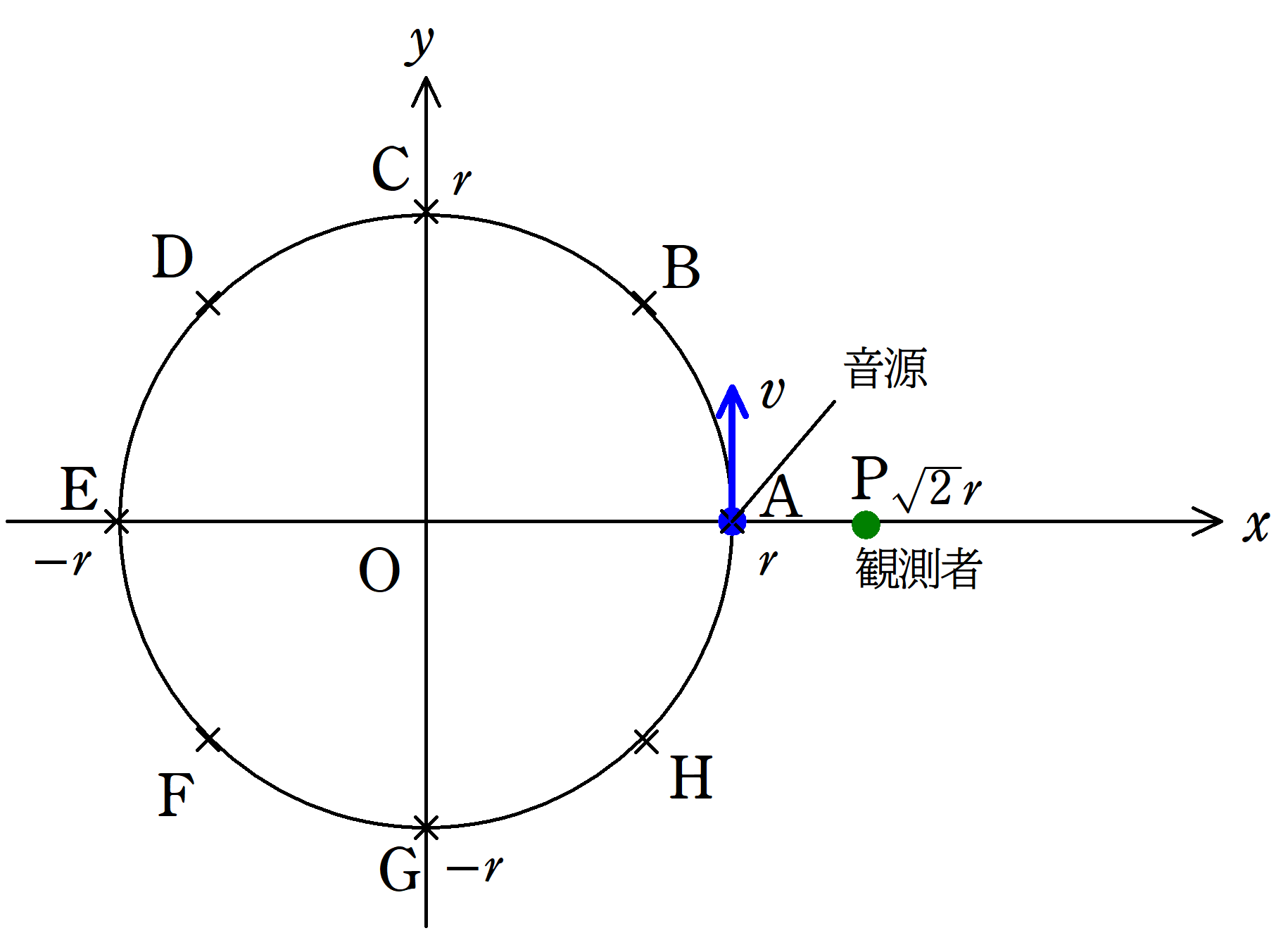
原点を中心とした半径$r$の円上を音源が速さ$v$で反時計回りに等速円運動している.
上図の座標${\rm P}(\sqrt{2}r , 0)$で観測者が静止して音を聞いている.
音源は$f_{0}$の振動数で音を出している.音の速さを$c$とするとき,次の問いに答えよ.
(1) ある時刻において,観測者が観測する振動数が最小値$f_{\rm min}$となった.$f_{\rm min}$となる音が出されたのは音源がA , B , C , D , E , F , G , Hのどの場所にいるときに出された音か.また,$f_{\rm min}$を求めよ.
(2) ある時刻において,観測者が観測する振動数が$f_{0}$であった.$f_{0}$と観測される音が出されたのは音源がA , B , C , D , E , F , G , Hのどの場所にいるときに出された音か.
(3) 観測者が最大の振動数を聞いてから,最小の振動数を聞くまでの時間を求めよ.
<解答>
(1)

救急車が近づくときは高い音が聞こえ,遠ざかるときには低く聞こえますね.
まずは,遠ざかる速度が一番大きい場所を探します.
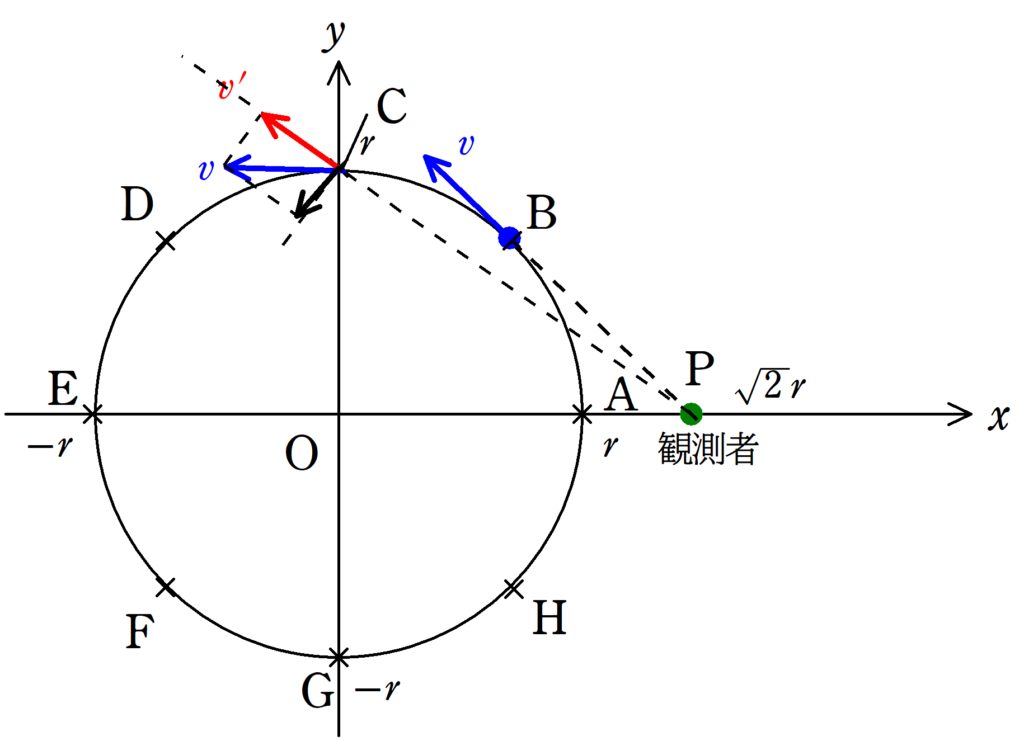
よくある間違いが$\rm C$です.
なんとなく,遠いし,遠ざかっているので$\rm C$が正解のような気がしますが,答えは$\rm B$です.
上図で確認してみましょう.$\rm C$は$\rm P$から遠ざかる成分は赤の速度成分$v^{\prime}$となるのですが,$\rm B$では分解せずとも$v$が遠ざかる成分となります.
BからPの方向へ向かう波長$\lambda_{\rm B}$は
$\lambda_{\rm B}=\dfrac{c+v}{f_{0}}$
となります.
したがって,求める振動数$f_{\rm min}$は
$\eqalign{f_{\rm min}&=\dfrac{c}{\lambda_{\rm B}}\\&=\dfrac{c}{\dfrac{c+v}{f_{0}}}\\&=\dfrac{c}{c+v}f_{0}}$ (答)
(2)
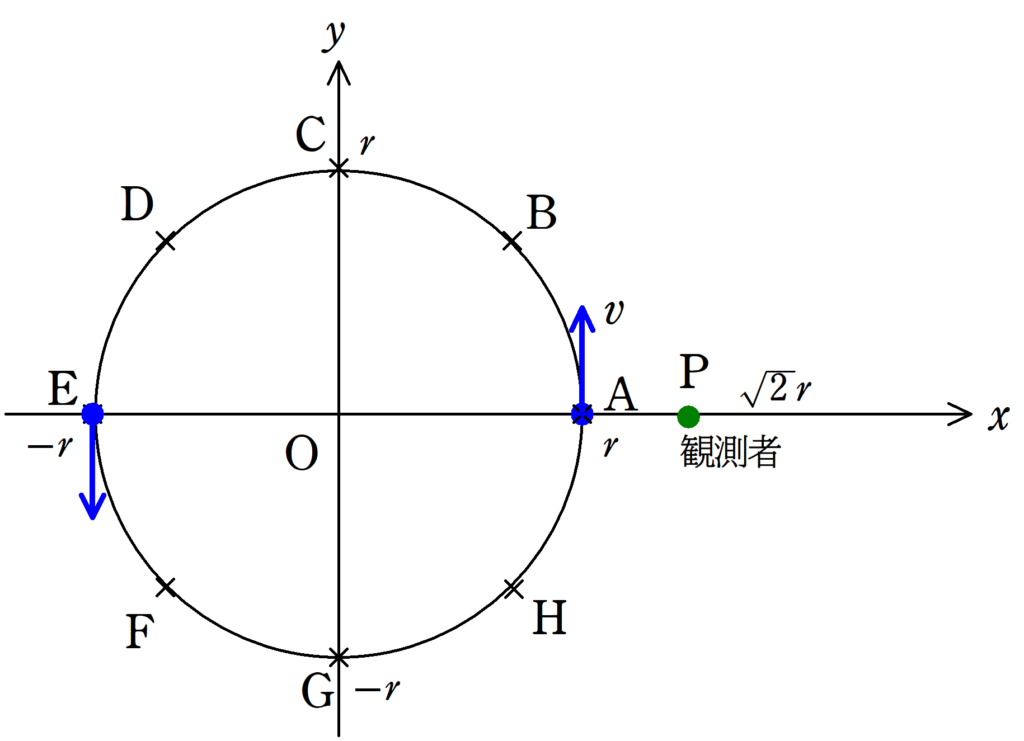

観測者が観測する振動数が$f_{0}$ということはドップラー効果が起こっていません.
つまり,観測者Pに近づきも遠ざかりもしないところを探せばよいですね.
その場所は$\rm A$と$\rm E$です.(答)
(3)
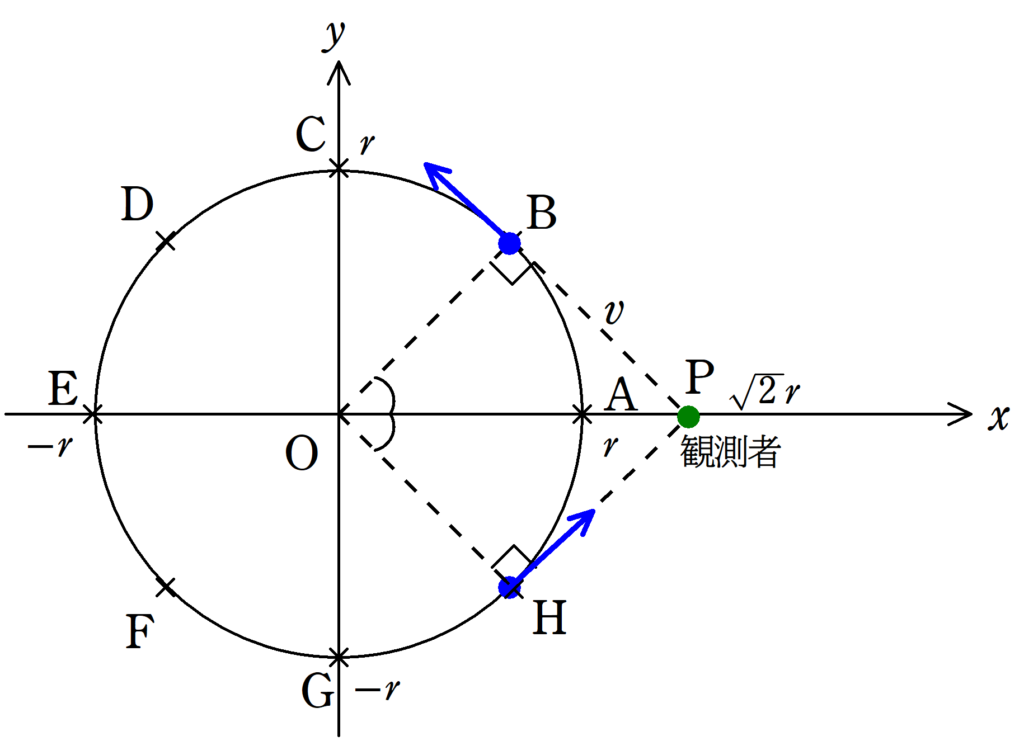

音源が$\rm B$にいるときに出された音が,観測者が聞こえる最小の振動数で,音源が$\rm H$にいるときに出された音が,観測が聞こえる最大の振動数となります.
そこで,$\triangle \rm OHP$と$\triangle \rm OBP$は直角二等辺三角形であることを利用しましょう.
すると,$\angle {\rm HOB}=90°$になるので,${\rm H\rightarrow A\rightarrow B}$と移動するのは周期$T$の$\dfrac{90°}{360°}=\dfrac{1}{4}$だけ時間がかかります.
円運動の周期は$T=\dfrac{2\pi r}{v}$なので
$\eqalign{\dfrac{1}{4}T&=\dfrac{1}{4}\cdot \dfrac{2\pi r}{v}\\&=\dfrac{\pi r}{2v}}$ (答)


コメント