
観測者と音源の運動が一直線上にない場合(いわゆる斜めのドップラー効果),速度を分解することで,一直線上のドップラー効果の問題にもっていきます.
速度を分解するときに,なぜかよくやってしまうミスについてもお話しします.

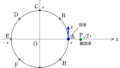
上図のように,地上に静止した観測者$\rm P$と一定の高さで地面と平行に速さ$v$で左がら右へ移動する音源がある.
音源が移動する直線を$l$とし,直線$l$上の十分遠い右方に点$\rm M$をとる.
ただし,音源は一定の振動数$f_{0}$の音を出し,音速を$c$とする.また,風は吹いていないものとする.
次の問いに答えよ.
(1) 音源が$\rm A$$(\angle {\rm MAP}=\theta_{1}(<90°))$にいるときに出した音を観測者が聞いたときの振動数$f_{1}$を求めよ.
(2) 音源が$\rm B$$(\angle {\rm MBP}=\theta_{2}(>90°))$にいるときに出した音を観測者が聞いたときの振動数$f_{2}$を求めよ.
<解答>
(1)

Aにいるときの音源の速度のうち,観測者に近づく成分を計算します.
速度を分解するときに下図のような間違いがよく見られるので注意してください.
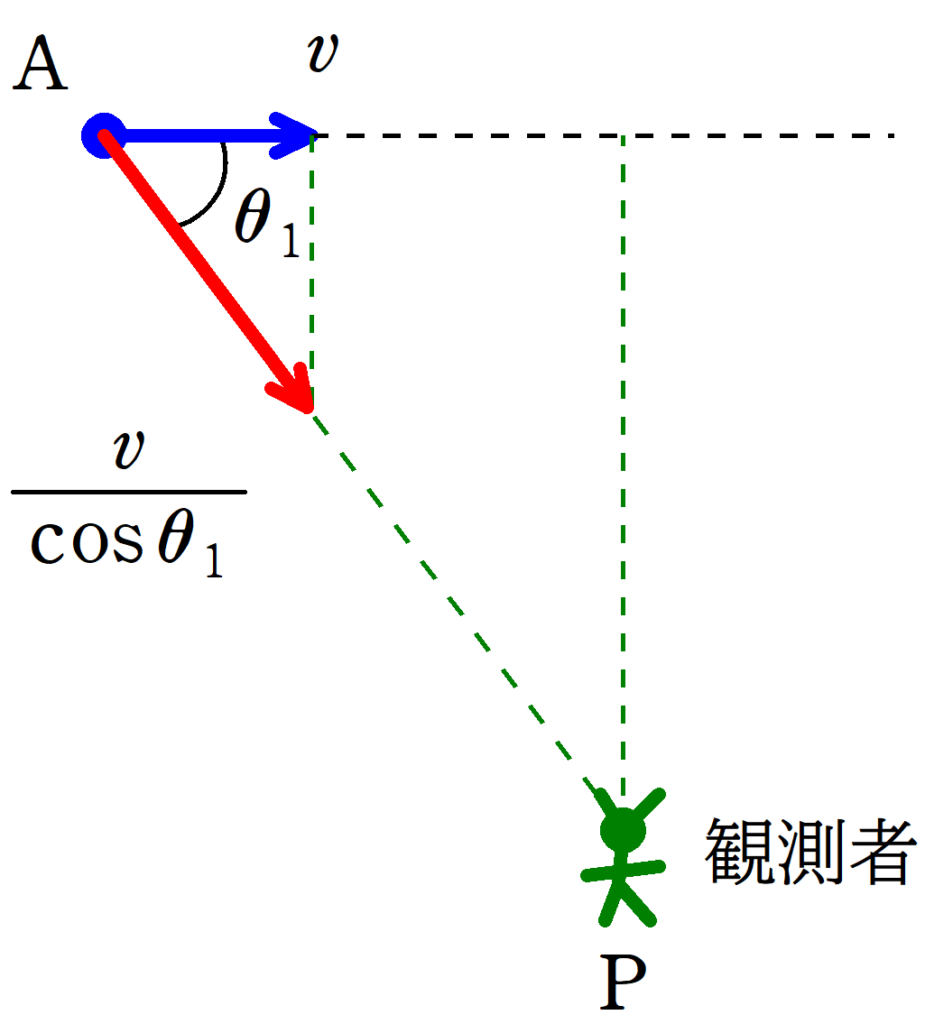

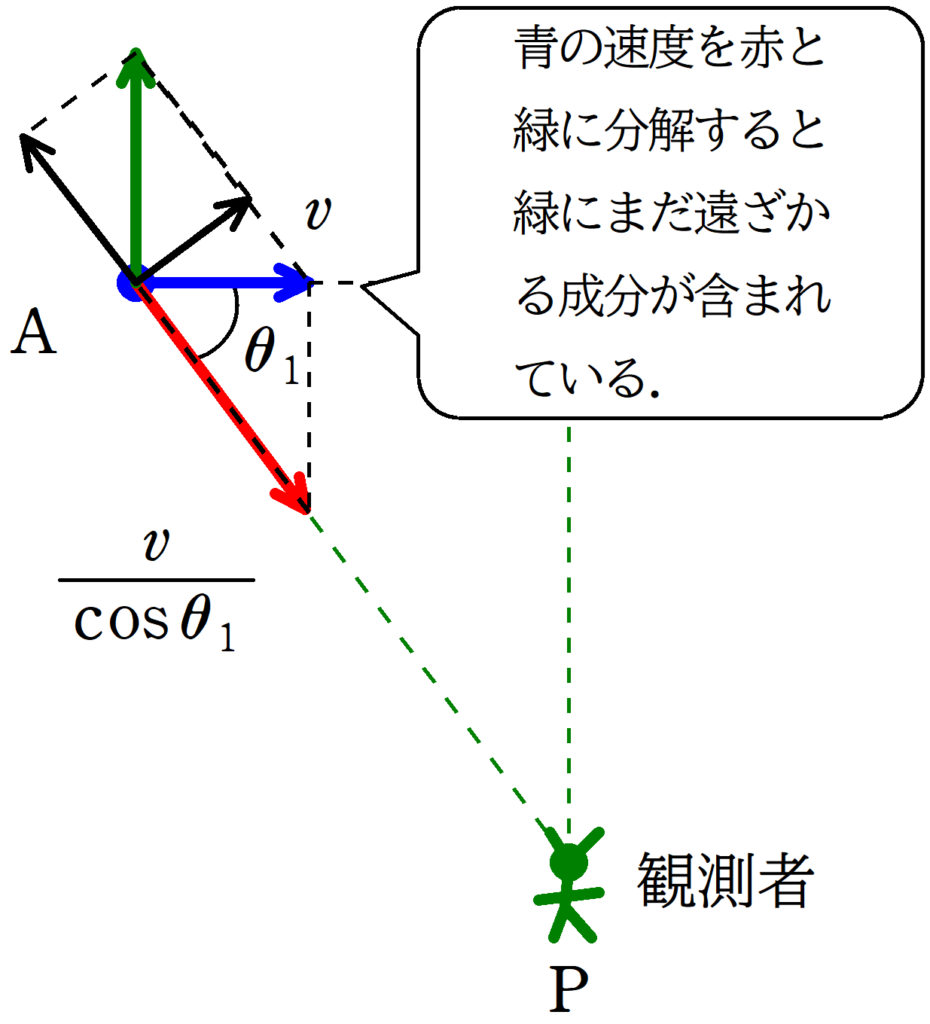
なぜ,上の速度の分解が間違いなのかは,下図で確認していきましょう.
青の速度を赤と緑の速度成分に分解すると,一見正しいような気がしますが,緑の速度成分は観測者から遠ざかる成分をもっています.(黒の矢印で観測者の方向に分解できる.)
なので,観測者に近づく速度成分は赤と緑を分解したうちの観測者に遠ざかる成分との和なのですが,いちいちこのようなことをやっていると面倒なので,
最初から別な形で速度を分解しましょう.

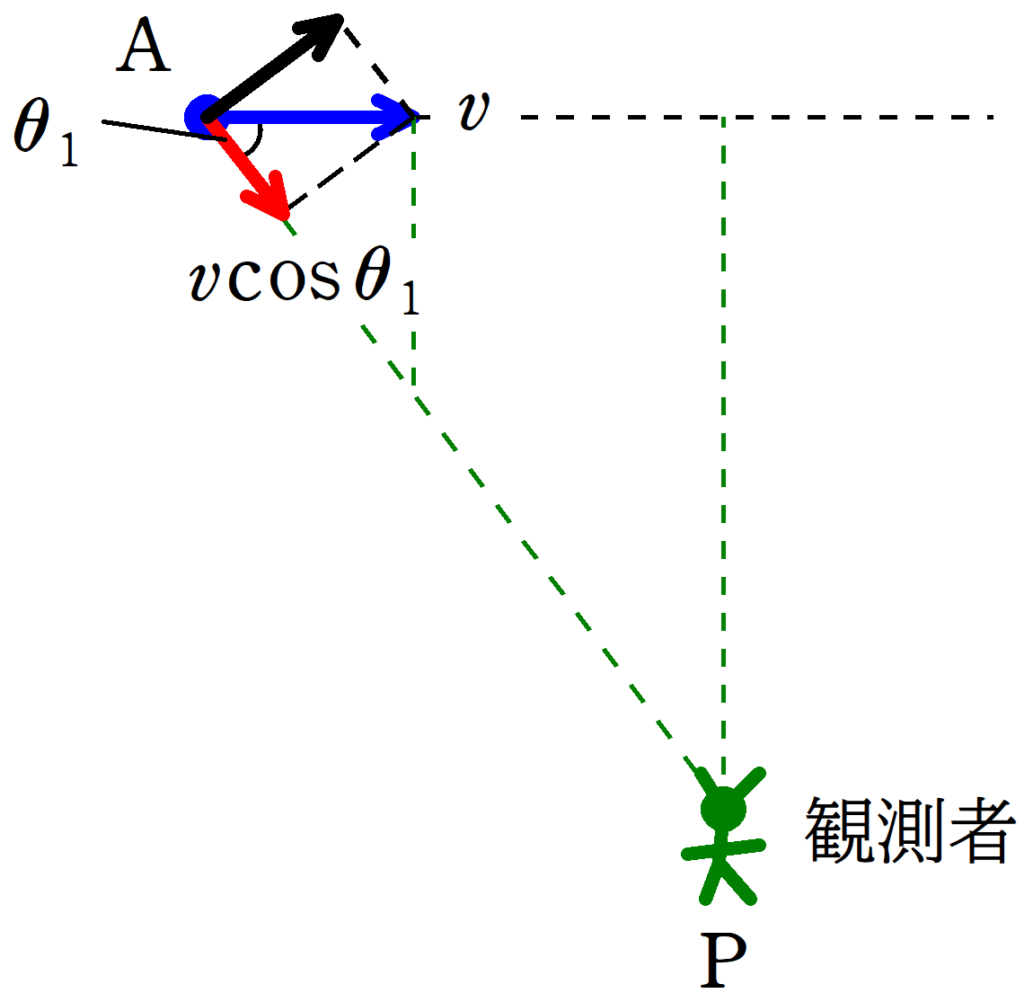
下図のように青の速度を赤の速度成分と黒の速度成分に分解すれば,黒の速度成分は観測者に近づいても遠ざかってもいないので大丈夫ですね.
赤の近づく成分は$v\cos \theta_{1}$です.
すると,観測者に向かう方向の波長$\lambda_{1}$は
$\lambda_{1}=\dfrac{c-v\cos\theta_{1}}{f_{0}}$
となるので,観測者が観測する振動数$f_{1}$は
$\eqalign{f_{1}&=\dfrac{c}{\lambda_{1}}\\&=\dfrac{c}{c-v\cos\theta_{1}}f_{0}}$ (答)
(2)

同じく$\rm B$にいるときについても速度を分解してみましょう.
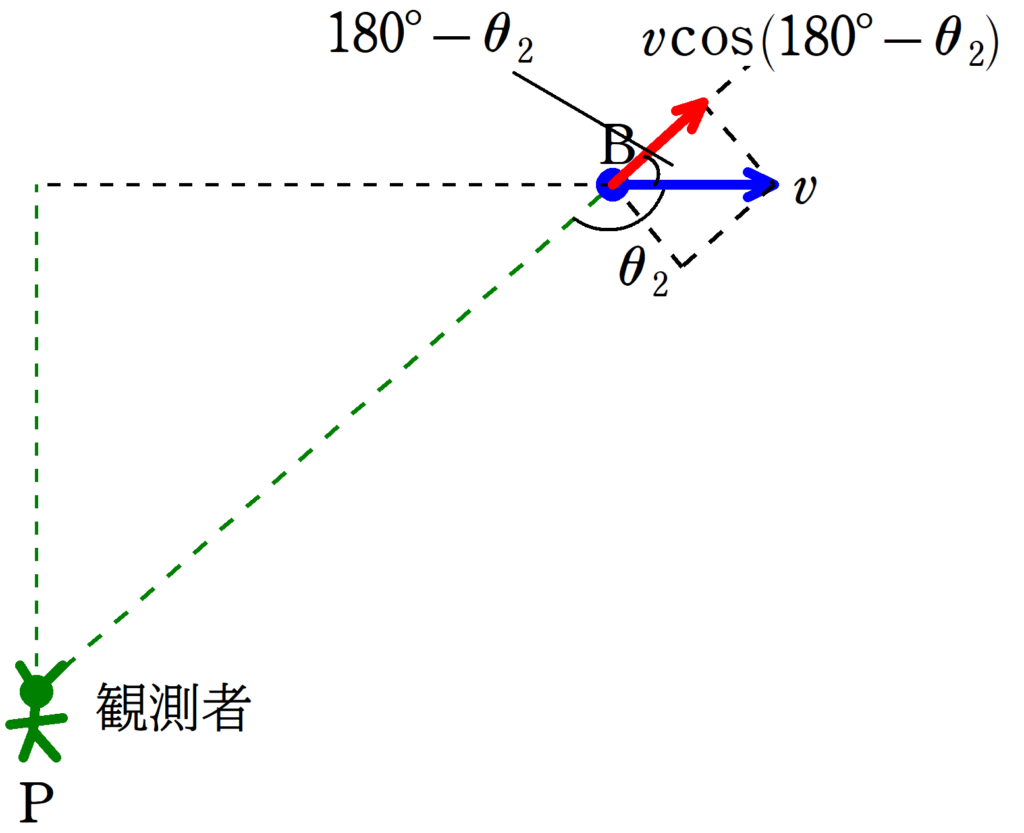

すると,観測者から遠ざかる速度成分は
$v\cos(180°-\theta_{2})=-v\cos\theta_{2}$
となります.
音源から出る観測者に向かう方向の波長$\lambda_{2}$は
$\eqalign{\lambda_{2}&=\dfrac{c+(-v\cos\theta_{2})}{f_{0}}\\&=\dfrac{c-v\cos\theta_{2}}{f_{0}}}$
したがって,観測者が観測する振動数$f_{2}$は
$\eqalign{f_{2}&=\dfrac{c}{\lambda_{2}}\\&=\dfrac{c}{c-v\cos\theta_{2}}f_{0}}$ (答)



コメント