
束縛条件の問題演習です.
他の問題はこちらにまとめられています.
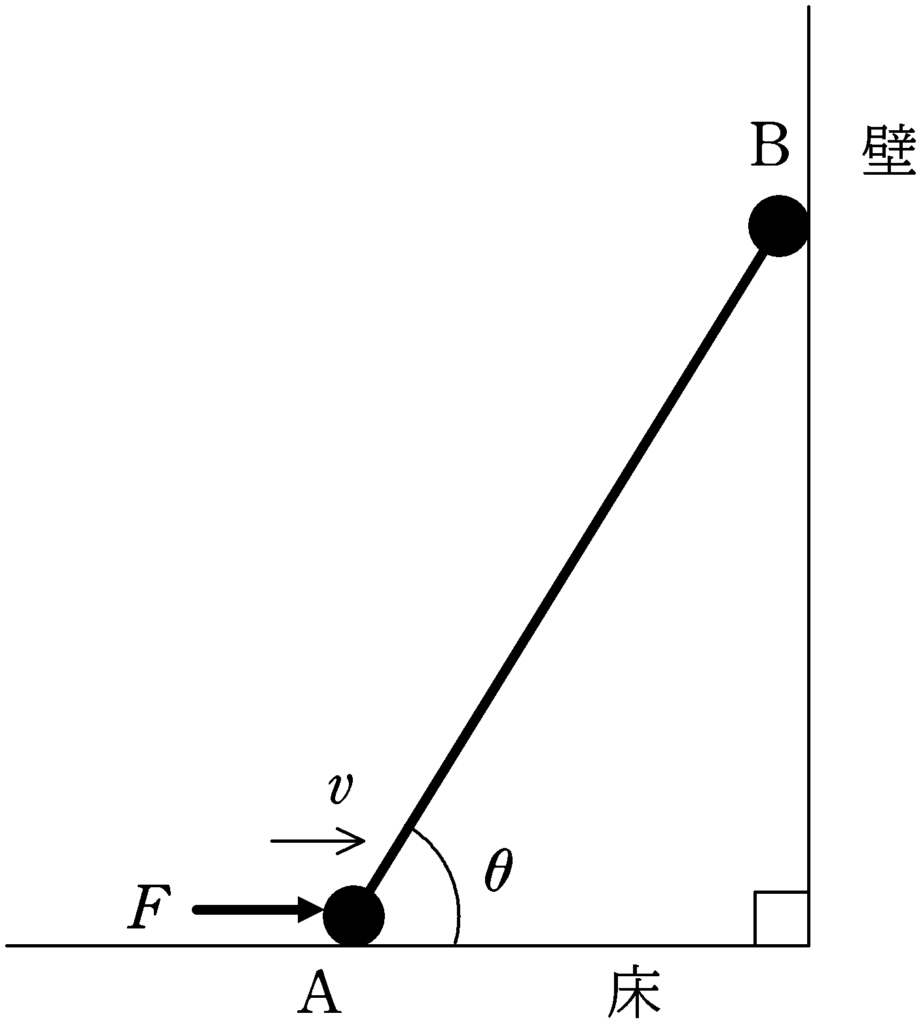
水平な床と床に対して垂直な壁がある.一方,長さ$l$の棒の両端に大きさが無視できる質量$m$の2つの小球A,Bをとりつける.小球Aは水平な床に接してあり,Bは壁に接している.Aに力を加え床に接したまま等速度$v$で壁に近づくようにする.このとき,Bは壁に接したままで鉛直方向に運動をした.棒と床とのなす角が$\theta$のときのBの鉛直方向の加速度$a_{y}$を求めたい.次の文章の(1)~(8)にあてはまる式を答えよ.ただし,棒と小球A,Bは同一鉛直面内を運動している.
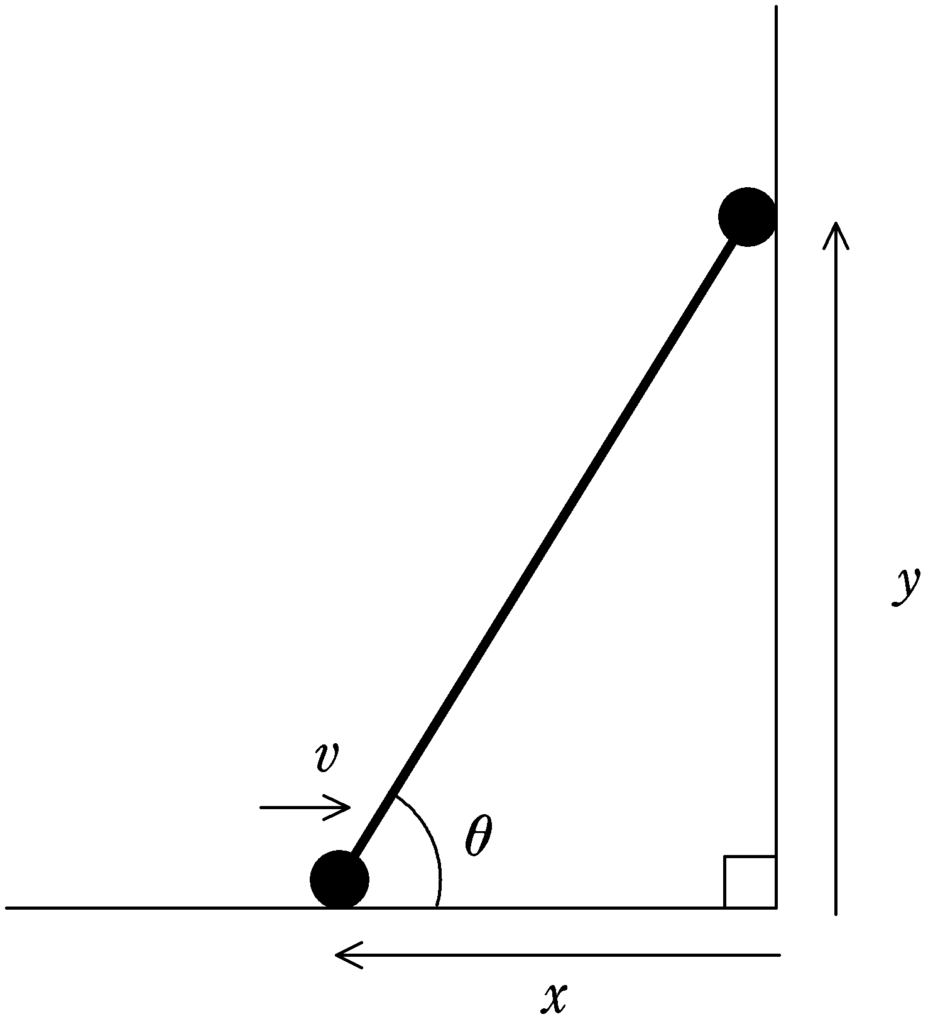
上図のように,床と壁の交点を原点として,水平左方向に$x$軸,鉛直上方向に$y$軸をとる.棒と床とのなす角が$\theta$のときのAの$x$座標を$x$,Bの$y$座標を$y$とする.このとき,三平方の定理より,$x,y,l$の関係式は(1)となる.また,非常に短い時間$\varDelta t$後のAの$x$座標は,$x$,$v$,$\varDelta t$を用いて(2)となり,Bの速度を$v_{y}$とすると,時間$\varDelta t$後の$y$座標は$y,v_{y},\varDelta t$を用いて(3)となる.(3)式において,$(\varDelta t)^{2}$の項は無視をし,(1)を用いると,$x,y,v,v_{y}$には関係式(4)が成立する.(4)式より,$v_{y}$を$v,\theta$を用いて表すと$v_{y}=$(5)が成りたつ.
また,非常に短い時間$\varDelta t$後のAの速度は$v$のままであるが,Bの速度は加速度を$a_{y}$とすると,$v_{y},\varDelta t$を用いて,(6)となる.このことから,(4)において,$\varDelta t$後の関係式を考えて,$a_{y},v,v_{y}$の間には(7)が成り立ち,$v,l,\theta$を用いて$a_{y}=$(8)を得る.
<解答>
(1) 三平方の定理より
$x^{2}+y^{2}=l^{2}$ (答)
(2) 小球Aは速さ$v$で壁に近づく方へ移動している.時間$\varDelta t$の間に$v\varDelta t$移動するので,Aの$x$座標は
$x-v\varDelta t$ (答)
(3) 時間$\varDelta t$後のBの$y$座標は
$y+v_{y}\varDelta t$ (答)
(4) 時間$\varDelta t$後について三平方の定理より
$\eqalign{(x-v\varDelta t)^{2}+(y+v_{y}\varDelta t)^{2}&=l^{2}\cr x^{2}-2xv\varDelta t+v^{2}(\varDelta t)^{2}+y^{2}+2yv_{y}\varDelta t+v_{y}^{2}(\varDelta t)^{2}&=l^{2}}$
$x^{2}+y^{2}=l^{2}$と,$(\varDelta t)^{2}$の項を無視して
$\eqalign{-2xv\cancel{\varDelta t}+2yv_{y}\cancel{\varDelta t}&=0 \cr -xv+yv_{y}&=0}$ (答)

ちなみにこの式は
$x^{2}+y^{2}=l^{2}$
の両辺を$t$で微分して
$2x\dfrac{dx}{dt}+2y\dfrac{dy}{dt}=0$
に,$\dfrac{dx}{dt}=-v$,$\dfrac{dy}{dt}=v_{y}$を代入して
$\eqalign{2x\times (-v)+2yv_{y}&=0\cr -xv+yv_{y}&=0}$
と同じ結果です.
(5) (4)式に,$x=l\cos\theta,y=l\sin\theta$を代入して
$\eqalign{-l\cos\theta\times v+l\sin\theta\times v_{y}&=0\cr \therefore v_{y}&=\dfrac{\cos\theta}{\sin\theta}v=\dfrac{v}{\tan\theta}}$ (答)
(6) 加速度の定義より,時間$\varDelta t$後のBの速度を$v_{y}’$として,
$\eqalign{a_{y}&=\dfrac{v_{y}’-v_{y}}{\varDelta t} \cr \therefore v_{y}’&=v_{y}+a_{y}\varDelta t}$ (答)
(7) 微小時間$\varDelta t$後の小球Aの$x$座標は,$x-v\varDelta t$,速度は$v$のまま.小球Bの座標は$y+v_{y}\varDelta t$,速度が(6)より,$v_{y}+a_{y}\varDelta t$である.
(5)で得た式$-xv+yv_{y}=0$において,$x\to x-v\varDelta t$,$v\to v$,$y\to y+v_{y}\varDelta t$,$v_{y}\to v_{y}+a_{y}\varDelta t$として,
$\eqalign{-(x-v\varDelta t)v+(y+v_{y}\varDelta t)(v_{y}+a_{y}\varDelta t)=0\cr -xv+v^{2}\varDelta t+yv_{y}+ya_{y}\varDelta t+v_{y}^{2}\varDelta t+v_{y}a_{y}(\varDelta t)^{2}&=0}$
(4)の式より,$-xv+yv_{y}=0$と,$(\varDelta t)^{2}$の項を無視して
$\eqalign{v^{2}\cancel{\varDelta t}+ya_{y}\cancel {\varDelta t}+v_{y}^{2}\cancel{\varDelta t}&=0\cr \therefore a_{y}&=-\dfrac{v^{2}+v_{y}^{2}}{y}}$
$y=l\sin\theta$,$v_{y}=\dfrac{v}{\tan\theta}$を代入して
$\eqalign{a_{y}&=-\dfrac{v^{2}+\dfrac{v^{2}}{\tan^{2}\theta}}{l\sin\theta}\\&=-\dfrac{\dfrac{\tan^{2}\theta +1}{\tan^{2}\theta}v^{2}}{l\sin\theta}}$
$\tan^{2}\theta+1=\dfrac{1}{\cos^{2}\theta}$であることと,$\dfrac{1}{\cos^{2}\theta \tan^{2}\theta}=\dfrac{1}{\sin^{2}\theta}$より,
$\eqalign{a_{y}&=-\dfrac{v^{2}}{l\sin^{3}\theta}}$ (答)

こちらも$-xv+yv_{y}=0$の両辺を$t$で微分することでも導出できます.$v$は定数であることと,積の微分より
$-\left(\dfrac{dx}{dt}\right)\times v+\dfrac{dy}{dt}v_{y}+y\dfrac{dv_{y}}{dt}=0$
$\dfrac{dx}{dt}=-v, a_{y}=\dfrac{dv_{y}}{dt}$より
$-(-v)\times v+v_{y}\times v_{y}+ya_{y}=0$
$\therefore a_{y}=-\dfrac{v^{2}+v_{y}^{2}}{l\sin\theta}$
となります.


コメント