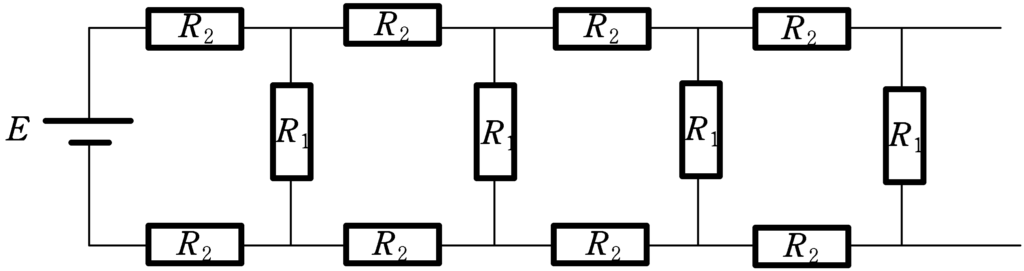
図のように,抵抗値$R_{1}$,$R_{2}$の抵抗と内部抵抗が無視できる起電力$E$の直流電池を用いて,回路をつくった.図は途中までしかかかれていないが,図の右側部分には同じ構造のものが十分多く接続されている.$R_{1}=4r,R_{2}=r$のとき,直流電池に流れる電流の大きさを求めよ.
<解答>
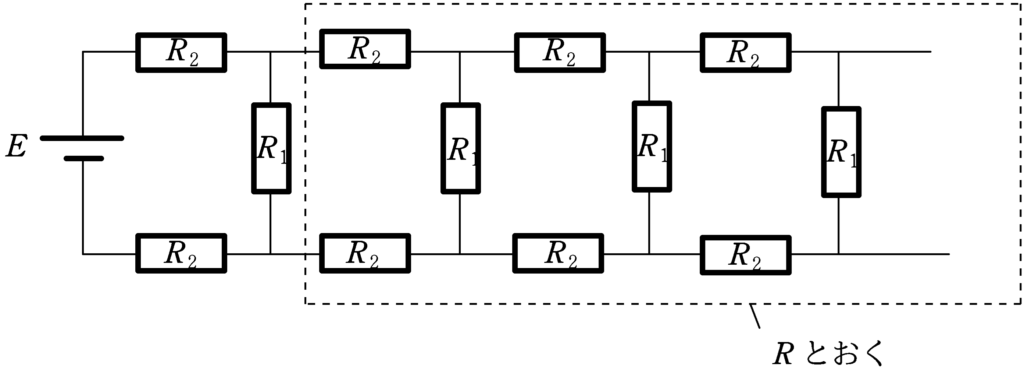

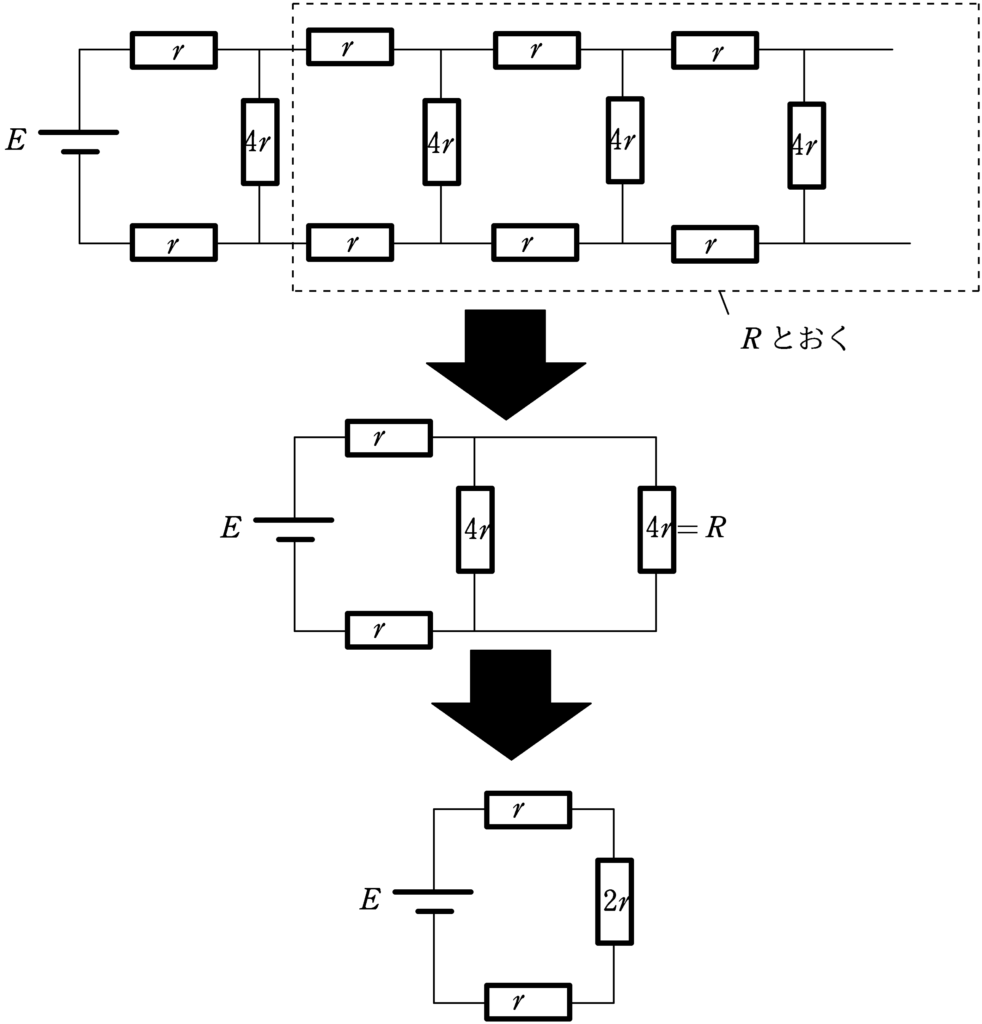
とりあえず,繰り返し続く部分の合成抵抗を$R$とおいてみます.
今度はこの$R$の部分に着目しましょう.
$R_{1}=4r,R_{2}=r$として回路は,次のようになります.
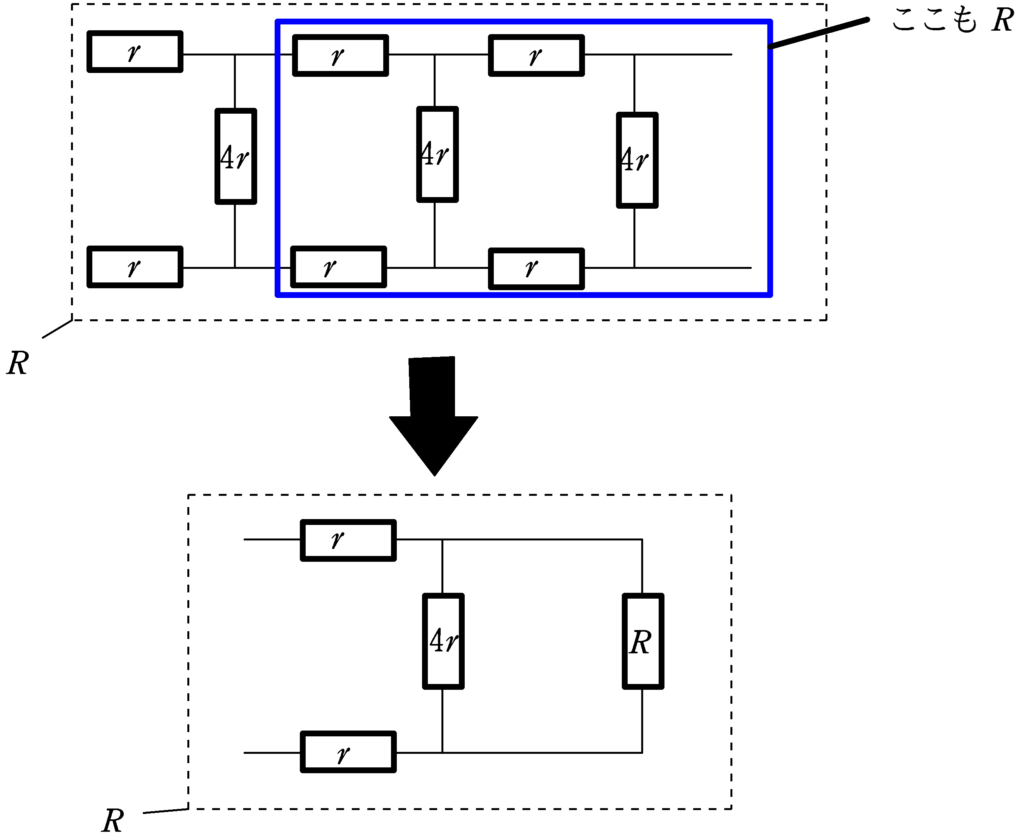

回路がほぼ無限に続くので,上図の青色四角で囲まれた部分も$R$とみなしてよいでしょう.
$4r$と$R$は並列合成をしましょう.並列合成は,逆数の和を計算したものをさらに逆数をとると導出できます.
$\eqalign{\left(\dfrac{1}{4r}+\dfrac{1}{R}\right)^{-1}&=\left(\dfrac{4r+R}{4Rr}\right)^{-1}\\&=\dfrac{4Rr}{4r+R}}$
この計算より,抵抗$R$は下図のように,$r$と$\dfrac{4Rr}{4r+R}$と$r$を直列に接続したものであることがわかります.直列合成は,単純に抵抗の足し算をすれば導出できます.
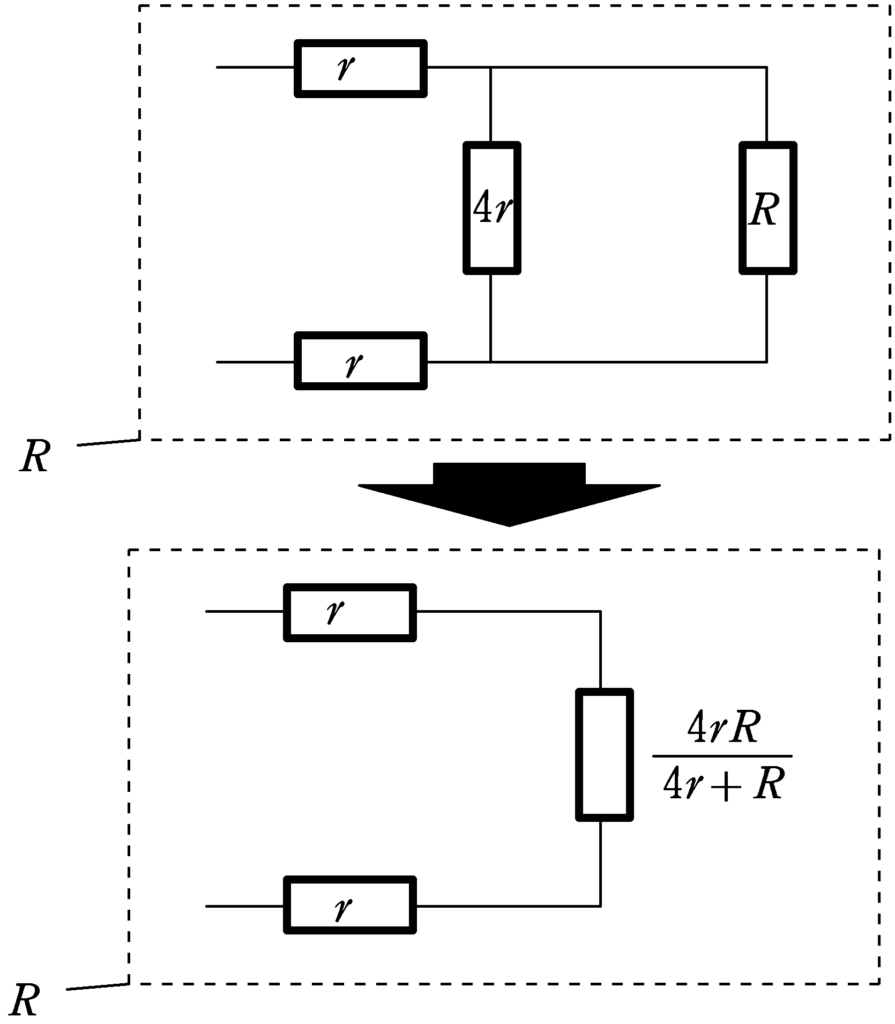
$\eqalign{R&=r+\dfrac{4Rr}{4r+R}+r\\&=2r+\dfrac{4Rr}{4r+R}}$
両辺$4r+R$をかけて整理する.
$\eqalign{R(4r+R)&=2r(4r+R)+4Rr\cr \cancel{4Rr}+R^{2}&=8r^{2}+2Rr+\cancel{4Rr}\cr R^{2}-2rR-8r^{2}&=0\cr (R-4r)(R+2r)&=0}$

$R=4r$または$-r$となりますが,$R>0$より,$R=4r$であることがわかります.
したがって,複雑であった回路は次のようになります!
途中,$4r$と$4r$の並列合成もしています.
$\eqalign{\left(\dfrac{1}{4r}+\dfrac{1}{4r}\right)^{-1}&=\left(\dfrac{1}{2r}\right)^{-1}\\&=2r}$
です.
直流電池に流れる電流を$i_{1}$とすると,キルヒホッフの法則より
$E-ri_{1}-2ri_{1}-ri_{1}=0$
$i_{1}=\dfrac{E}{4r}$ (答)




コメント