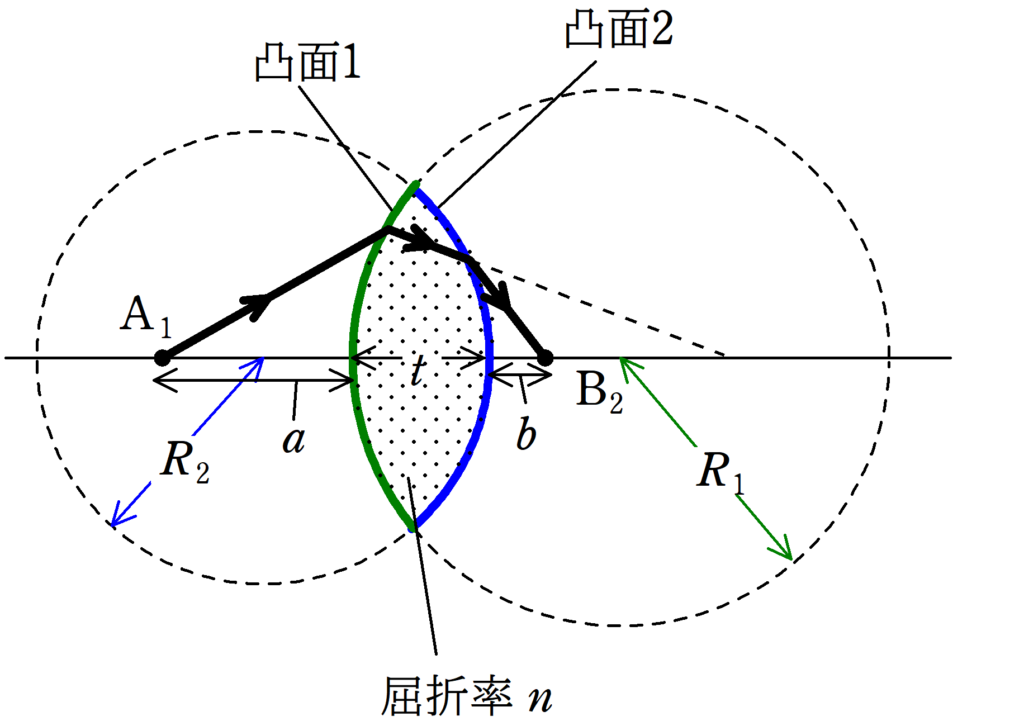
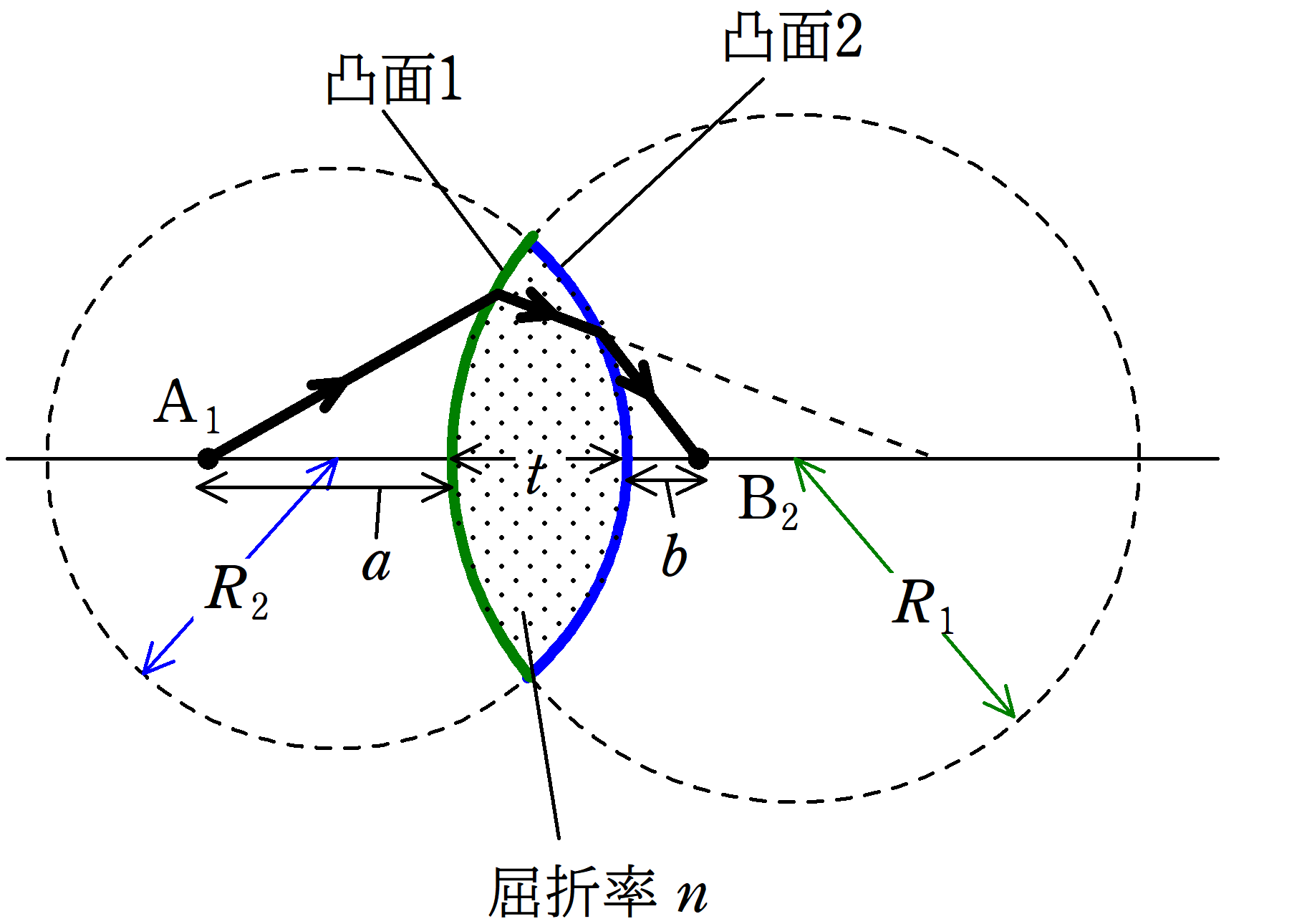
屈折率$n$からできている凸レンズについて考える.
凸レンズの左側部分である凸面1(緑の部分)は曲率半径$R_{1}$の球の一部であり,凸レンズの右側部分である凸面2(青の部分)は曲率半径$R_{2}$の球の一部である.
凸面1の中心と凸面2の中心を結ぶ光軸上の$\rm A_{1}$から出た光が凸面1,凸面2で屈折し,再び光軸上の点$\rm B_{2}$に到達する.
$\rm A_{1}$と凸面1との距離が$a$,凸面2と$\rm B_{2}$の距離が$b$である.
このとき,$a , b , n , R_{1} , R_{2}$の関係を導きたい.
次の文章の空欄に適切な数式を入れよ.
また,以下で角度$\delta$が非常に小さいとき,$\sin\delta\fallingdotseq \tan\delta \fallingdotseq\delta$を用いてよい.
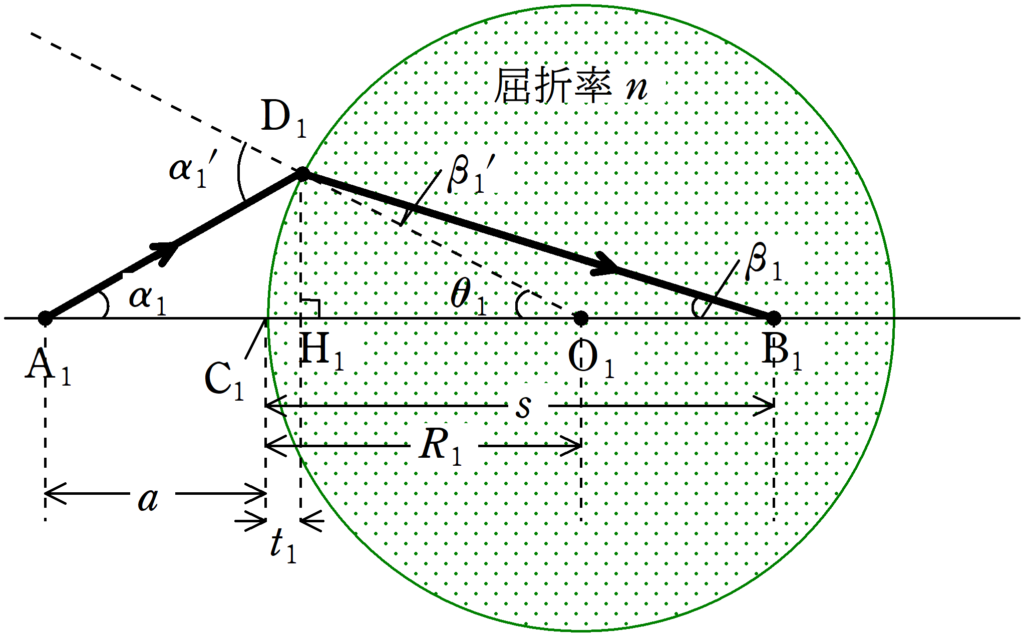
屈折率1の空気中にある$\rm A_{1}$から光が出て,曲率半径$R_{1}$の凸面1上の点$\rm D_{1}$において屈折し,光軸上の$\rm B_{1}$に到達した.凸面1の中心を$\rm O_{1}$,光軸と凸面1の$\rm A_{1}$に近い方の交点を$\rm C_{1}$,$\rm D_{1}$から光軸に下した垂線の足を$\rm H_{1}$とする.
${\rm C_{1}H_{1}}=t_{1}$,${\rm C_{1}B_{1}}=s$,$\angle{\rm D_{1}A_{1}H_{
1}}=\alpha_{1}$,$\angle{\rm D_{1}O_{1}H_{1}}=\theta_{1}$,$\angle{\rm D_{1}B_{1}H_{1}}=\beta_{1}$,$\rm D_{1}$に入射した光の入射角を$\alpha_{1}^{\prime}$,屈折角を$\beta_{1}^{\prime}$とする.
このとき,屈折の法則より,
$\sin\alpha_{1}^{\prime}=n\sin\beta_{1}^{\prime}$
が成り立つので,$\alpha_{1}^{\prime}$,$\beta_{1}^{\prime}$が小さいとして,$\alpha_{1}^{\prime}$,$\beta_{1}^{\prime}$,$n$の関係式は(1)となる.
また,$\triangle{\rm D_{1}A_{1}O_{1}}$の内角と外角の関係から$\alpha_{1}^{\prime}$,$\alpha_{1}$,$\theta_{1}$の関係式は(2)である.
また,$\triangle{\rm D_{1}O_{1}B_{1}}$の三角形の内角と外角の関係も考えて,$\beta_{1}$,$\beta_{1}^{\prime}$,$\theta_{1}$の関係は(3)である.
(1),(2),(3)より,$\alpha_{1}$,$\beta_{1}$,$\theta_{1}$,$n$の関係は(4)となる.
一方,$\triangle\rm D_{1}A_{1}H_{1}$より
$\tan\alpha_{1}=\dfrac{\rm D_{1}H_{1}}{a+t_{1}}$
さらに,$t_{1}\fallingdotseq 0$とすれば
$\tan\alpha_{1}\fallingdotseq\dfrac{\rm D_{1}H_{1}}{a}$
$\alpha_{1}$が小さいとき,$\alpha_{1}\fallingdotseq$(5)となる.
同様にして,$\beta_{1}$,$\theta_{1}$それぞれを$R_{1}$,$s$,$\rm D_{1}H_{1}$から必要なものを用いて表すと,$\beta_{1}\fallingdotseq$(6),$\theta_{1}\fallingdotseq$(7)となる.(5),(6),(7)を(4)に代入すると,$a$,$R_{1}$,$s$,$n$の関係式は(8)となる.
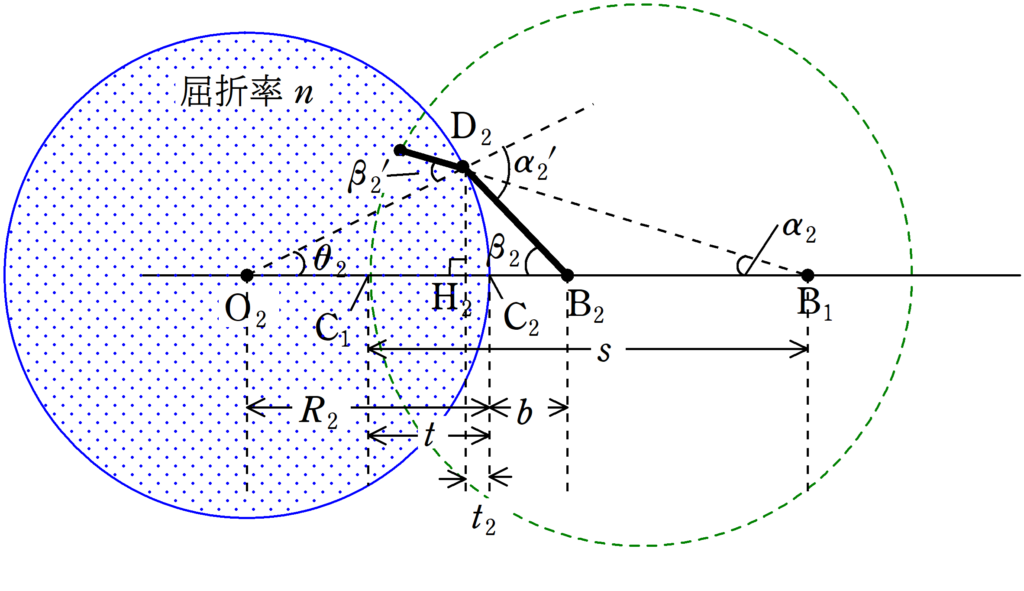
次に凸面2で屈折するときを考える.
凸面2の球の中心を$\rm O_{2}$,光線が凸面で屈折する点を$\rm D_{2}$,$\rm D_{2}$で屈折した光と光軸との交点を$\rm B_{2}$,入射光線と光軸との交点を$\rm B_{1}$,$\rm D_{2}$から光軸へ下した垂線の足を$\rm H_{2}$,凸面2と光軸の交点のうち,$\rm B_{2}$に近い方を$\rm C_{2}$とする.
${\rm C_{1}C_{2}}=t$,${\rm C_{2}H_{2}}=t_{2}$,${\rm C_{2}B_{2}}=b$,$\angle{\rm D_{2}O_{2}H_{2}}=\theta_{2}$,$\angle{\rm D_{2}B_{2}H_{2}}=\beta_{2}$,$\angle{\rm D_{2}B_{1}H_{2}}=\alpha_{2}$,$\rm D_{2}$のおける入射角を$\beta_{2}^{\prime}$,屈折角を$\alpha_{2}^{\prime}$とする.
このとき,$\rm D_{2}$における屈折の法則より
$n\sin\beta_{2}^{\prime}=\sin\alpha_{2}^{\prime}$
$\beta_{2}^{\prime}$,$\alpha_{2}^{\prime}$が十分小さいとき,$\beta_{2}^{\prime}$,$\alpha_{2}^{\prime}$の関係式は(9)となる.
$\triangle{\rm D_{2}O_{2}B_{2}}$について,内角と外角の関係より,$\alpha_{2}^{\prime}$,$\theta_{2}$,$\beta_{2}$の関係式は(10)となる.また,$\triangle{\rm D_{2}O_{2}B_{1}}$について,内角と外角の関係より,$\alpha_{2}$,$\beta_{2}^{\prime}$,$\theta_{2}$の関係式は(11)となる.
(9),(10),(11)より,$\alpha_{2}$,$\beta_{2}$,$\theta_{2}$,$n$の関係式は(12)となる.
一方,$\triangle{\rm D_{2}B_{1}H_{2}}$について
$\tan\alpha_{2}=\dfrac{\rm D_{2}H_{2}}{s-t+t_{2}}$
$t\fallingdotseq 0$,$t_{2}\fallingdotseq 0$とすれば,上式は
$\tan\alpha_{2}\fallingdotseq \dfrac{\rm D_{2}H_{2}}{s}$
さらに,$\alpha_{2}$が非常に小さいとして,$\alpha_{2}\fallingdotseq$(13)となる.
$\triangle{\rm D_{2}B_{2}H_{2}}$,$\triangle{\rm D_{2}O_{2}H_{2}}$についても同様に考える.$R_{2}$,$b$,$\rm D_{2}H_{2}$から必要なものを用いて,$\beta_{2}\fallingdotseq$(14),$\theta_{2}\fallingdotseq$(15)となる.
(13),(14),(15)を(12)に代入すると,$s$,$b$,$R_{2}$,$n$の関係式は(16)となる.
(8)と(16)より,$s$を消去すると,$a$,$b$,$n$,$R_{1}$,$R_{2}$の関係式は(17)である.
<解答>

問題の誘導に従って計算していけば解けるようになっています.
(1)
問題文で,「角度$\delta$が非常に小さいとき,$\sin\delta\fallingdotseq \tan\delta \fallingdotseq\delta$を用いてよい.」と書かれているので,この近似式を使っていきましょう.
$\sin\alpha_{1}^{\prime}=n\sin\beta_{1}^{\prime}$
において,$\sin\alpha_{1}^{\prime}\fallingdotseq \alpha_{1}^{\prime}$,$\sin\beta_{1}^{\prime}\fallingdotseq \beta_{1}^{\prime}$として
$\alpha_{1}^{\prime}=n\beta_{1}^{\prime}$ (答)
(2)
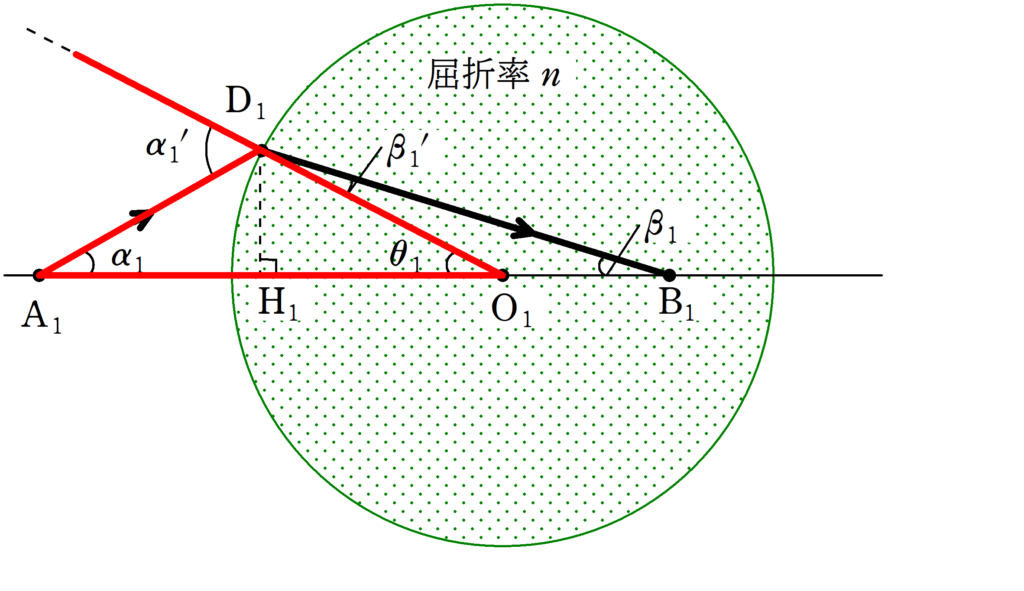
上図の赤色で囲まれた三角形の内角と外角の関係より
$\alpha_{1}^{\prime}=\alpha_{1}+\theta_{1}$ (答)
(3)
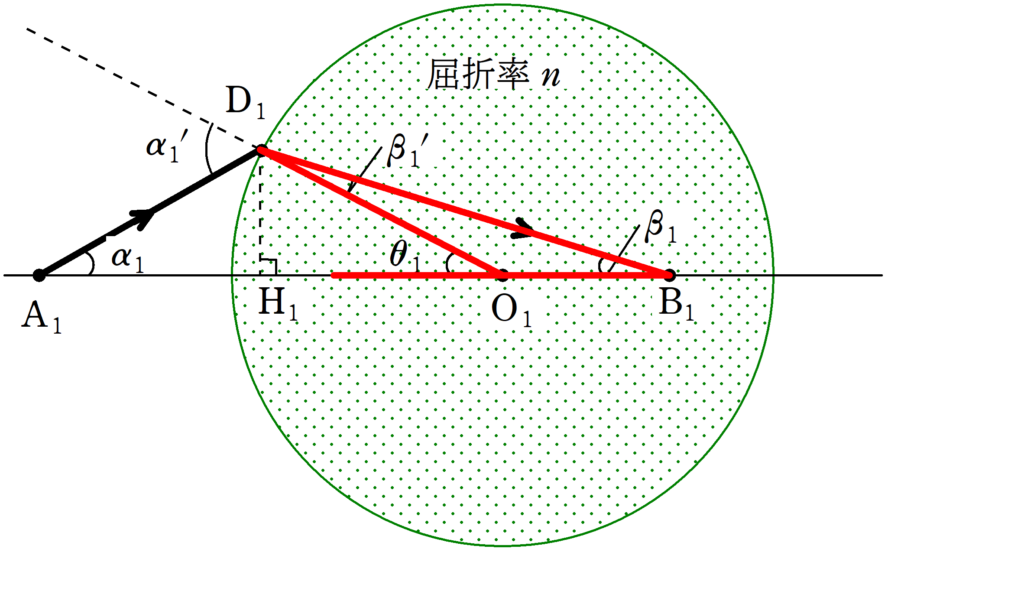
同じく,上図の赤色で囲まれた三角形の内角と外角の関係より
$\theta_{1}=\beta_{1}+\beta_{1}^{\prime}$
$\therefore$ $\beta_{1}^{\prime}=\theta_{1}-\beta_{1}$ (答)
(4)
(2)の$\alpha_{1}^{\prime}=\alpha_{1}+\theta_{1}$と(3)の$\beta_{1}^{\prime}=\theta_{1}-\beta_{1}$を(1)の$\alpha_{1}^{\prime}=n\beta_{1}^{\prime}$に代入して
$\alpha_{1}+\theta_{1}=n(\theta_{1}-\beta_{1})$ (答)
(5)(6)(7)
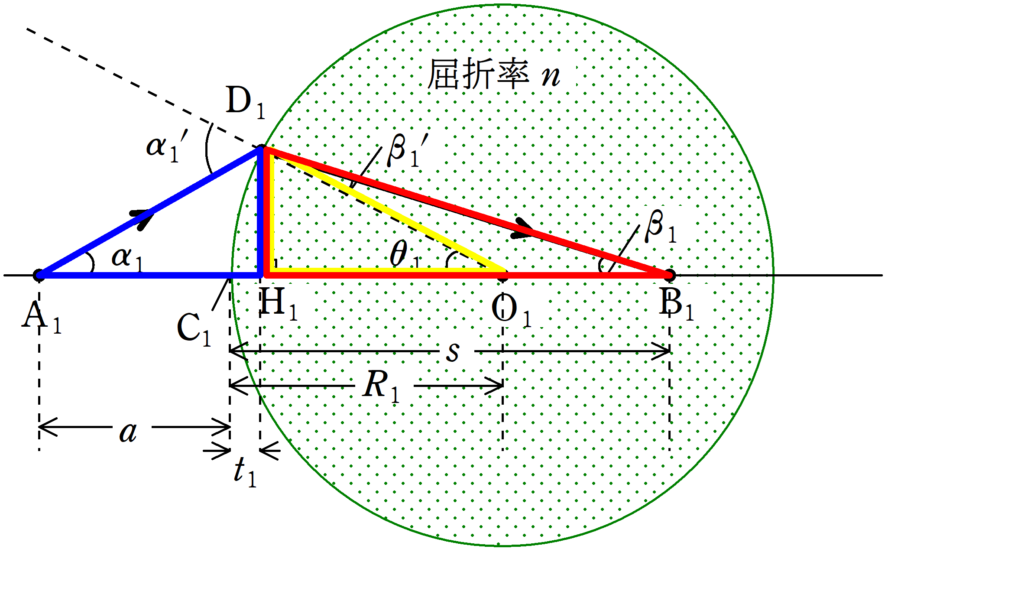
いずれも$t_{1}\fallingdotseq 0$として,上図の青の直角三角形,赤の直角三角形,黄色の直角三角形の正接($\tan$)を考え,「角度$\delta$が非常に小さいとき,$\sin\delta\fallingdotseq \tan\delta \fallingdotseq\delta$」の近似を用いると
$\tan\alpha_{1}\fallingdotseq \dfrac{\rm D_{1}H_{1}}{a}$ $\therefore$ $\alpha_{1}\fallingdotseq\dfrac{\rm D_{1}H_{1}}{a}$ (答)
$\tan\beta_{1}\fallingdotseq \dfrac{\rm D_{1}H_{1}}{s}$ $\therefore$ $\beta_{1}\fallingdotseq\dfrac{\rm D_{1}H_{1}}{s}$ (答)
$\tan\theta_{1}\fallingdotseq \dfrac{\rm D_{1}H_{1}}{R_{1}}$ $\therefore$ $\theta_{1}\fallingdotseq\dfrac{\rm D_{1}H_{1}}{R_{1}}$ (答)
(8)
(5)(6)(7)の$\alpha_{1}\fallingdotseq\dfrac{\rm D_{1}H_{1}}{a}$,$\beta_{1}\fallingdotseq\dfrac{\rm D_{1}H_{1}}{s}$,$\theta_{1}\fallingdotseq\dfrac{\rm D_{1}H_{1}}{R_{1}}$を(4)の$\alpha_{1}+\theta_{1}=n(\theta_{1}-\beta_{1})$に代入して
$\eqalign{\dfrac{\rm D_{1}H_{1}}{a}+\dfrac{\rm D_{1}H_{1}}{R_{1}}&=n\left(\dfrac{\rm D_{1}H_{1}}{R_{1}}-\dfrac{\rm D_{1}H_{1}}{s}\right)\cr \dfrac{1}{a}+\dfrac{1}{R_{1}}&=n\left(\dfrac{1}{R_{1}}-\dfrac{1}{s}\right)\cr \dfrac{1}{a}+\dfrac{n}{s}&=\dfrac{n-1}{R_{1}}}$
したがって,答えは$\dfrac{1}{a}+\dfrac{n}{s}=\dfrac{n-1}{R_{1}}$
(9)
(1)と同様の近似をします.
屈折の法則,$n\sin\beta_{2}^{\prime}=\sin\alpha_{2}^{\prime}$より
$n\beta_{2}^{\prime}=\alpha_{2}^{\prime}$ (答)
(10)
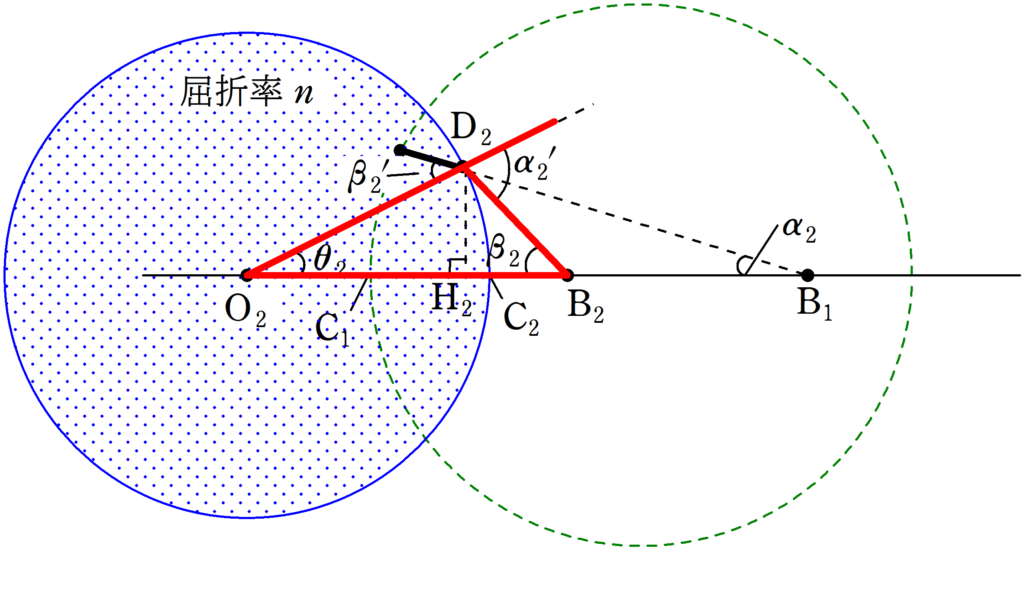
上図の赤色の三角形の内角と外角の関係より
$\alpha_{2}^{\prime}=\beta_{2}+\theta_{2}$ (答)
(11)
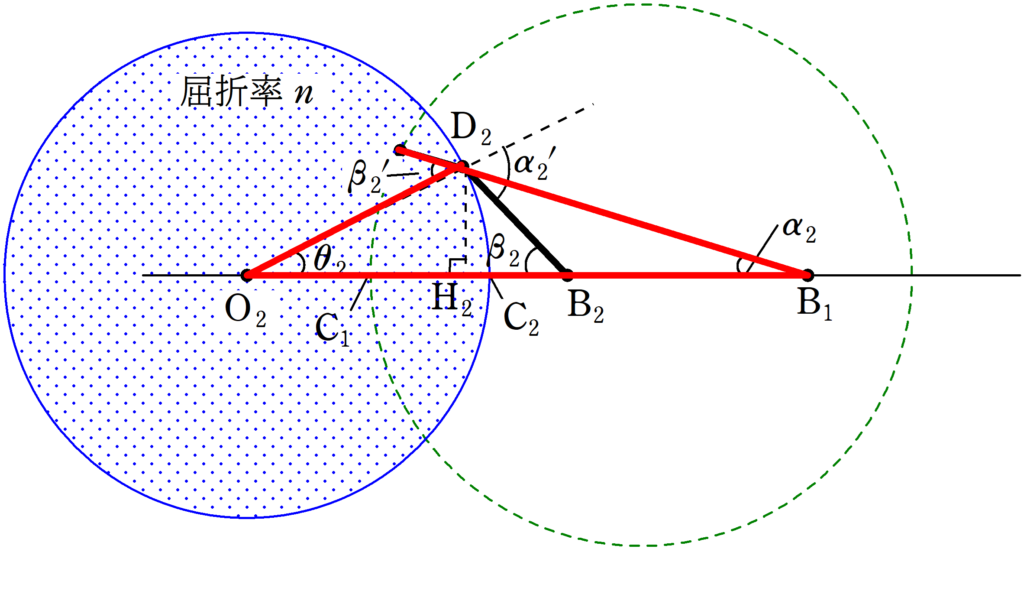
上図の赤色の三角形の内角と外角の関係より
$\beta_{2}^{\prime}=\alpha_{2}+\theta_{2}$ (答)
(12)
(10)の$\alpha_{2}^{\prime}=\beta_{2}+\theta_{2}$と(11)の$\beta_{2}^{\prime}=\alpha_{2}+\theta_{2}$を(9)の$n\beta_{2}^{\prime}=\alpha_{1}^{\prime}$に代入すると
$n(\alpha_{2}+\theta_{2})=\beta_{2}+\theta_{2}$ (答)
(13)(14)(15)
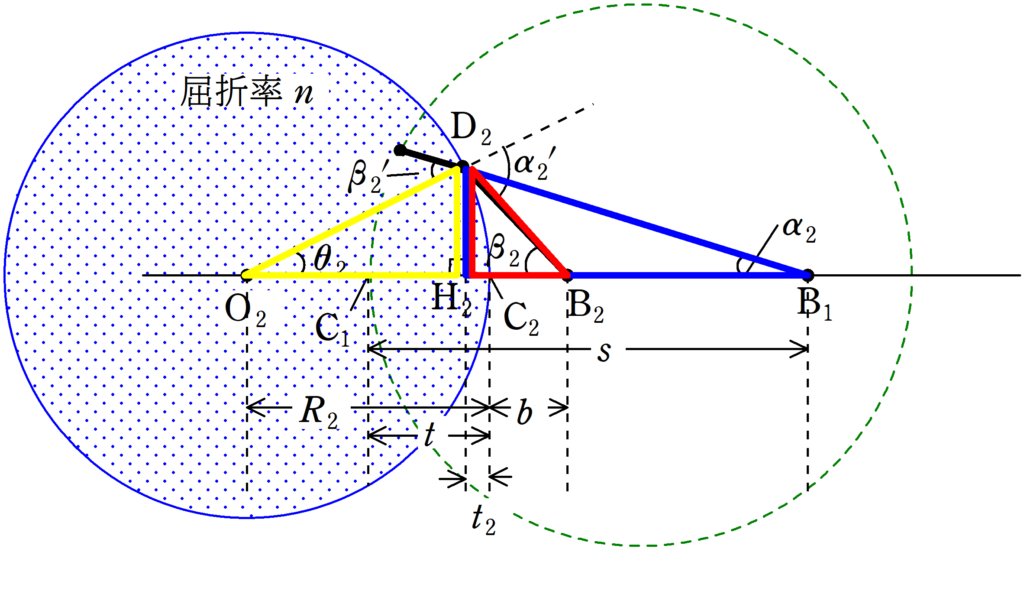
いずれも$t_{2}\fallingdotseq 0$,$t\fallingdotseq 0$として,上図の青の直角三角形,赤の直角三角形,黄色の直角三角形の正接($\tan$)を考え,「角度$\delta$が非常に小さいとき,$\sin\delta\fallingdotseq \tan\delta \fallingdotseq\delta$」の近似を用いると
$\tan\alpha_{2}\fallingdotseq \dfrac{\rm D_{2}H_{2}}{s}$ $\therefore$ $\alpha_{2}\fallingdotseq\dfrac{\rm D_{2}H_{2}}{s}$ (答)
$\tan\beta_{2}\fallingdotseq \dfrac{\rm D_{2}H_{2}}{b}$ $\therefore$ $\beta_{2}\fallingdotseq\dfrac{\rm D_{2}H_{2}}{b}$ (答)
$\tan\theta_{2}\fallingdotseq \dfrac{\rm D_{2}H_{2}}{R_{2}}$ $\therefore$ $\theta_{2}\fallingdotseq\dfrac{\rm D_{2}H_{2}}{R_{2}}$ (答)
(16)
(13)(14)(15)の$\alpha_{2}\fallingdotseq\dfrac{\rm D_{2}H_{2}}{s}$,$\beta_{2}\fallingdotseq\dfrac{\rm D_{2}H_{2}}{b}$,$\theta_{2}\fallingdotseq\dfrac{\rm D_{2}H_{2}}{R_{2}}$を(12)の$n(\alpha_{2}+\theta_{2})=\beta_{2}+\theta_{2}$に代入すると
$\eqalign{n\left(\dfrac{\rm D_{2}H_{2}}{s}+\dfrac{\rm D_{2}H_{2}}{R_{2}}\right)&=\dfrac{\rm D_{2}H_{2}}{b}+\dfrac{\rm D_{2}H_{2}}{R_{2}}\cr n\left(\dfrac{1}{s}+\dfrac{1}{R_{2}}\right)&=\dfrac{1}{b}+\dfrac{1}{R_{2}}\cr \dfrac{n}{s}&=\dfrac{1}{b}+\dfrac{1-n}{R_{2}}}$
したがって,答えは$\dfrac{n}{s}=\dfrac{1}{b}+\dfrac{1-n}{R_{2}}$
(17)
(8)の$\dfrac{1}{a}+\dfrac{n}{s}=\dfrac{n-1}{R_{1}}$と(16)の$\dfrac{n}{s}=\dfrac{1}{b}+\dfrac{1-n}{R_{2}}$から$s$を消去すると
$\eqalign{\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1-n}{R_{2}}&=\dfrac{n-1}{R_{1}}\cr \dfrac{1}{a}+\dfrac{1}{b}&=(n-1)\left(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}\right)}$
したがって,答えは$\dfrac{1}{a}+\dfrac{1}{b}=(n-1)\left(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}\right)$


コメント
[…] 屈折の法則によるレンズの式の導出 […]