[1]
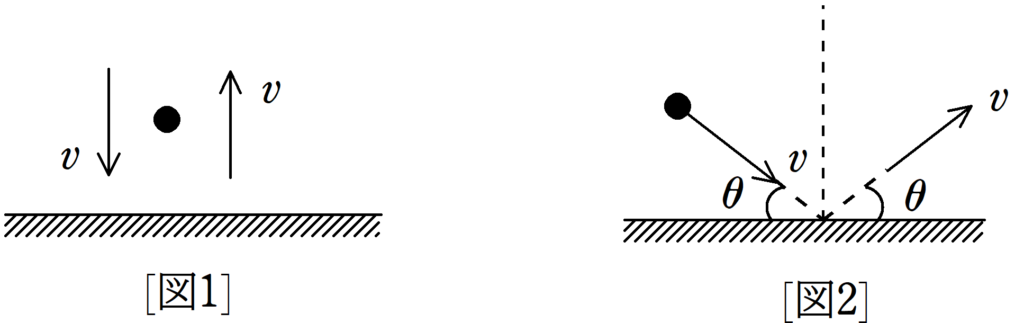
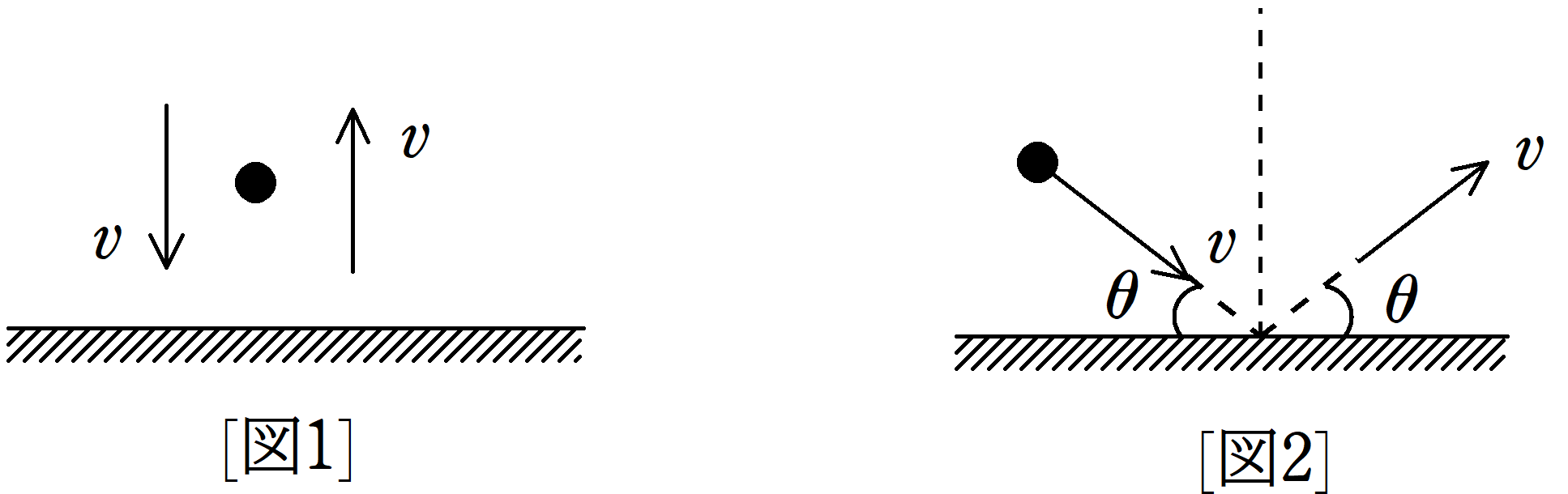
質量$m$の小物体が床と衝突することで受ける力積の大きさについて考える.[図1]のように,小物体は床に垂直に衝突し,床と衝突する直前の速さが$v$で,衝突した直後の速さが$v$であった.
このとき,小物体が受ける力積の大きさを計算せよ.
[2]
質量$m$の小物体が床と衝突することで受ける力積の大きさについて考える.[図2]のように,小物体が床と$\theta(0<\theta<\dfrac{\pi}{2})$の角度で衝突し,衝突後もなす角が$\theta$であった.衝突直前後の速さはともに$v$であるとき,衝突直前後で小物体が受ける力積の大きさを計算せよ.

今回は
運動量変化=力積
の式を使って問題を解いていきます.
時間$\varDelta t$の間の速度の変化を$\varDelta \vec{v}$とする.質量を$m$とすると
$m\varDelta \vec{v}=$力積
の関係がある.

注意して欲しいのは,$\varDelta \vec{v}$は「速さの変化」ではなく,「速度の変化」であるということです.
(1)

図1の上向きを正としましょう.
すると,衝突後の運動量は$mv$,衝突前の運動量は$m\cdot (-v)$となります.
したがって,運動量変化は
$mv-m\cdot (-v)=2mv$
となります.
この計算より,小物体が受ける力積の大きさは$2mv$(答)で,その向きは図1の上向きとなります.
(2)
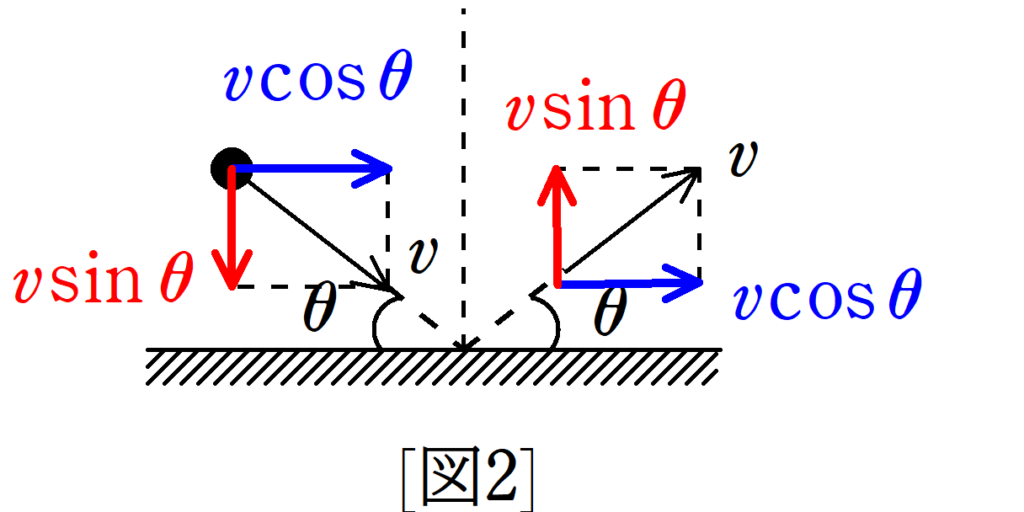

運動量はベクトルです.なので,上図のように成分分けして考えましょう.
衝突の直前後で床と水平な成分$v\cos\theta$は変化しません.
したがって,この成分は力積を受けません.
一方,鉛直成分は,鉛直下向きにの速度から鉛直上向きの速度に変化しています.その大きさはどちらも$v\sin\theta$です.
(1)と同様に考えて鉛直上向きを正とすると,運動量変化は
$mv\sin\theta-m\cdot (-v\sin\theta)=2mv\sin\theta$
したがって,小物体が受ける力積の大きさは$2mv\sin\theta$(答)で,向きは鉛直上向きです.

これからも,向きには十分注意して計算をしてください.


コメント
[…] […]