
2021年共通テスト第2問Bで出題された「2つの導体棒の運動」を題材に次の問題を解いてみましょう.
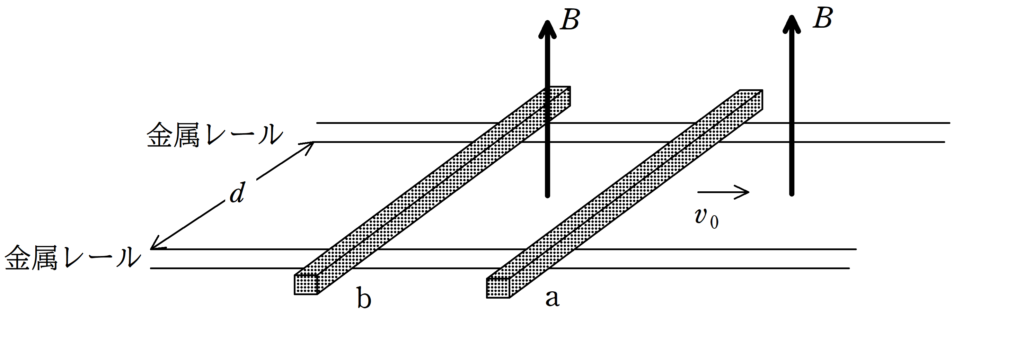
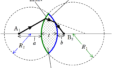
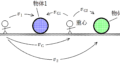
上図のように,鉛直上向きで磁束密度の大きさ$B$の一様な磁場(磁界)中に,十分長い2本の金属レールが水平面内に間隔$d$で平行に固定されている.その上に導体棒a,bをのせ,静止させた.導体棒a,bの質量は等しく,単位長さあたりの抵抗値は$r$である.導体棒はレールと垂直に保ったまま,レール上を摩擦なく動くものとする.また,自己誘導の影響とレールの電気抵抗は無視できる.
時刻$t=0$に導体棒aにのみ,右向きの初速度$v_{0}$を与えた.
(1) 導体棒が動き出した直後に導体棒aに流れる誘導電流の大きさ$i_{0}$を$B$,$d$,$v_{0}$,$r$から必要なものを用いて表せ.
(2) 時刻$t$において,導体棒a,bの速度はそれぞれ$v_{1}$,$v_{2}$であるとき,加速度は$a_{1}$,$a_{2}$であった.導体棒a,bの質量がともに$m$であるとき,運動方程式を立てることで,導体棒a,bの運動量の和が一定になることを示せ.
(3) (2)の運動方程式より,導体棒aが動き始めてから十分時間が経ったときの導体棒a,bの速度をそれぞれ求めよ.
<解答>
(1)

導体棒が磁場中を動くと起電力が生じるんだったね.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$

導体棒は初速度$v_{0}$で動き始めるので,誘導起電力の大きさは$v_{0}Bd$です.
導体棒の問題は次の3つの式を意識しましょう.
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式

キルヒホッフ則を立てますが,導体棒a,bの抵抗に注意です.
抵抗は$r$ではありません.
「単位長さあたりの抵抗が$r$」と書いてあるので,金属レール間の距離$d$の抵抗を考えて,$dr$となります.
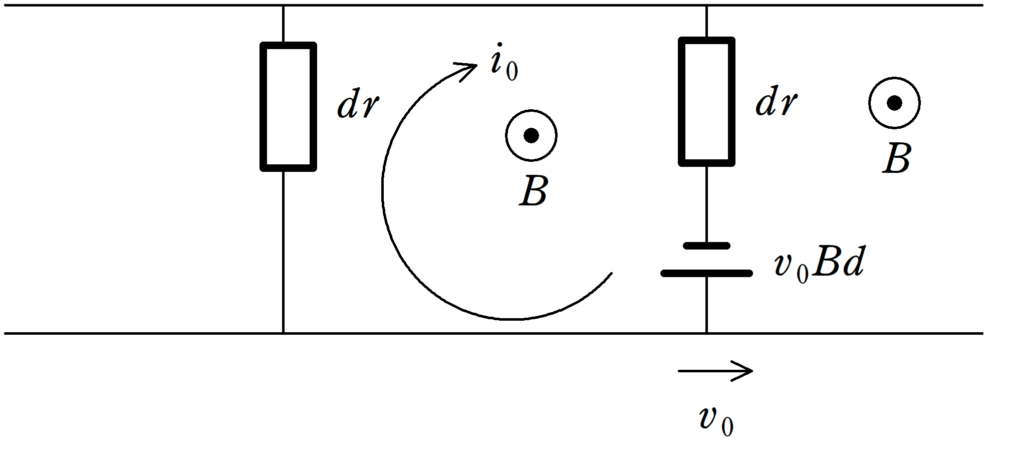

誘導起電力の向きはレンツの法則より,上図のようになります.
したがって,電流の向きは上図のような向きにとり,その大きさを$i$としましょう.
★ キルヒホッフ則
$\eqalign{v_{0}Bd-dr\cdot i-dr\cdot i&=0\cr2dri&=v_{0}Bd\cr i&=\dfrac{v_{0}B}{2r}}$
したがって,$i=\dfrac{v_{0}B}{2r}$
(2)
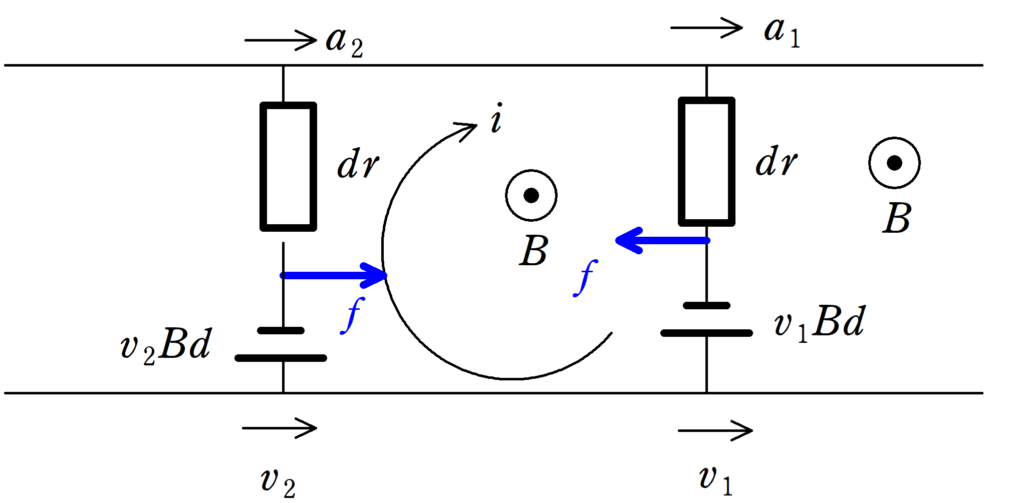

問題設定通りの速度と加速度で考えていきます.
導体棒a,bに生じる誘導起電力はそれぞれ,$v_{1}Bd$,$v_{2}Bd$となります.
回路に流れる電流を$i$としてキルヒホッフ則を立てましょう.
★ キルヒホッフ則
$\eqalign{v_{1}Bd-v_{2}Bd-dr\cdot i-dr\cdot i&=0\cr i&=\dfrac{v_{1}-v_{2}}{2r}B \dots (\ast)}$

さらに電流が流れることで導体棒a,bには電磁力がはたらきます.
電磁力の大きさを$f$とすると,流れる電流が$i$であることから
$f=iBd$
$(\ast)$を代入して
$\eqalign{f&=\dfrac{v_{1}-v_{2}}{2r}B\cdot Bd\\&=\dfrac{v_{1}-v_{2}}{2r}B^{2}d \dots(2\ast)}$
となります.
さらに,運動方程式より
★ 運動方程式
$ma_{1}=-f$ $\dots (3\ast)$
$ma_{2}=f$ $\dots (4\ast)$
$(3\ast)+(4\ast)$を計算して
$ma_{1}+ma_{2}=0$
さらに,$\dfrac{\Delta v_{1}}{\Delta t}$,$\dfrac{\Delta v_{2}}{\Delta t}$を上式に代入すると
$m\dfrac{\Delta v_{1}}{\Delta t}+m\dfrac{\Delta v_{2}}{\Delta t}=0$
両辺$\Delta t$を代入して
$m\Delta v_{1}+m\Delta v_{2}=0$

上式より,運動量の変化の和が0であることがわかったね.
(3)

今度は$(3\ast)-(4\ast)$を計算してみましょう.
$ma_{1}=-f$ $\dots (3\ast)$と$ma_{2}=f$ $\dots (4\ast)$の差をとって
$m(a_{1}-a_{2})=-2f$
この式に$f=\dfrac{v_{1}-v_{2}}{2r}B^{2}d$を代入すると
$\eqalign{m(a_{1}-a_{2})&=-2\cdot \dfrac{v_{1}-v_{2}}{2r}B^{2}d\\&=-\dfrac{B^{2}d}{r}(v_{1}-v_{2})}$
ここで,$a^{\prime}=a_{1}-a_{2}$,$v^{\prime}=v_{1}-v_{2}$とおけば
$ma^{\prime}=-\dfrac{B^{2}d}{r}v^{\prime}$ $\dots (5\ast)$

$(5\ast)$は終端速度型の運動方程式だね.
つまり,十分時間が経つと,加速度$a^{\prime}=0$となるよ.
質量を$m$,加速度を$a$,速度を$v$,$C$を定数とすると
$ma=-kv+C$
は終端速度型の運動方程式である.
終端速度型の運動方程式は次の特徴がある.
十分時間が経つと,速度が一定(加速度が0)になる.
速度が一定になったときの速度を終端速度という.
終端速度は運動方程式に$a=0$を代入して
$0=-kv+C$ $\therefore v=\dfrac{C}{k}$
また,$t=0$のときの速度を$v_{0}$とすると,そのときの加速度($v-t$グラフの傾き)は
$a=\dfrac{-kv_{0}+C}{m}$
となる.

十分時間が経つと,$a^{\prime}=0$となるので,
$v^{\prime}=0$
すなわち
$v_{1}-v_{2}=0$ $\therefore v_{1}=v_{2}$
つまり,最終的には,2つの導体棒の速さは同じになるんだね.
その速さを$V$として,運動量保存則を立てましょう.
★ 運動量保存則
$mv_{0}=mV+mV$
$V=\dfrac{v_{0}}{2}$

今回の共通テストの問題のように,ある程度のヒントがないと,計算が大変なんだね.

コメント