
今回は[基本編]の最終回!浮力の単振動を扱います.ちなみに,[基本編]の後は[標準編]があります.
では,問題を解いてみましょう.
前回の内容です.
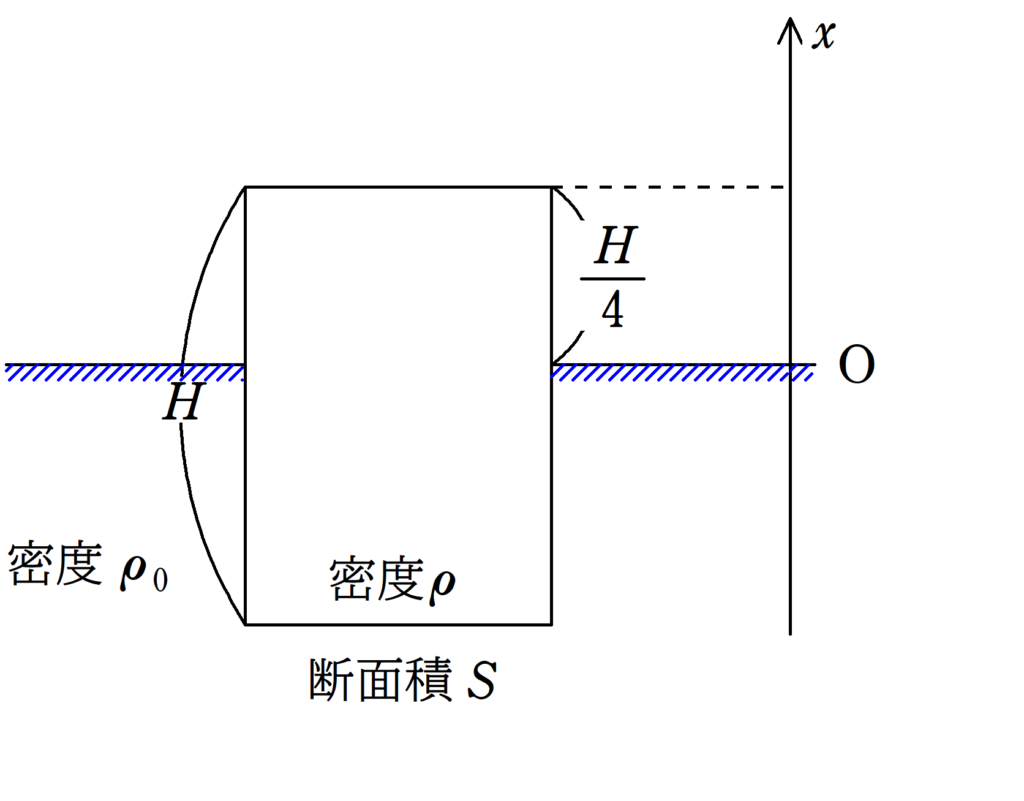
上図のように,密度$\rho_{0}$の液体の中に高さが$H$,底面積$S$の円柱がある.はじめ,何も力を加えないと,円柱の上面は液面より高さ$\dfrac{H}{4}$上にあった.重力加速度の大きさを$g$とする.
(1) 円柱のつり合いの式より,円柱の密度$\rho$を$\rho_{0}$を用いて表せ.
液面を原点として,鉛直上向きを正とした$x$軸をとる.円柱上面に力を加え,$\dfrac{H}{12}$下に下げて静かに手をはなしたところ,円柱は単振動をした.ただし,単振動している間は液体からの抵抗力は無視し,液面の高さは振動によって変化しないものとしてよい.以下,円柱の座標は上面の位置$x$で表すものとする.
(2) 単振動の中心座標$x_{0}$,角振動数$\omega$,周期$T$を$S$,$g$,$H$から必要なものを用いて表せ.
(3) 運動をはじめた時刻を$t=0$とする.時刻$t$における円柱の座標$x$を$S$,$g$,$H$,$t$から必要なものを用いて表せ.
<解答>
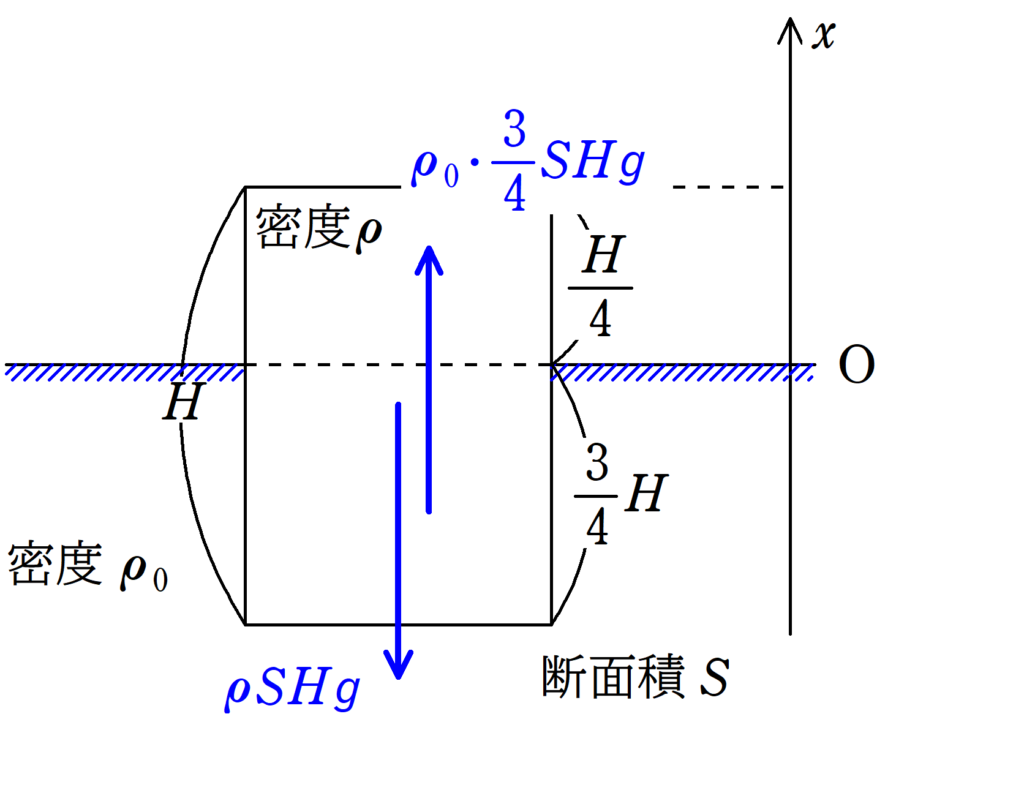
(1) 円柱にはたらく重力と浮力のつり合いを考えます.ちなみに,
(質量)=(密度)×(体積)
です.たとえば,次のような単位のときを考えてみましょう.
質量 [$\rm{kg}$],密度[$\rm{kg/m^{3}}$],体積[$\rm{m^3}$]とすると,
$\rm{\dfrac{kg}{\cancel{m^3}}\cdot \cancel{m^3}}$
のように,密度と体積の積の単位は$[\rm{kg}]$になっています.
さらに,浮力$F$は,アルキメデスの原理より“浮力の大きさは液体や気体をおしのけた分の重さ”となります.今回,液体をおしのけた分の重さは
$\rho_{0}S\cdot \dfrac{3}{4}Hg$
です.円柱がつり合うように,鉛直上向きにはたらきます.
円柱の鉛直方向のつり合いの式より
$\rho SHg=\dfrac{3}{4}\rho_{0}SHg$ $\therefore$ $\rho =\dfrac{3}{4}\rho_{0}$
となります.
(2)
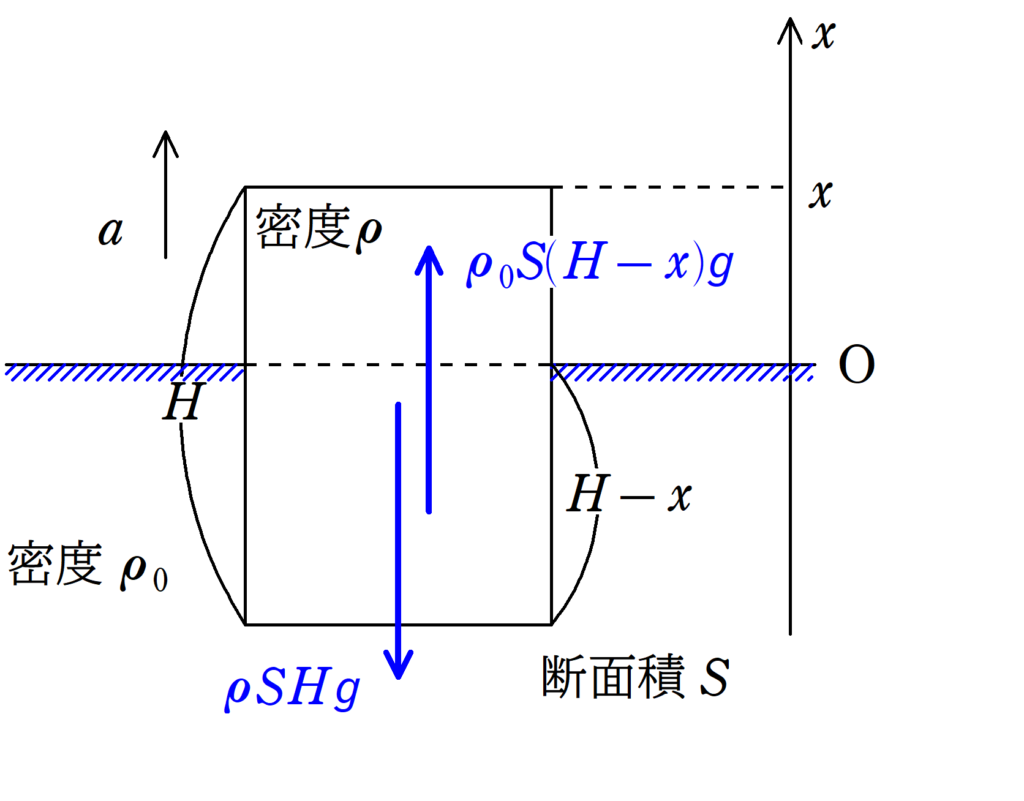
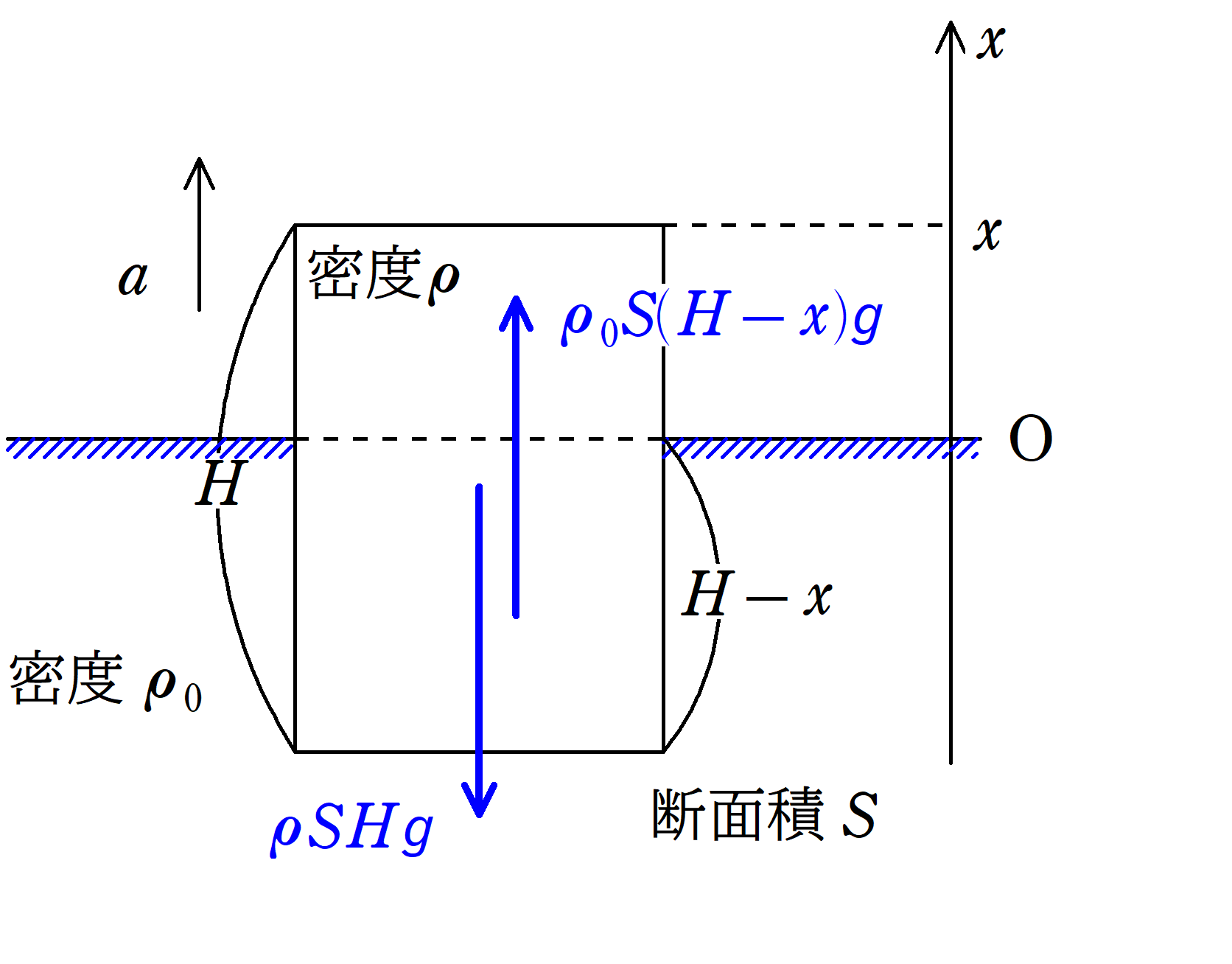
次にどのような単振動をしているかを調べるために,運動方程式を立ててみましょう.今回は問題の設定上,円柱の上面を基準に座標を考えていますが,特に指定がなかったらどこを基準に考えてもよいです.ただ,あまり面倒なところで設定すると後で苦労するので,上面か下面,重心あたりがよいでしょう.
上面の位置が$x$のとき,液体に浸っている部分の体積は$H-x$なので,浮力の大きさは$\rho_{0}S(H-x)g$です.また,重力は変化せず,$\rho SHg$ですが,(1)より,$\rho$を$\rho_{0}$で表すと,$\dfrac{3}{4}\rho_{0}SHg$となります.
$x$軸の正の向きに加速度$a$を設定すると,運動方程式は
$\eqalign{\dfrac{3}{4}\rho_{0}SHa&=\rho_{0}S(H-x)g-\dfrac{3}{4}\rho_{0}SHg\\&=-\rho_{0}Sgx+\dfrac{1}{4}\rho_{0}SHg\\&=-\rho_{0}Sg\left(x-\dfrac{1}{4}H\right)}$
この運動方程式より,中心座標は$x_{0}=\dfrac{1}{4}H$となります.角振動数$\omega$は
$\omega=\sqrt{\dfrac{\rho_{0}Sg}{\dfrac{3}{4}\rho_{0}SH}}=\sqrt{\dfrac{4g}{3H}}$
したがって,周期$T$は
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{3H}{4g}}$
※ 4をルートの外に出してもかまいません.
周期のルートの中に注目してみてください.ルートの中が(長さ)÷(加速度)の単位になっています.これは単振り子の運動でも同じ形になっています.このように,次元が見えてくると,物理における計算ミスがなくなっていきます.
(3) 中心座標が$x_{0}=\dfrac{1}{4}H$ということが(2)からわかりました.これは円柱に力を加えていないときです.ここから$\dfrac{1}{12}H$下げて静かに手をはなすので,ここが下端となります.つまり,振幅$A$は$\dfrac{1}{12}H$となります.最下点からスタートして$x$軸の正の向きにスタートするので$-\cos$型ですね.以上より,時刻$t$における円柱の上面の位置$x$は
$x=x_{0}-A\cos \omega t=\dfrac{1}{4}H-\dfrac{1}{12}H\cos\sqrt{\dfrac{4g}{3H}}t$
となります.

以上で単振動の[基本編]は終了です.[基本編]では一貫して,
- 運動方程式を立てる
- 中心座標,角振動数,周期を求める
- 初期条件から時刻$t$における座標$x$を求める
という練習をしてきました.標準編になってもこの基本はでてきます.次回から[標準編]です.速度や加速度の導出の計算や座標と時刻の関係式の計算練習,力学以外での単振動について扱います.
次回の記事です.




コメント
[…] […]
[…] 波の式といえば,多くの人が嫌がるところなのではないでしょうか.そもそも $y=Asin {2pi (dfrac{t}{T}-dfrac{x}{lambda})}$ $dots (ast)$ の式は何を意味して… [基本]単振動の演習問題⑧ 運動方程式を立てる4 [基本]単振動の演習問題⑩ 運動方程式を立てる6 […]
[…] [基本]単振動の演習問題⑩ 運動方程式を立てる6NEKO今回はの最終回!浮力… […]