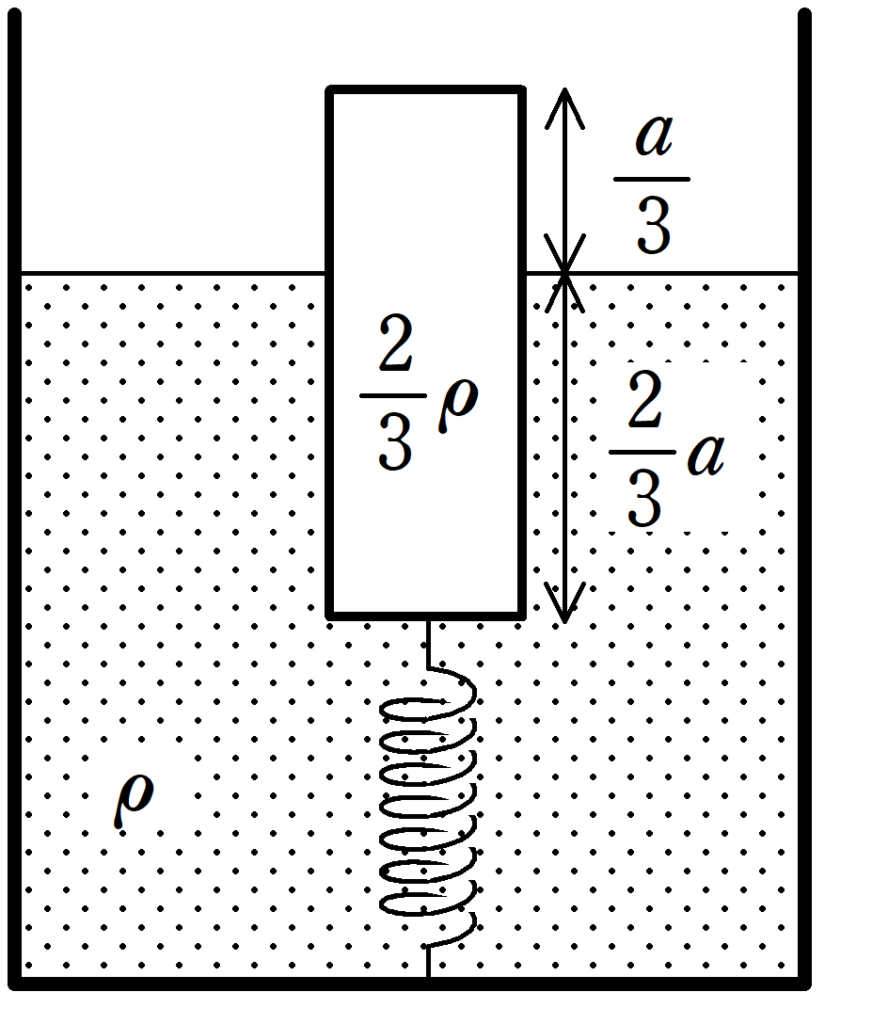
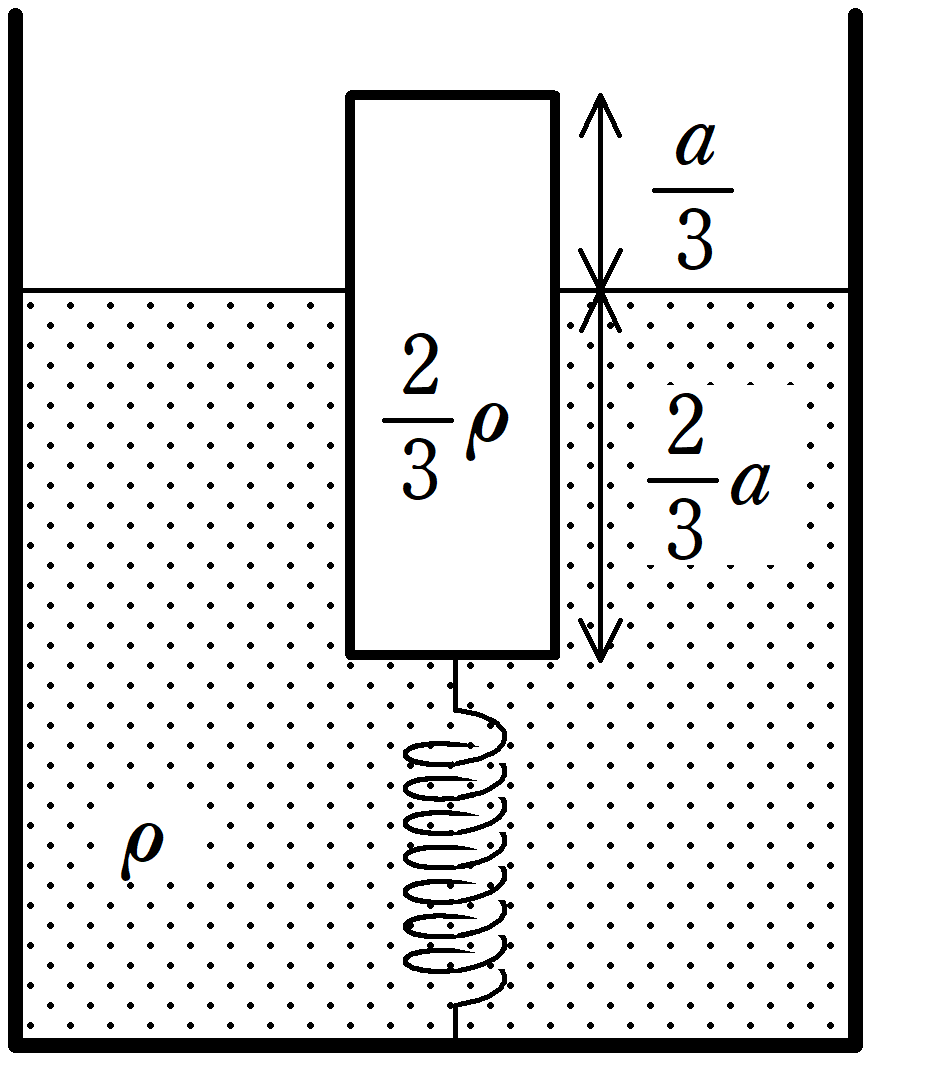
底面積$S$,高さ$a$,一様な密度$\dfrac{2}{3}\rho$の円柱物体がある.
この円柱物体にばね定数$k$の軽いばねをつなげ,ばねの他端は密度$\rho$の液体の底に固定する.
はじめ,円柱物体の$\dfrac{2}{3}a$の部分は液体中にあり,$\dfrac{a}{3}$の部分は空気中にあるとき,ばねは自然長であった.
この状態から,円柱物体の上面に力加え,$\dfrac{a}{6}$だけ上に持ち上げ,静かに手をはなすと,円柱物体は単振動をはじめた.
ただし,液体および空気による抵抗は無視をし,円柱物体は鉛直方向のみに振動する.また,単振動をすることによって,液面の高さは変化しないものとしてよい.
重力加速度の大きさを$g$として次の問いに答えよ.
(1) 円柱物体の上面と液面の距離が$x$のとき,鉛直上向きの加速度を$\beta$として,円柱物体の運動方程式を立てよ.
(2) 振動の周期$T$を求めよ.
(3) 単振動の振幅$A$を求めよ.
(4) 円柱物体の最大の速さ$v$を求めよ.
<解答>
(1)
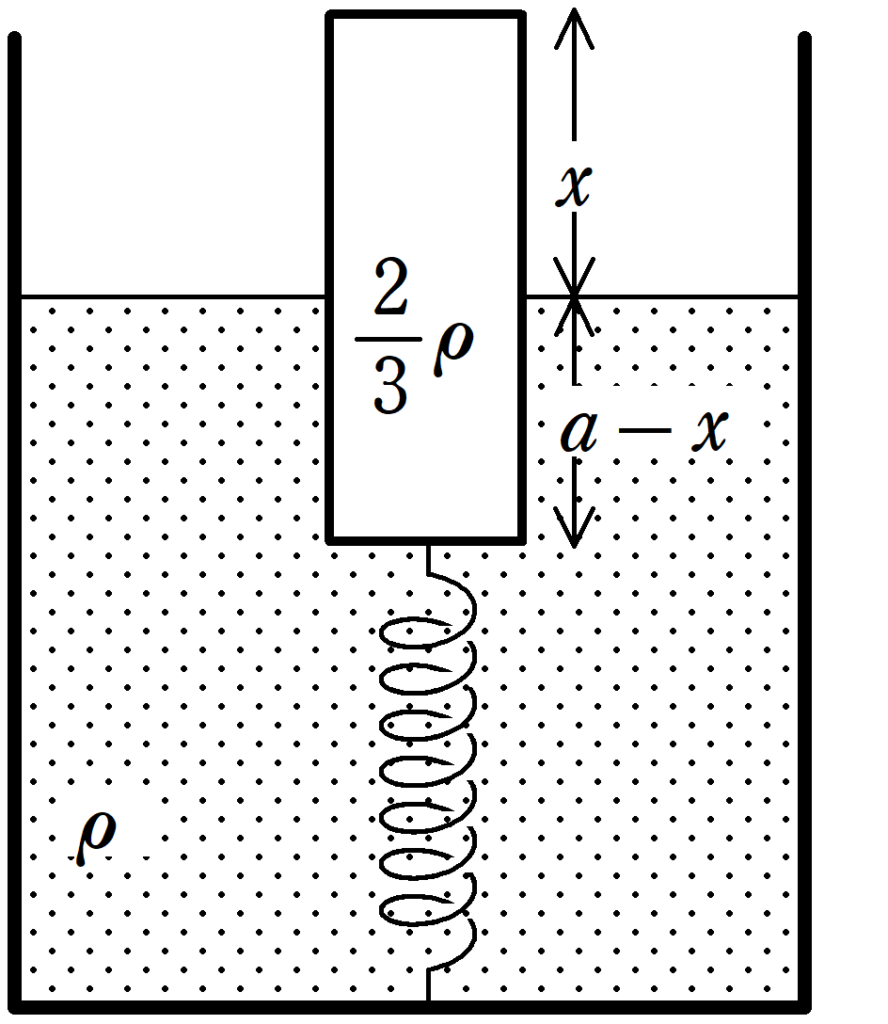

まずは,上面が液面より高さ$x$であるときの運動方程式を立ててみましょう.
その運動方程式から,振動の中心や角振動数や周期を求めることができます.
円柱物体にはたらく力は重力,浮力,弾性力がありますね.
浮力は液体に入っている部分のみはたらくことに注意です.
物体の質量を$m$,一様な密度を$\rho$,体積を$V$とする.このとき,次の関係がある.
$m=\rho V$
物体がおしのけた液体(または気体)の重さの分だけ浮力が鉛直上向きにはたらく.(重力加速度が鉛直下向きにはたらいているとき)
密度$\rho_{0}$の液体(または気体)中に体積$V$の物体があり,重力加速度の大きさを$g$とするとき,浮力の大きさ$F_{0}$は
$F_{0}=\rho_{0}Vg$
質量を$m$,加速度を$a$,物体の座標を$x$,$x_{0}$を定数,$k$を正の定数とする.
運動方程式が以下で表されている.
$ma=-k(x-x_{0})$
このとき,振動の中心は$x_{0}$,角振動数$\omega$と周期$T$は次のようになる.
$\omega=\sqrt{\dfrac{k}{m}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{k}}$
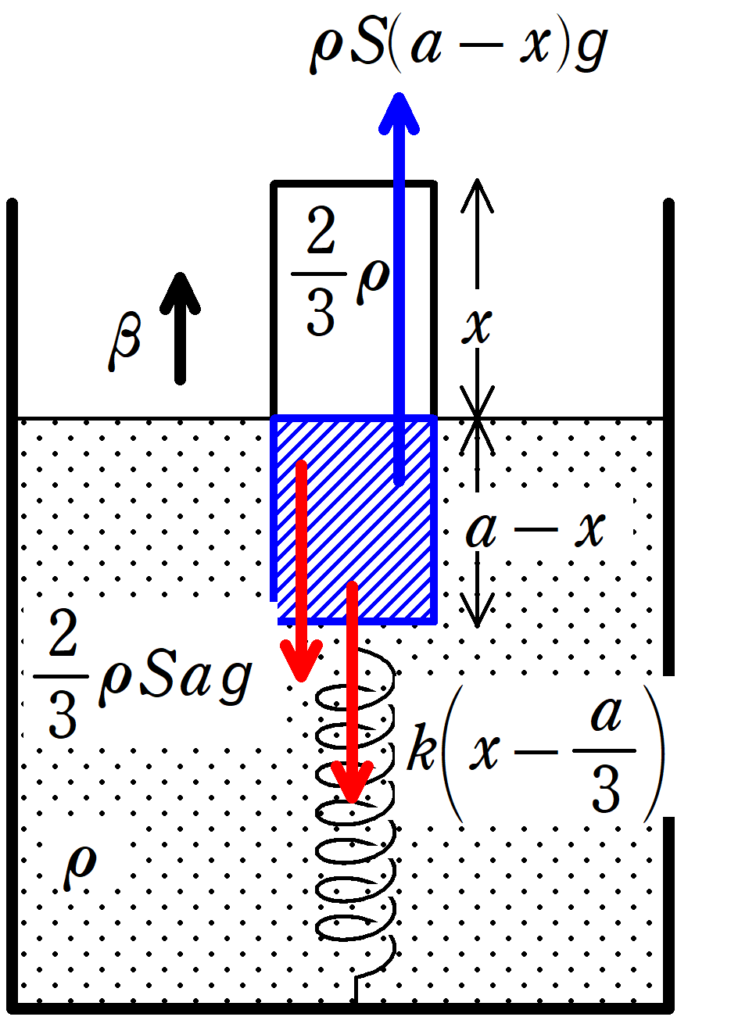

加速度を鉛直上向きに$\beta$としましょう.
円柱物体の質量$m$は
$m=\dfrac{2}{3}\rho Sa$
また,液体に入っている部分の体積が$S(a-x)$なので,浮力の大きさ$F_{0}$は
$F_{0}=\rho S(a-x)g$
となります.
さらに,弾性力は伸びているときを考えて,
$k(x-\dfrac{a}{3})$
★ 運動方程式
$\eqalign{\dfrac{2}{3}\rho Sa\beta&=\rho S(a-x)g-\dfrac{2}{3}\rho Sag-k(x-\dfrac{a}{3})\\&=\rho Sag-\rho Sgx-\dfrac{2}{3}\rho Sag-kx+\dfrac{a}{3}k\\&=-(\rho Sg+k)x+\dfrac{1}{3}\rho Sag+\dfrac{1}{3}ka\\&=-(\rho Sg+k)x+\dfrac{a}{3}(\rho Sg+k)\\&=-(\rho Sg+k)(x-\dfrac{a}{3})}$
したがって,答えは$\dfrac{2}{3}\rho Sa\beta=-(\rho Sg+k)(x-\dfrac{a}{3})$
(2)

この運動方程式から,振動の中心$x_{0}$と周期$T$はそれぞれ
$x_{0}=\dfrac{a}{3}$
$\eqalign{T&=2\pi\sqrt{\dfrac{\dfrac{2}{3}\rho Sa}{\rho Sg+k}}\\&=2\pi\sqrt{\dfrac{2\rho Sa}{3(\rho Sg+k)}}}$
となります.
したがって,振動の周期は$T=2\pi\sqrt{\dfrac{2\rho Sa}{3(\rho Sg+k)}}$
(3)

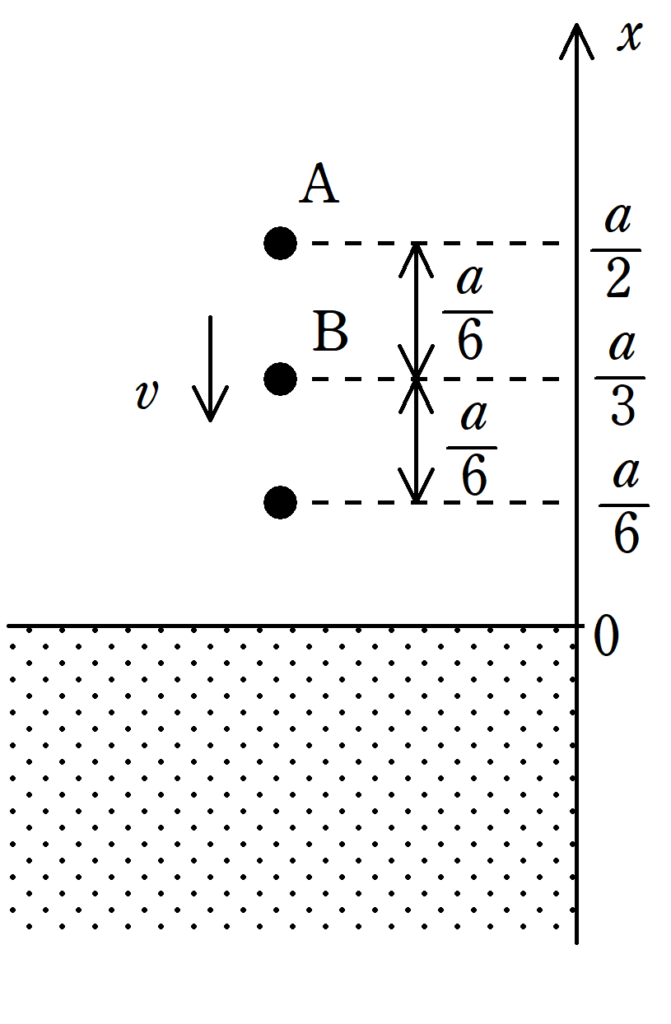
(2)から,はじめの状態が振動の中心であることが判明しました.
はじめの状態から$\dfrac{a}{6}$だけ上に持ち上げて,静かにはなしたので,手をはなした位置が振動の上端となります.
上端と中心の距離が振幅なので,振幅$A$は$A=\dfrac{a}{6}$となります.
(4)

せっかく,運動方程式を立てたので,単振動のエネルギー保存則を立てて速さを求めましょう.
単振動において,速度が最大となるのは,中心にいるときです.
単振動の運動方程式が
$ma=-k(x-x_{0})$
になるとき,単振動のエネルギー保存
$\dfrac{1}{2}mv^{2}+\dfrac{1}{2}k(x-x_{0})^{2}=$一定
が成り立つ.
※ $(x-x_{0})^{2}$は中心からの距離の2乗を表している.自然長からの距離ではない.
※ 上記の運動方程式を変形したものなので,摩擦力や重力がはたらいてもその仕事をいれないでよい.
★ 単振動のエネルギー保存
振動の中心における速さを$v$として
$\eqalign{\dfrac{1}{2}\cdot \dfrac{2}{3}\rho Sa \cdot 0^{2}+\dfrac{1}{2}(\rho Sg+k)(\dfrac{a}{6})^{2}&=\dfrac{1}{2}\cdot \dfrac{2}{3}\rho Sa \cdot v^{2}+\dfrac{1}{2}(\rho Sg+k)\cdot 0^{2}\cr \dfrac{1}{2}\cdot \dfrac{2}{3}\rho Sa\cdot v^{2}&=\dfrac{1}{2}(\rho Sg+k)\cdot (\dfrac{a}{6})^{2}\cr v^{2}&=\dfrac{\rho Sg+k}{2}\cdot \dfrac{a^{2}}{36}\cdot 3\cdot \dfrac{1}{\rho Sa}\cr v^{2}&=\dfrac{a(\rho Sg+k)}{24\rho S}\cr v&=\dfrac{1}{2}\sqrt{\dfrac{a(\rho Sg+k)}{6\rho S}}}$
したがって,答えは$v=\dfrac{1}{2}\sqrt{\dfrac{a(\rho Sg+k)}{6\rho S}}$

コメント