<問題>

<解答>
| 単位 | 説明 | |
| 放射能の強さ | $\rm Bq$(ベクレル) | 1秒間あたりに崩壊する原子核の個数を$1\rm Bq$とする. |
| 吸収線量 | $\rm Gy$(グレイ) | 放射線が物質に吸収されるときに与えるエネルギー.物質$1\,\rm kg$が$1\,\rm J$のエネルギーを吸収するときの吸収線量を$1\,\rm Gy$とする. |
| 等価線量 | $\rm Sv$(シーベルト) | 吸収線量に,人体への影響を考慮した係数をかけた値.係数は放射線の種類によって異なる. |
| 実効線量 | $\rm Sv$(シーベルト) | 等価線量に,組織・器官ごとの影響を表す計数をかけ,すべての組織・器官で足し合わせた値. |
(1) 問題文に書かれているように,放射能の強さ$I\,[\rm Bq]$は,原子核の数$N$に比例し,その比例定数が$\dfrac{0.693}{T}\,[/\rm s]$なので
$I=\dfrac{0.693}{T}\times N$ $\cdots (\ast)$
また,アボガドロ定数は$6.02\times 10^{23}\,[/\rm mol]$より,(質量):(個数)の比例式をつくって
$238:6.02\times 10^{23}=1.00:N$ $\therefore\,\, N=\dfrac{6.02\times 10^{23}}{238}$
これと,半減期$T=1.42\times 10^{17}\,[\rm s]$を$(\ast)$に代入して
$I=\dfrac{0.693}{1.42\times 10^{17}}\times \dfrac{6.02\times 10^{23}}{238}\fallingdotseq 1.23\times 10^{4}\,[\rm Bq]$ (答)
(2) 物質$1\,\rm kg$が$1\,\rm J$のエネルギーを吸収するときの吸収線量を$1\,\rm Gy$としているので,$10\,\rm kg$の物体が吸収するエネルギーは
$10\times 1\,\rm J=10\,[\rm J]$ (答)
(3) 半減期の式は以下のまとめで確認
時刻$t=0$における放射性元素の数を$N_{0}$とする.時刻$t$における放射性元素の数を$N(t)$とする.半減期(放射性元素の数が半分になるまでの時間)を$T$とすると,次の式が成り立つ.
$N(t)=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}$
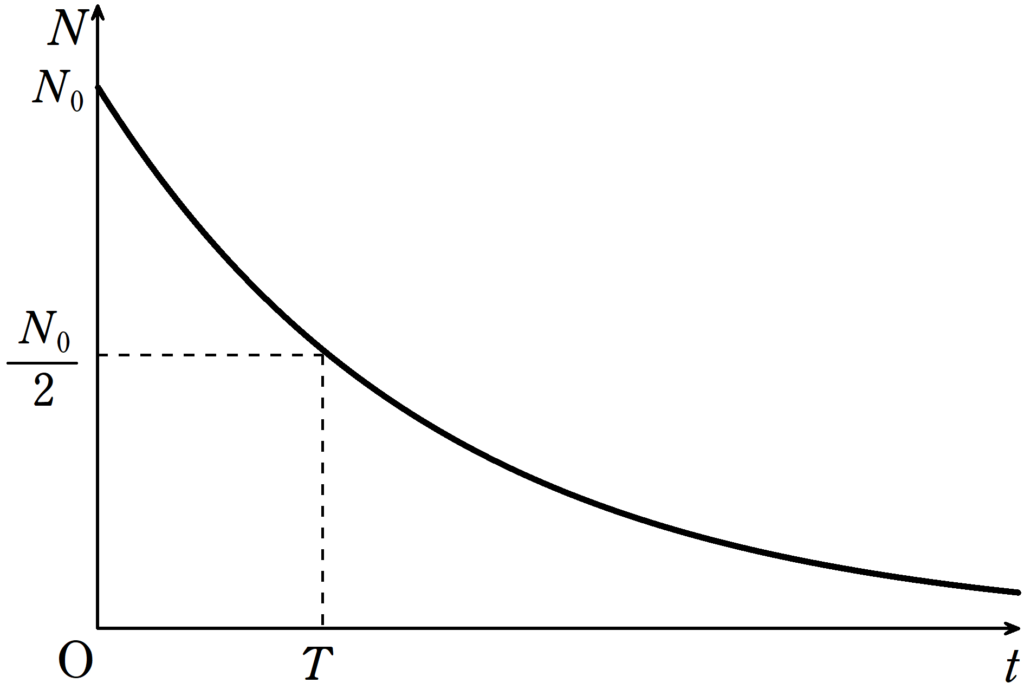
時刻$0$での放射性物質の原子核の個数$N_{0}$として,時刻$T$における放射性元素の個数$N_{t=T}$は半減期の式より
$N_{t=T}=N_{0}\left(\dfrac{1}{2}\right)^{\frac{T}{T}}=\dfrac{1}{2}N_{0}$ $\cdots (2\ast)$
また,時刻$t=3T$での放射性元素の個数$N_{t=3T}$は半減期の式より
$N_{t=3T}=N_{0}\left(\dfrac{1}{2}\right)^{\frac{3T}{T}}=\dfrac{1}{8}N_{0}$
だから,$t=T$から$t=3T$に崩壊した原子核の数は
$\dfrac{1}{2}N_{0}-\dfrac{1}{8}N_{0}=\dfrac{3}{8}N_{0}$
したがって,$t=0$から$t=T$までに崩壊した原子核の数は,$t=T$から$t=3T$に崩壊した原子核の数の
$\dfrac{1}{2}N_{0}\div \dfrac{3}{8}N_{0}=\dfrac{4}{3}$倍 (答)



コメント