
2022年の芝浦工業大で出た束縛条件を
用いた問題を扱います.
実際の試験では,ヒントがたくさんあり,解きやすいようにされていましたが,ヒントがないとして考えてみましょう.
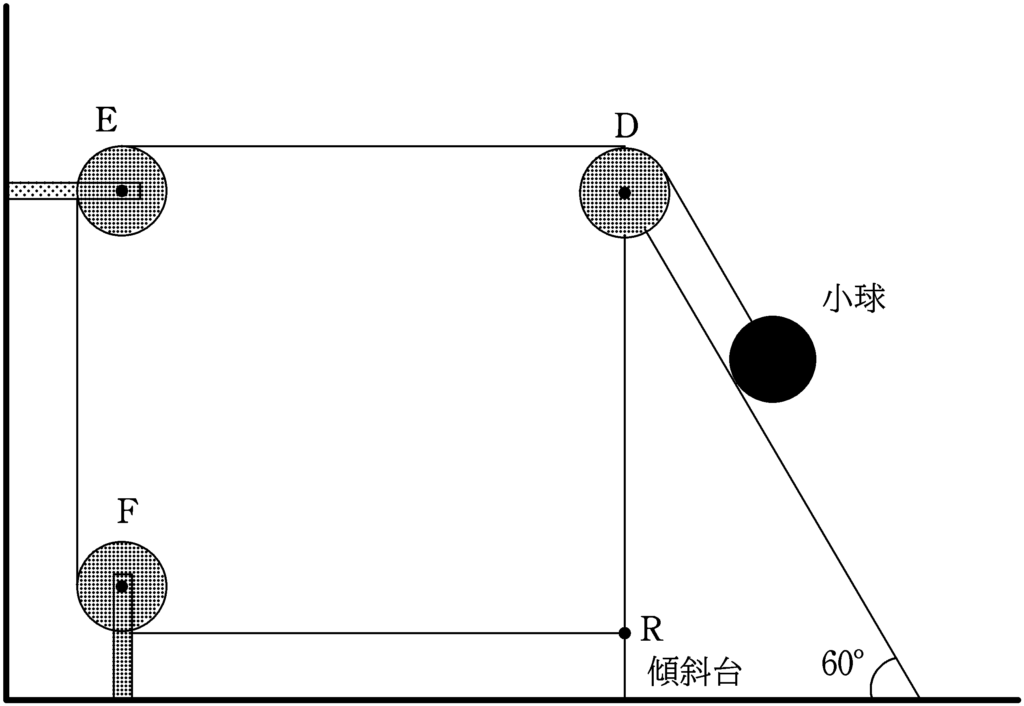
図のように,頂部に滑車Dが設置された水平面となす角度が$60^{\circ}$で質量$5m$の傾斜台を水平面上に固定せず置いた.また,糸を質量$m$のおもりにつなげて滑車Dを通し,定滑車Eと定滑車Fを経由させ,傾斜台の左側面上の、Rに固定した.さらに,小球が斜面上で静止するよう傾斜台を水平面と一時的に固定した.このとき,糸はたるむことなく,小球と滑車Dの間の糸は斜面と平行に張り,滑車DとEの間の糸と滑車Fと点Rの間の糸は水平方向に,滑車EとFの糸は鉛直方向に張った.傾斜台と水平面との固定を静かに外したところ,傾斜台は傾くことなく水平面上を左方向へなめらかに動き出し,小球は傾斜台を離れることなく滑り始めた.小球が水平面に達するまで,糸は運動中にたるむことはなく,運動中に摩擦はどこにもなかった.以下では,小球が水平面に達するまでの運動について考える.ただし,滑車の質量はすべて無視でき,なめらかに回るものとする.同様に,すべての糸の質量も無視することができ,糸は伸び縮みすることはない.傾斜台および小球は同一鉛直面内で運動し,重力加速度の大きさを$g$とする.また,空気抵抗は無視できるものとする.
(1) 台が水平左方向に$\varDelta X$変位したとき,小球は静止系からみて水平左方向に$\varDelta x$,鉛直下方向に$\varDelta y$変位した.糸の長さが一定であるという条件から$\varDelta x$を求めよ.ただし,答えには,$\varDelta X$,$\varDelta y$は使用しないこと.
(2) 小球が斜面を離れないことから,$\varDelta X$と$\varDelta y$の間の関係式を求めよ.
(3) Rの点で傾斜台を引く張力の大きさを$T$,小球と傾斜台の間にはたらく垂直抗力の大きさを$N$とする.傾斜台の水平左方向の加速度を$A$として,運動方程式を立てよ.
(4) 小球の鉛直下向きの加速度を$a_{y}$として,鉛直下方向の運動方程式を立てよ.
(5) $A,a_{y},T,N$を,$m$,$g$を用いて表せ.
<解答>
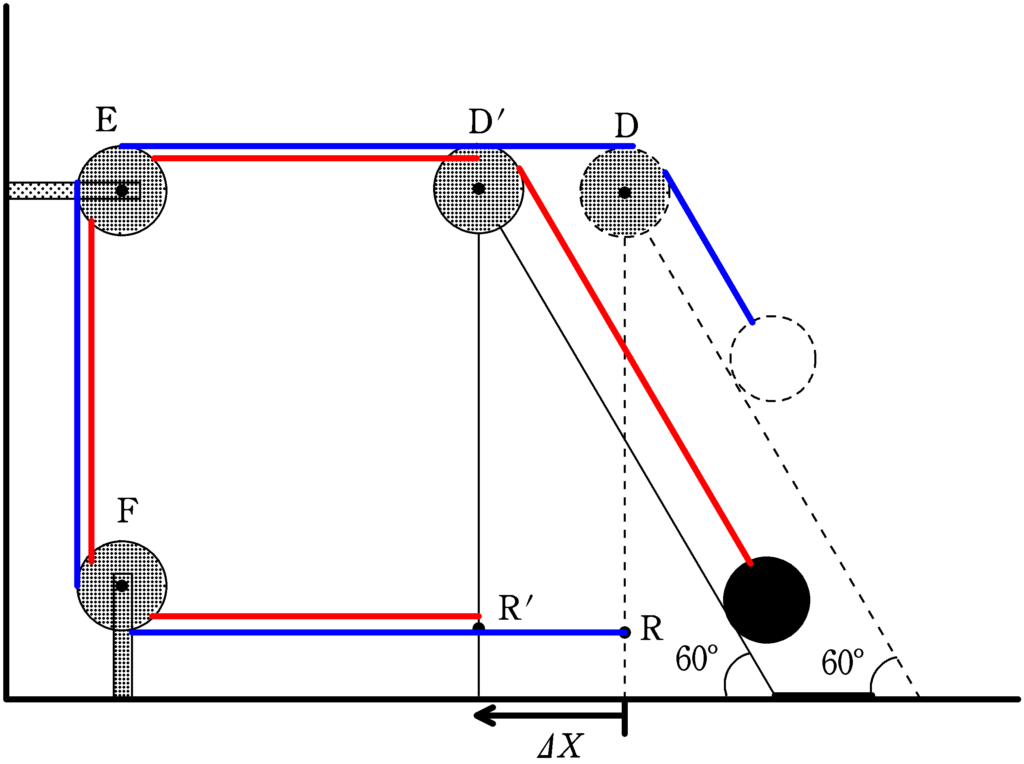
(1)

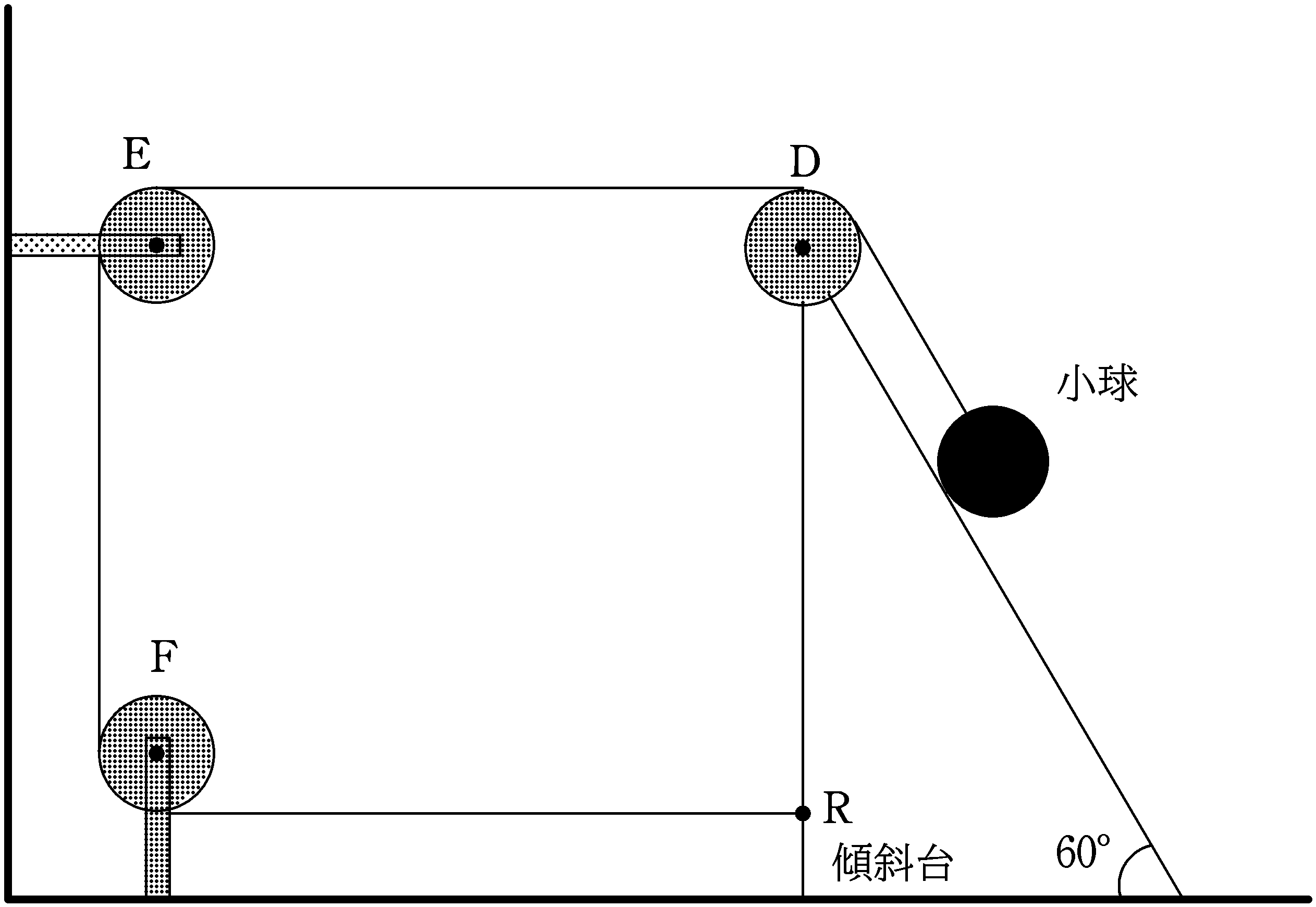
下図の点線が動く前,実線が動いた後です.
下図で確認すると,傾斜台が$\varDelta X$移動後,$\rm R’$から$\rm D’$は,移動前の$\rm R$から$\rm D$に比べて$2\varDelta X$だけ短くなっています.
糸の長さは一定なので,小球は傾斜台移動前に比べて斜面上を$2\varDelta X$だけ下っていることになります.

傾斜台が$(\varDelta X,0)$変位し,小球が$(\varDelta x,\varDelta y)$変位しているとき,傾斜台からみた小球の変位は次のようになります.
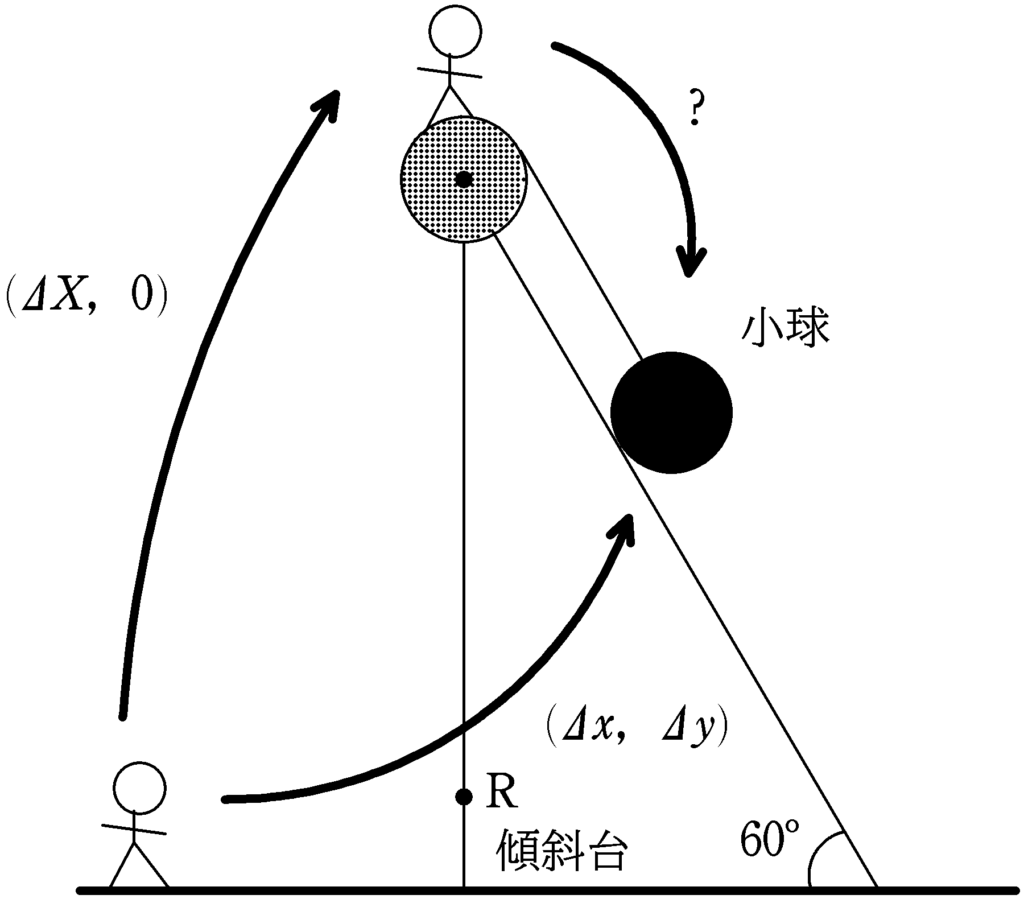
$(\varDelta X,0)+$傾斜台からみた小球の変位$=(\varDelta x,\varDelta y)$
傾斜台からいた小球の変位$=(\varDelta x,\varDelta y)-(\varDelta X,0)=(\varDelta x-\varDelta X,\varDelta y)$

いま,水平方向の変位は左方向を正としたけど,斜面を下っている方向を考えたいから,右方向の変位を計算しておきましょう.
右方向の変位は$-$をつけた,
$-(\varDelta x-\varDelta X)=\varDelta X-\varDelta x$
だね.
たとえば,左に$-3\,\rm m$移動したとき,右方向に$-(-3)=3\rm m$移動したともいえるよね.
傾斜台からみた小球は,斜面に平行な方向に変位するから次のようになります.


三角比を考えれば,
$\cos60^{\circ}=\dfrac{\varDelta X-\varDelta x}{2\varDelta X}$
$\varDelta x=0$ (答)
(2)

$\varDelta x=0$を考慮すると,傾斜台からみた小球の変位は次のようになるね.
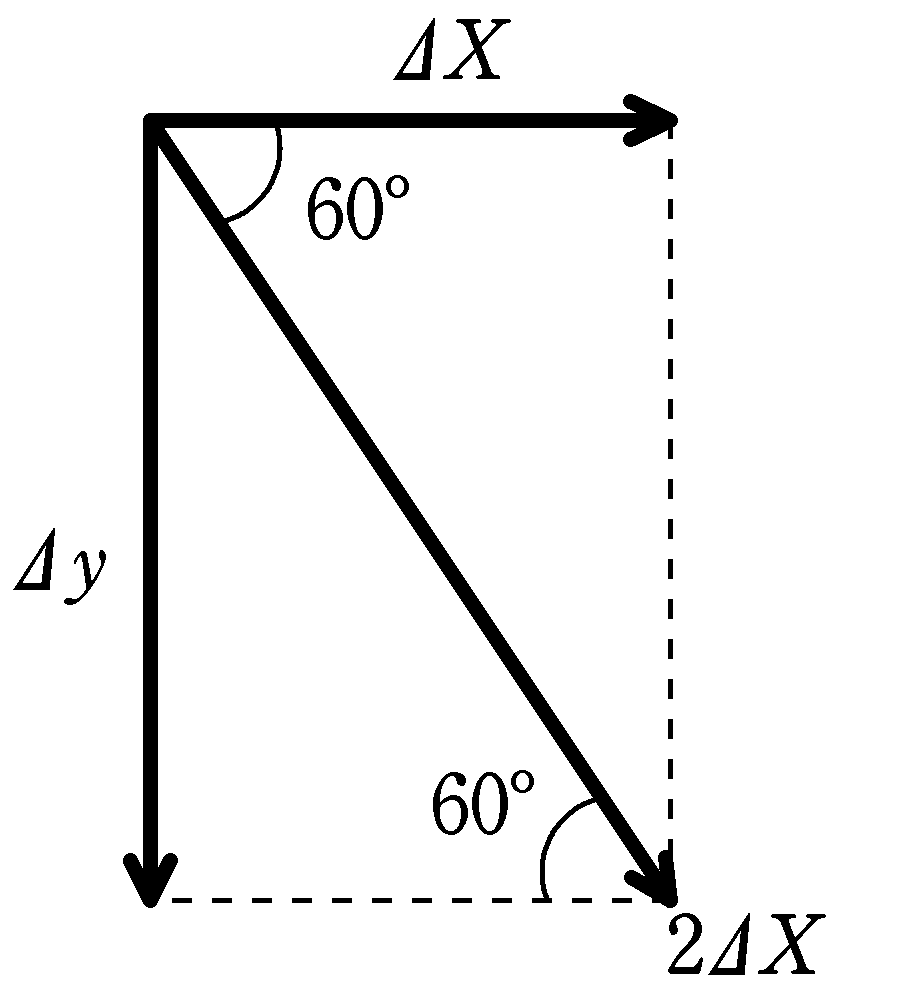

同様に,三角比を考えると
$\tan60^{\circ}=\dfrac{\varDelta y}{\varDelta X}$
$\therefore \varDelta y=\sqrt{3}\varDelta X \cdots (\ast)$ (答)
(3)

力を図示し,分解して,運動方程式を立てます.
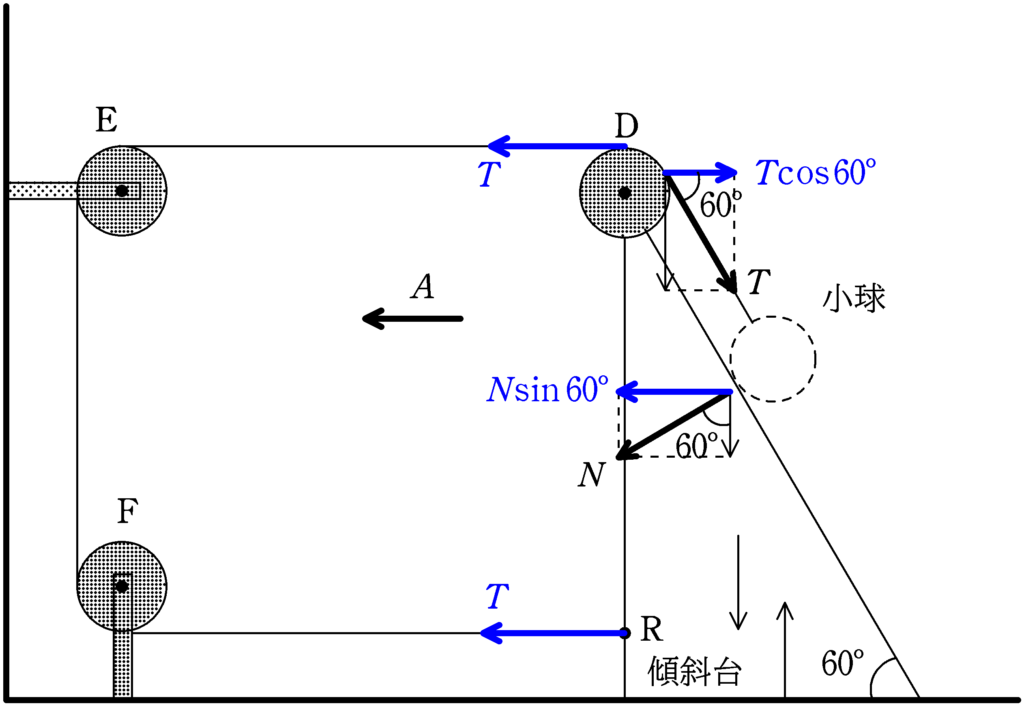
★ 傾斜台の運動方程式
$5mA=T+T+N\sin60^{\circ}-T\cos60^{\circ}$ $\cdots (2\ast)$ (答)
(4)

同じく小球にはたらく力を図示します.水平方向は(1)より変位$0$なので,加速度も$0$.
であることに注意しよう.
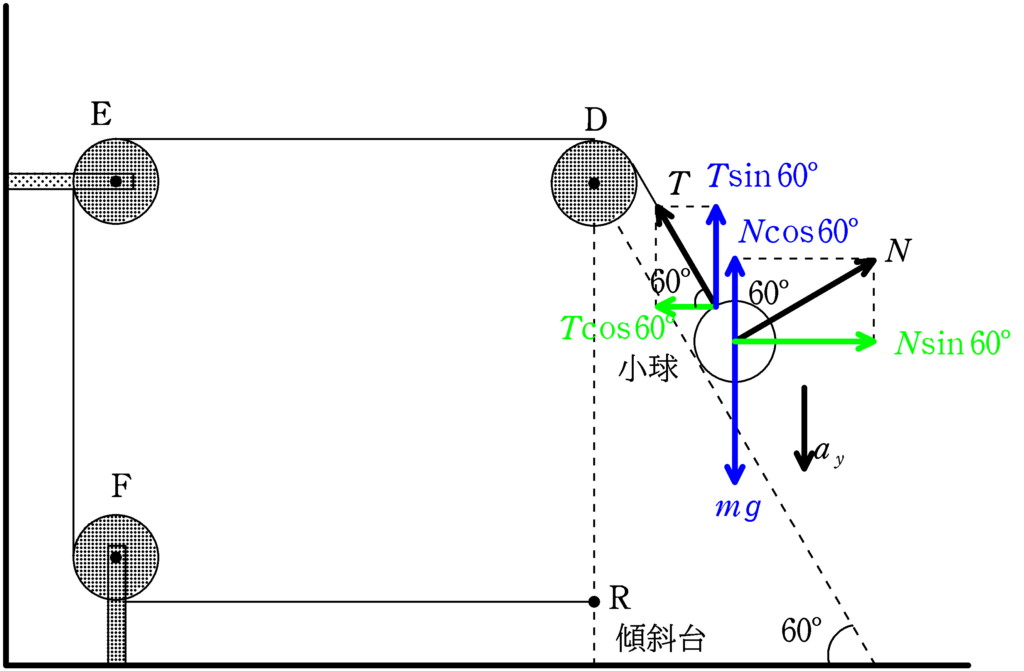
★ 水平方向の運動方程式
$m\times 0=T\cos60^{\circ}-N\sin60^{\circ}$ $\cdots (3\ast)$
★ 鉛直方向の運動方程式
$ma_{y}=mg-T\sin60^{\circ}-N\cos60^{\circ}$ $\cdots (4\ast)$ (答)
(5)

(2)で得た束縛条件$(\ast)$より,
$\varDelta y=\sqrt{3}\varDelta X$
なので,加速度の関係は
$a_{y}=\sqrt{3}A$ $\cdots (5\ast)$
となります.
いままで立てた運動方程式$(2\ast)$から$(4\ast)$も含めて書き出すと次のようになります.
(式は整理しておきます.)
$5mA=\dfrac{3}{2}T+\dfrac{\sqrt{3}}{2}N$ $\cdots (2\ast)$
$T=\sqrt{3}N$ $\cdots (3\ast)$
$ma_{y}=mg-\dfrac{\sqrt{3}}{2}T-\dfrac{1}{2}N$ $\cdots (4\ast)$
$a_{y}=\sqrt{3}A$ $\cdots (5\ast)$

これらの式から$A,a_{y},T,N$を求めましょう.
★ $(3\ast)$を$(2\ast)$と$(4\ast)$に,$(5\ast)$を$(4\ast)$に代入して$T$と$a_{y}$を消去
$(2\ast)$:$\eqalign{5mA&=\dfrac{3}{2}\times \sqrt{3}N+\dfrac{\sqrt{3}}{2}N\\&=2\sqrt{3}N}$
$(3\ast)$:$\eqalign{\sqrt{3}mA&=mg-\dfrac{\sqrt{3}}{2}\times \sqrt{3}N-\dfrac{1}{2}N\\&=mg-2N}$
★ 上式の$(3\ast)$の方の式より$2N=mg-\sqrt{3}mA \cdots (6\ast)$として,上式の$(2\ast)$の方の式に代入すると
$5mA=\sqrt{3}\times (mg-\sqrt{3}mA)$
$\therefore A=\dfrac{\sqrt{3}}{8}g$ (答) $\cdots (7\ast)$
★ $(7\ast)$を$(6\ast)$に代入して
$2N=mg-\sqrt{3}m\times \dfrac{\sqrt{3}}{8}g$
$\therefore N=\dfrac{5}{16}mg$ (答)
★ これを$(3\ast)$に代入して
$T=\dfrac{5\sqrt{3}}{16}mg$ (答)
★ $(7\ast)$を$(5\ast)$に代入して
$a_{y}=\sqrt{3}\times \dfrac{\sqrt{3}}{8}g=\dfrac{3}{8}g$ (答)


コメント