
次の問題は,2021年の東京理科大の問題の類題です.
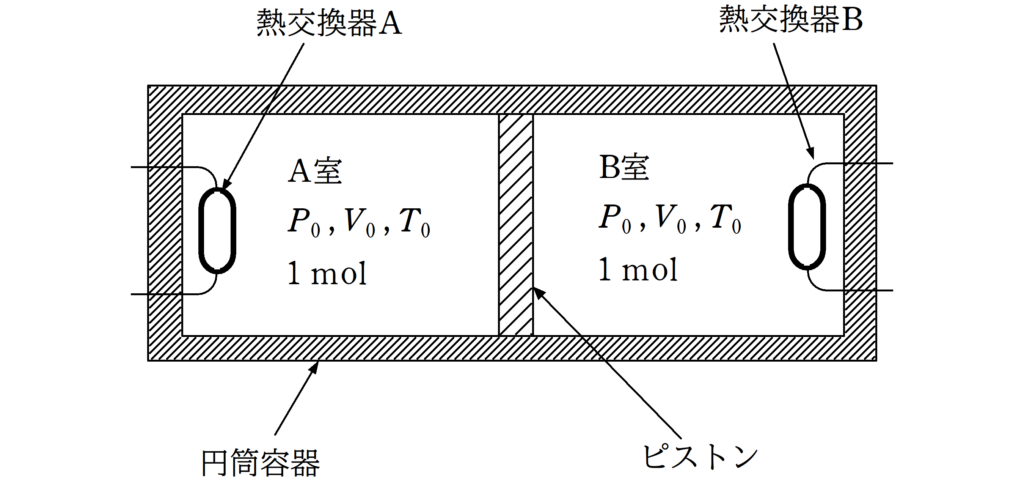
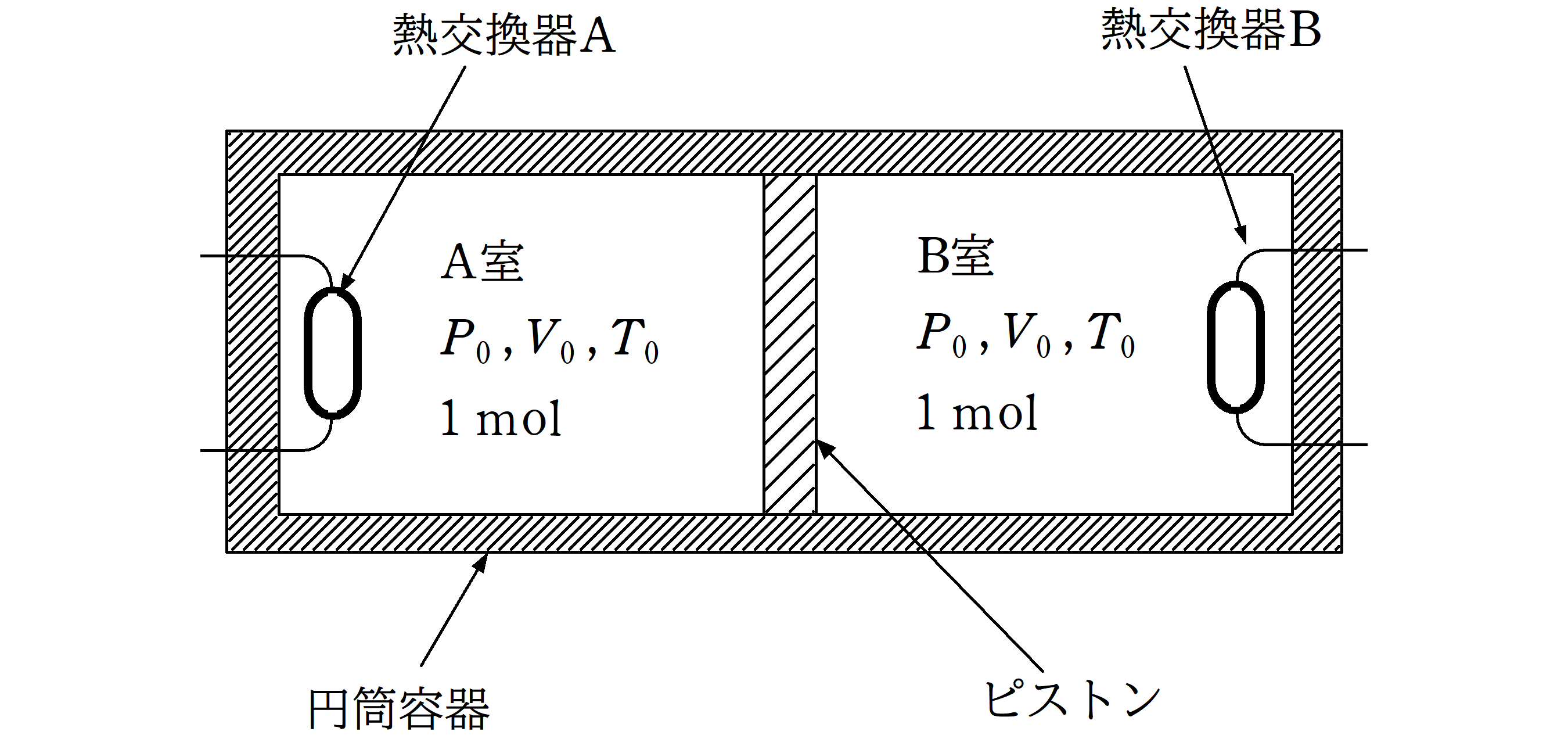
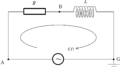
図に示すように,密閉された水平な円筒容器の中になめらかに動くピストンが入っており,ピストンによって容器内はA室とB室に分かれている.A室とB室にはそれぞれ熱交換器が設置されており,それぞれ熱交換器A,熱交換器Bとする.それぞれの熱交換器を作動させると,各室の気体に熱を加えたり,各室から熱を奪うことができる.円筒容器とピストンは断熱材でできていて,熱交換器の大きさは無視できるとする.
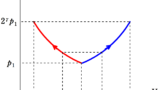
容器内のA室とB室には,それぞれ物質量$1\rm mol$の単原子分子理想気体が封入されている.A室とB室の気体の状態はともに,圧力$P_{0}$,体積$V_{0}$,絶対温度$T_{0}$である.この状態を初期状態という.初期状態から,次の過程1~3を経るまでのB室にある気体分子の圧力と体積の関係を図示したグラフとして最も適切なものを次の中から選べ.ただし,すべての状態変化は十分ゆっくり行われるものとする.
過程1
初期状態より,熱交換器Aは作動させないでおいて,熱交換器Bを作動させ,B室の気体の体積を$(1+\alpha)V_{0}$$(0<\alpha <1)$とする.この状態を状態1とする.
過程2
状態1より,熱交換器AとBを必要に応じて作動させ,A室の気体の温度を一定に保ちながら,B室気体の体積を$V_{0}$にもどす.この状態を状態2とする.
過程3
状態2より,熱交換器AとBをともに作動させ,A室とB室の気体の体積を$V_{0}$に保ちながら,初期状態にもどす.
<解答>

過程1から3において,B室の気体の状態変化ははっきりとわからないことばかりです.
しかし,A室の気体の状態変化ははっきりとわかります.
A室は
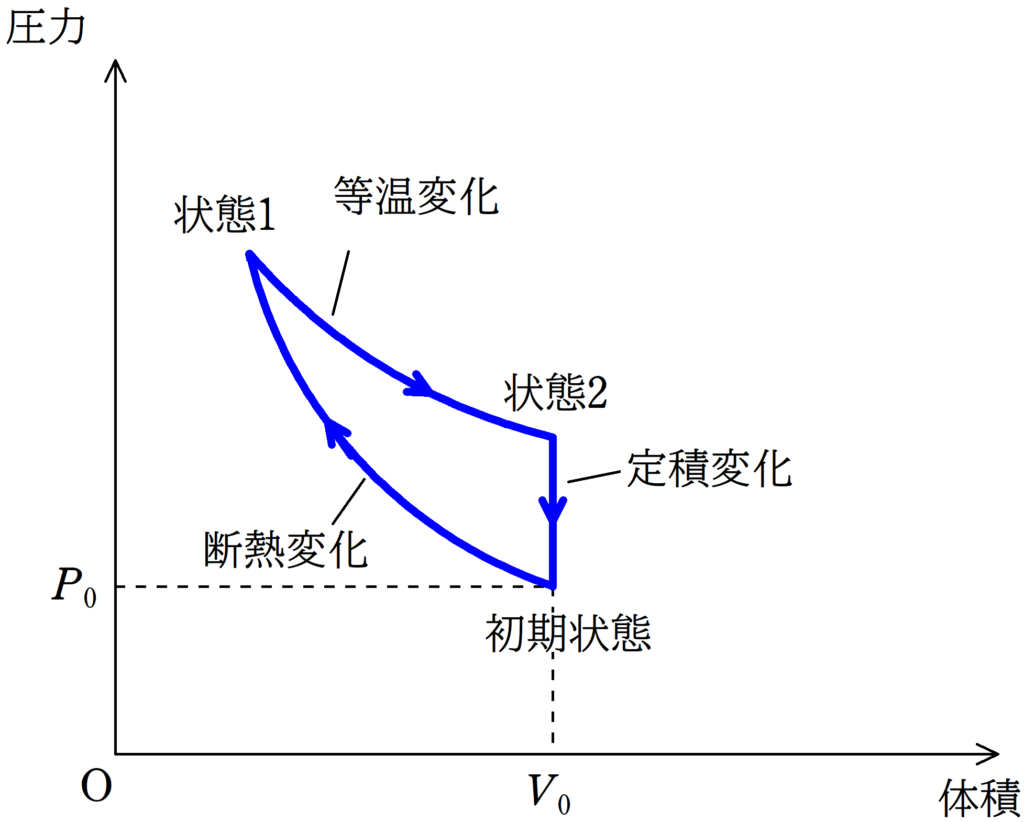
過程1→断熱変化
過程2→等温変化
過程3→定積変化
です.

断熱変化,等温変化の$pV$図については,下の記事でも説明しているよ.
断熱変化は等温変化より傾きが急なんだよね.

A室の気体の$pV$図は次のようになります.

では,B室の気体はどのように変化するのでしょうか?
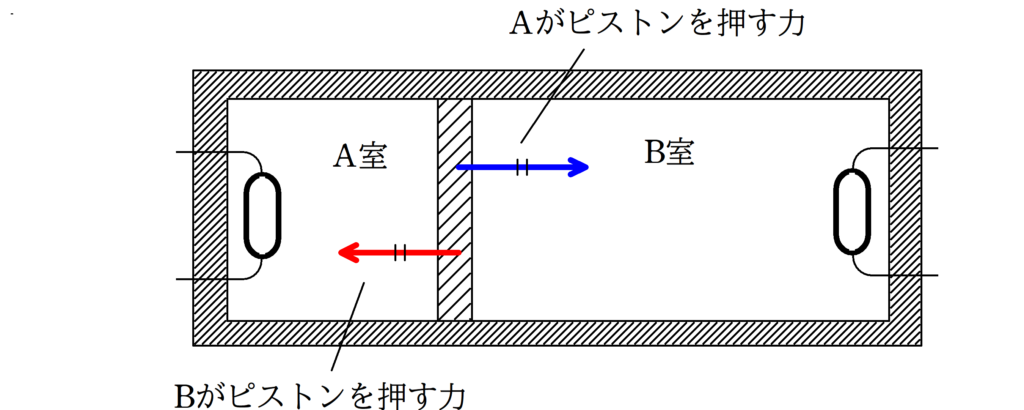
これは,A室とB室の気体の圧力が常に等しいことを利用しましょう.

ピストンはつねにつりあっています.
ピストンにはたらく水平方向の力はA室とB室の気体の力しかないので,圧力が等しくなるんだね.

すると,A室の気体の$pV$図のグラフを利用してB室の気体の$pV$図をかくことができます.
下図は,A室が断熱変化するときのグラフです.
A室の体積が減った分,B室の体積が増えることと,A室とB室の気体の圧力が常に同じであることを利用しています.
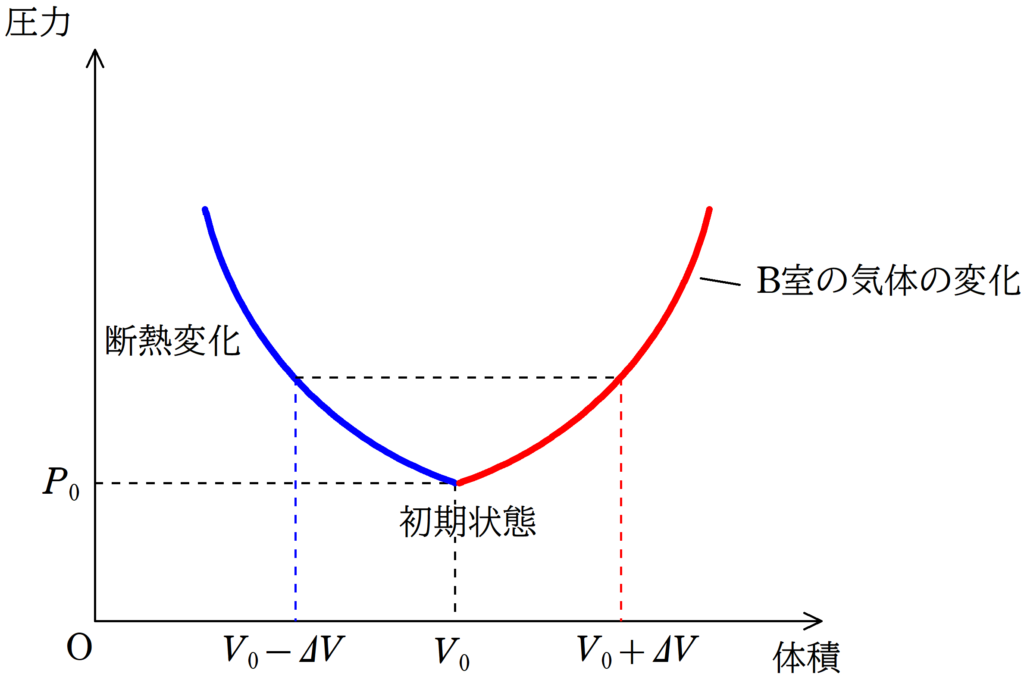

他の過程についても考えると,次のようになるね.
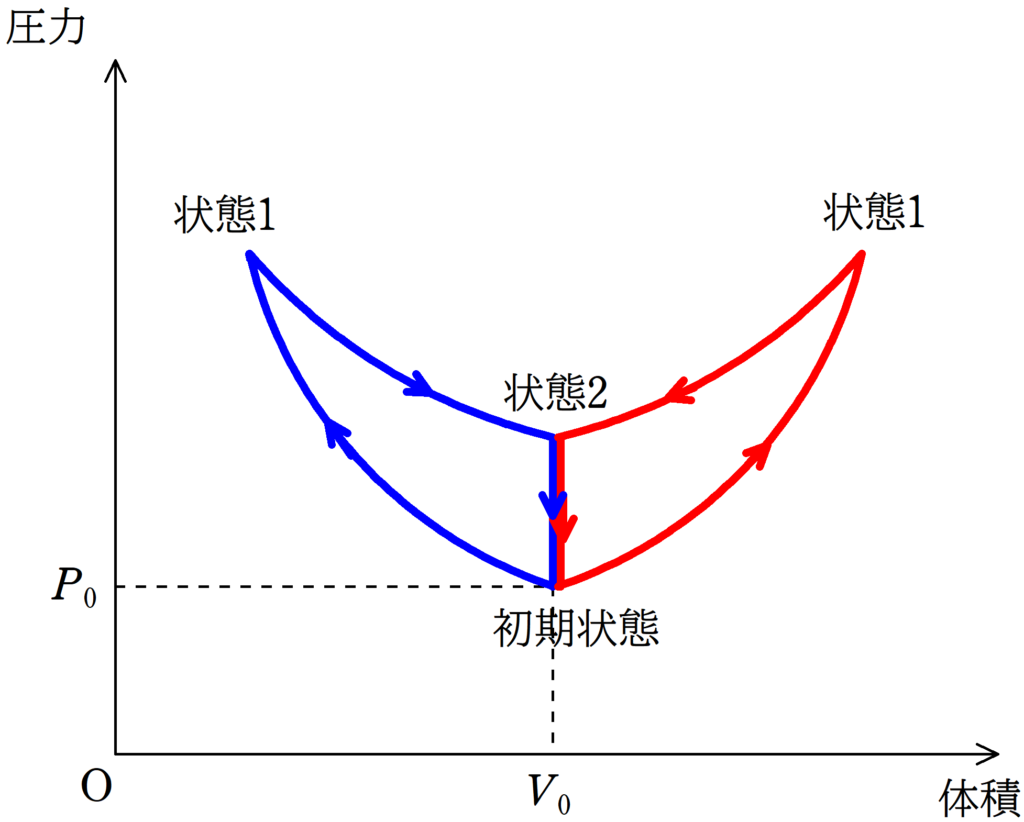

上図のグラフの赤い方の曲線がB室の$pV$図です.
したがって,適するグラフは③(答)となります.

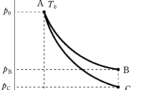
類題として次の問題も解いてみてください!

コメント
[…] 片側の$pV図$がわかっているときのもう片方の$pV$図NEKO次の問題は,2021年の… 分野別 演習問題 熱力学 高校物理 シェアする Twitter Facebook はてブ LINE physicmathをフォローする physicmath Physicmath(フィジクマス) […]