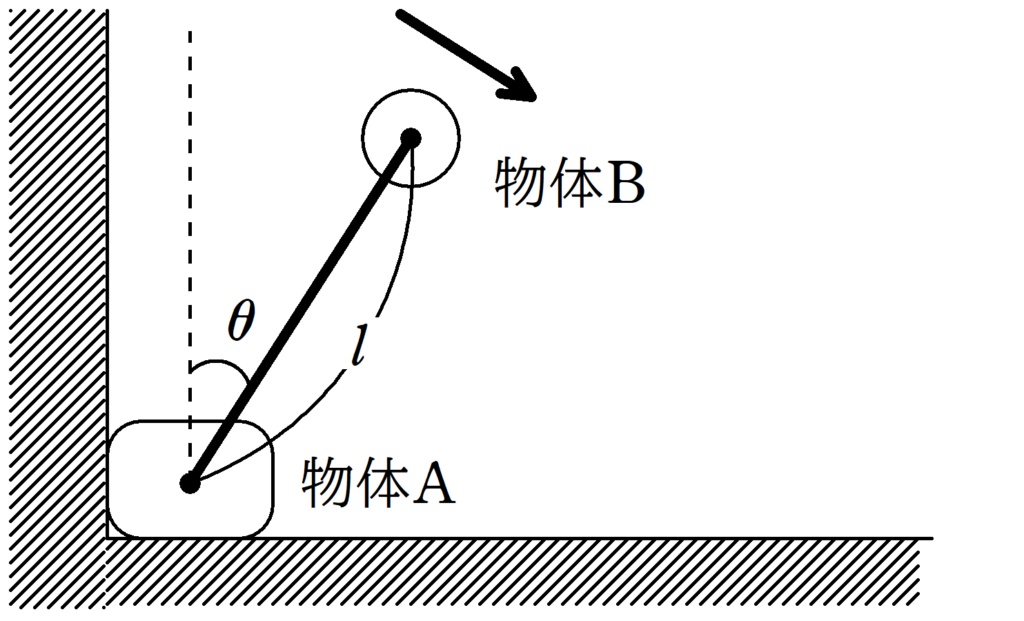
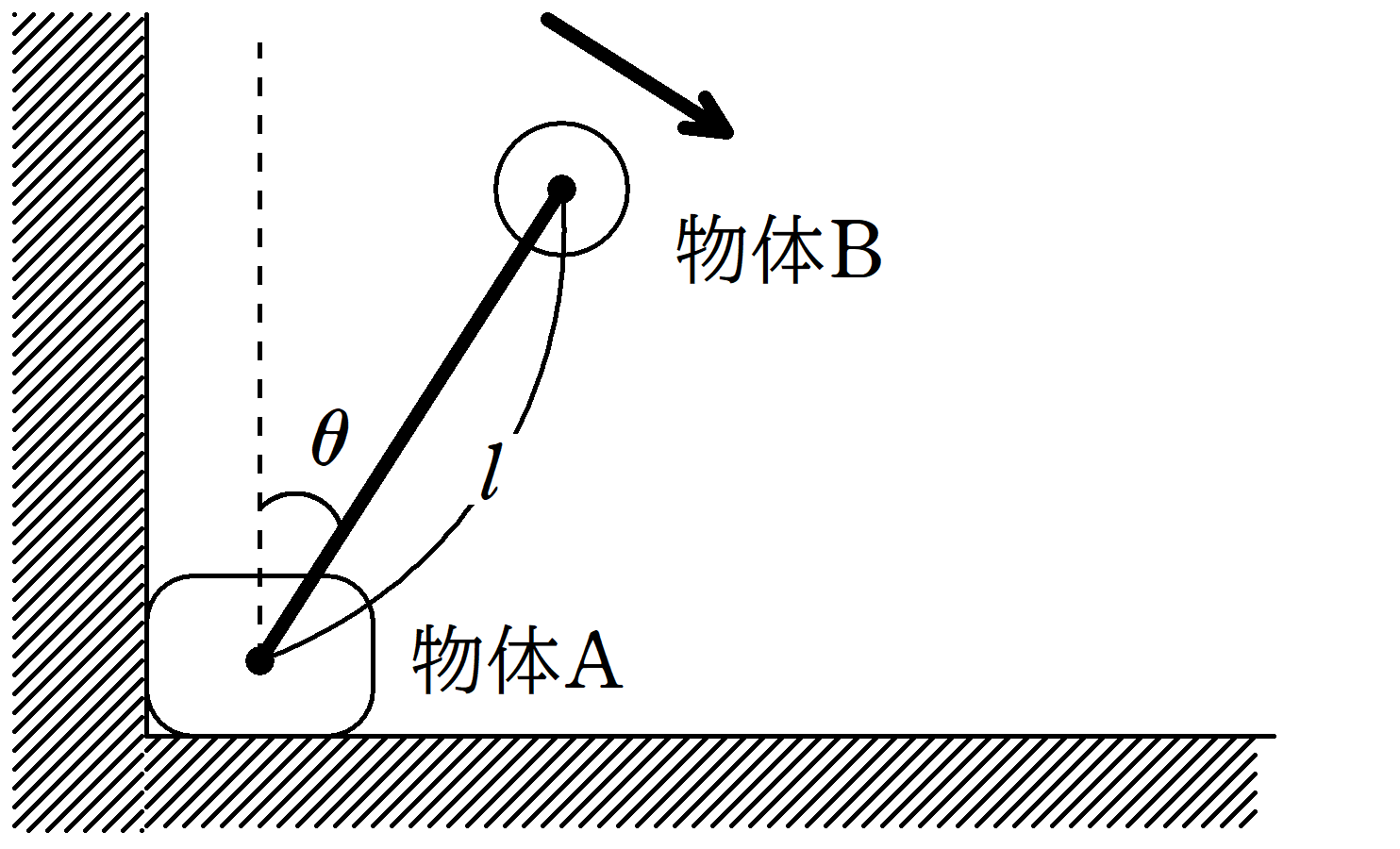
図のように,長さ$l$で質量の無視できる棒によってつながれた,質量$M$の物体$\rm A$と質量$m$の物体$\rm B$の運動を考える.ただし,$M>m$とする.棒は物体$\rm A$および物体$\rm B$に対してなめらかなに回転でき,棒が鉛直方向となす角を$\theta$とする.はじめ,物体$\rm A$は水平な床の上で鉛直な壁と接していた.一方,物体$\rm B$は物体$\rm A$の真上$(\theta=0^{\circ})$から初速度$0$で右側へ動きはじめた.その後の運動について,次の問いに答えよ.なお,重力加速度の大きさを$g$として,物体$\rm A$と物体$\rm B$の大きさは考えなくてよい.また,物体$\rm A$および物体$\rm B$との間にはたらく力は棒に平行である.
物体$\rm A$と床との間に摩擦がないとする.
(1) 物体$\rm B$が動きだしてからしばらくの間は,物体$\rm A$は壁に接したままであった.この間の物体$\rm B$の速さ$v$を$\theta$を含んだ式で表せ.
(2) (1)のとき,棒から物体$\rm B$にはたらく力$F$を,$\theta$を含んだ式で表せ.棒が物体$\rm B$を押す向きを正とする.
(3) $\theta=\alpha$において,物体$\rm A$から壁から離れて床の上をすべりはじめた.$\cos\alpha$を求めよ.
(4) $\theta=\alpha$における物体$\rm B$の運動量の水平成分$P$を求めよ.
(5) 物体$\rm B$が物体$\rm A$の真横$(\theta=90^{\circ})$にきたときの,物体$\rm A$の速さ$V$を$P$を含んだ式で表せ.
<解答>
(1)
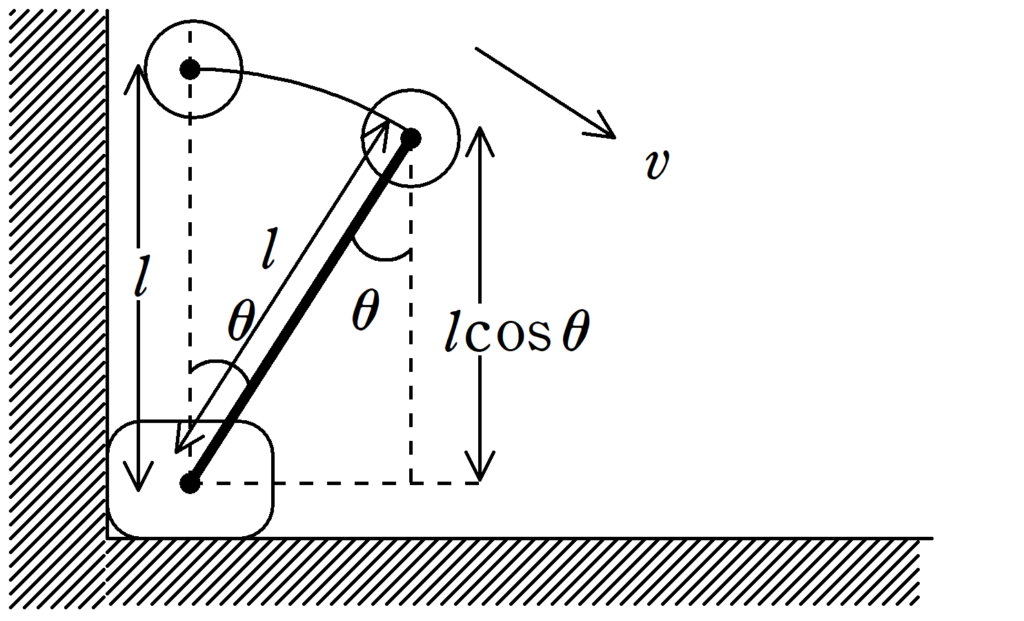

水平面を重力による位置エネルギーを基準として力学的エネルギー保存則を立てましょう.
★ 力学的エネルギー保存則
$\eqalign{\dfrac{1}{2}mv^{2}+mgl\cos\theta&=\dfrac{1}{2}m\cdot 0^{2}+mgl\cr \dfrac{1}{2}mv^{2}&=mgl(1-\cos\theta)}$
$\therefore v=\sqrt{2gl(1-\cos\theta)}$ (答)
(2)
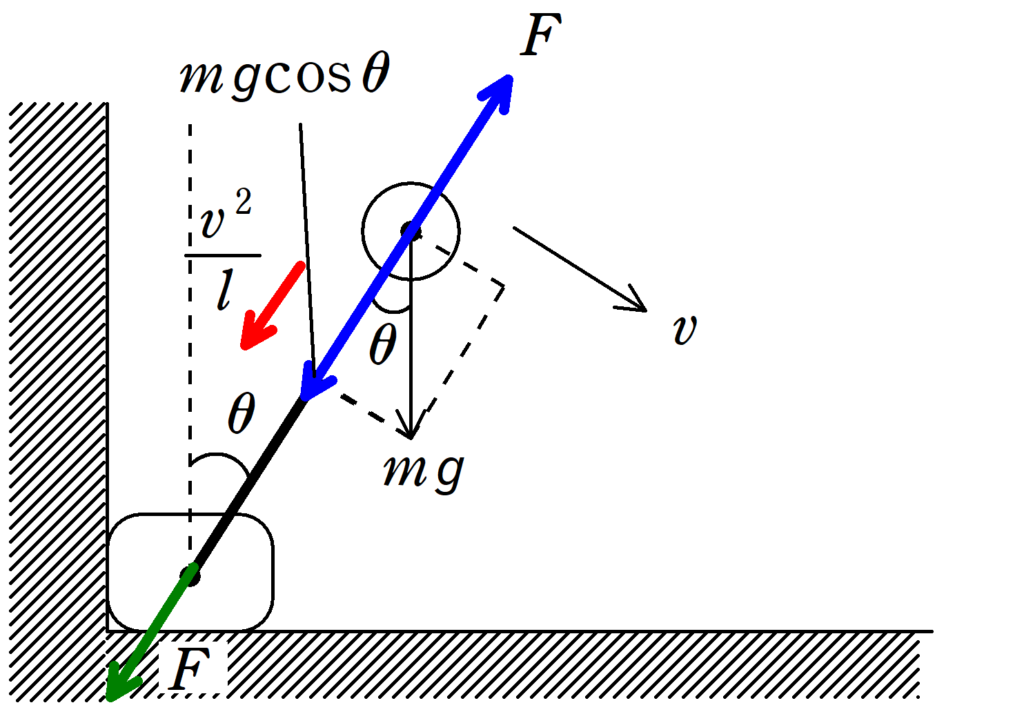

$\rm B$は円運動しているので,円運動の運動方程式を立てて力$F$を求めます.重力$mg$の向心方向成分は上図のように,$mg\cos\theta$です.
半径$r$,円運動の接線方向の速さを$v$,角速度を$\omega$とすると,向心加速度の大きさ$a$は
$a=\dfrac{v^{2}}{r}=r\omega^{2}$
向心加速度の向きは円運動の中心
★ $\rm B$の向心方向の運動方程式
$m\dfrac{v^{2}}{l}=mg\cos\theta-F$
(1)の$v=\sqrt{2gl(1-\cos\theta)}$より,
$\eqalign{F&=mg\cos\theta-m\dfrac{v^{2}}{l}\\&=mg\cos\theta-m\dfrac{1}{l}\{2gl(1-\cos\theta)\}\\&=(3\cos\theta-2)mg}$
したがって,$F=(3\cos\theta-2)mg$(答)
(3)
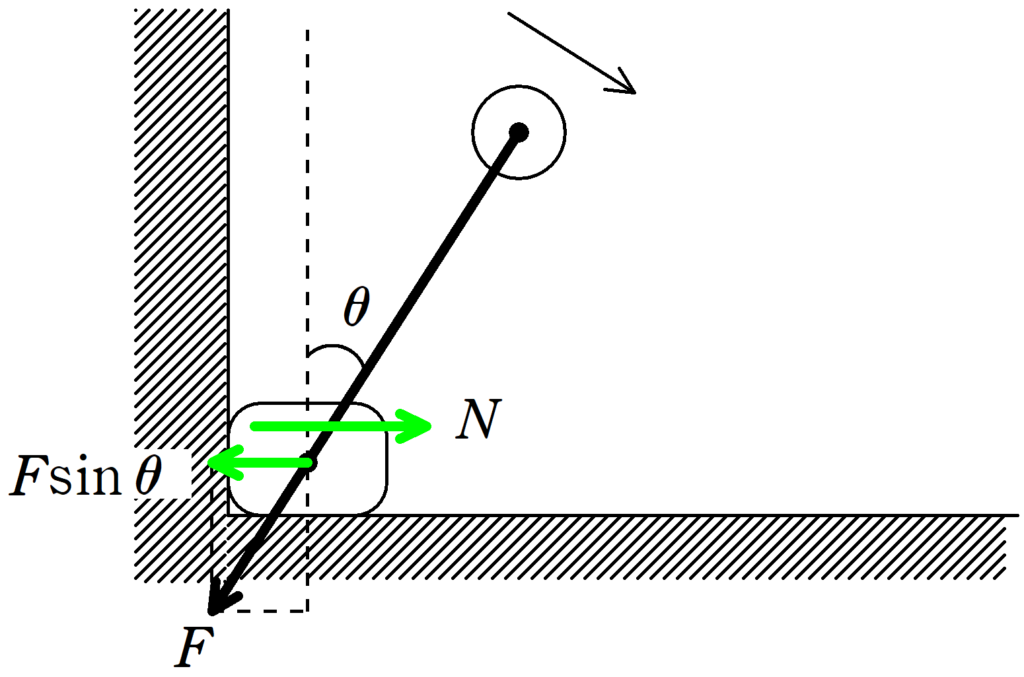

上図のように物体$\rm A$にはたらく水平方向の力を考えます.
このとき,壁が物体$\rm A$を押す力を$N$としたとき,$N=0$で物体$\rm A$が壁から離れます.
★ 物体$\rm A$の水平方向のつり合い($N=0$のとき)
$F\sin\theta=0$
(2)より,$F=(3\cos\theta-2)mg$なので,$F=0$である条件は,$\cos\alpha=\dfrac{2}{3}$(答)のとき.
(4)

$\cos\theta=\dfrac{2}{3}$のとき,
$\eqalign{v&=\sqrt{2gl(1-\cos\theta)}\\&=\sqrt{\dfrac{2}{3}gl}}$
です.
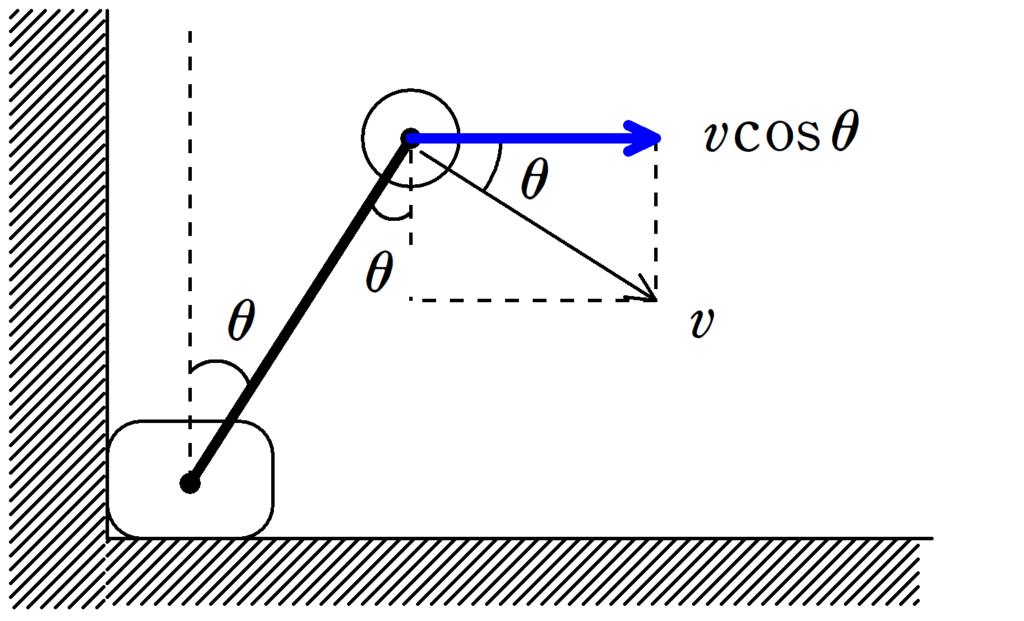
$\cos\theta=\dfrac{2}{3}$のときの水平方向の運動量の大きさ$P$は,上図より
$\eqalign{P&=mv\cos\theta\\&=m\sqrt{\dfrac{2}{3}gl}\cdot \dfrac{2}{3}}$
したがって,$P=\dfrac{2}{3}m\sqrt{\dfrac{2}{3}gl}$ (答)
(5)

運動量保存則を立てます.
★ 運動量保存則
$P=(M+m)V$
$\therefore V=\dfrac{P}{M+m}$ (答)


コメント