
前回までで,初期条件から座標の式を求める練習と,運動方程式から中心座標や角振動数,周期を求める練習をしました.今回は,いよいよ運動方程式を立てていきます.運動方程式は以下のステップで立てましょう.
- 運動方程式を立てる対象物体と座標を決める.
- 座標の+の向きに加速度$a$を設定して,位置$x$における対象物体にはたらく力を図示する.
- 必要であれば,力を分解し運動方程式を立てる.

注意事項です.1.の座標は原点と+の向きを決定することになりますが,原点はバネの自然になる位置やつり合いの位置,一番端などの特別な場所がいいでしょう.また,座標を決めるということはその座標が止まっているか,動いているかも決めるということです.ここらへんは忘れやすいところなので,座標が動く場合は少し意識してかく癖をつけた方がよいでしょう.さらに,2.で立てる位置$x$は自然長の位置や,原点,つり合いの位置,はじめの位置などの特別な位置ではなく,一般的な位置で立てましょう.
それでは,問題を解いてみましょう.

上図のように質量$m$の物体が水平でなめらかな床の上に静止している.ばね定数$k$のばねの一端を物体にとりつけ,他端は壁に固定する.いま,ばねが自然長になる位置を原点として,ばねが伸びる方向に$x$軸をとる.物体に力を加えて,自然長から$A$だけ伸びた状態で静かに手をはなしたところ,物体は単振動をした.次の問いに答えよ.
(1) 物体が位置$x$にあるときの加速度を$a$として,物体の運動方程式を立てよ.
(2) (1)の運動方程式より,振動の中心座標$x_{0}$,角振動数$\omega$,振動の周期$T$を$k$,$m$から必要なものを用いて表せ.
(3) 位置$x=A$より手をはなした時刻を$t=0$としたとき,位置$x$の時間変化を$A$,$m$,$k$,$t$を用いて表せ.
<解答>
今回は,座標や加速度をあらかじめて設定しています.
(1) 位置$x$における水平方向にはたらく力は弾性力だけです.弾性力は自然長にもどる方向に,(ばね定数)×(自然長からの距離)だけ力がはたらきます.
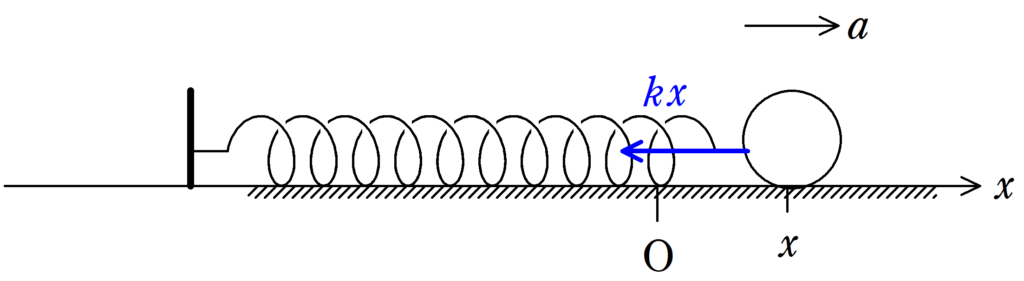
$x>0$であれば,上図のような向きに弾性力がはたらきますね.運動方程式は
$ma=-kx$
です.それでは,$x<0$ではどうでしょうか.
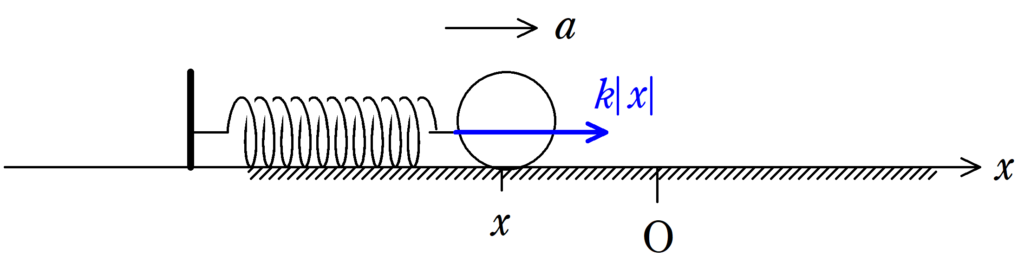
右向きにはたらくから$ma=kx$ではありません!弾性力の大きさは$k|x|$です.$x<0$なので,$|x|=-x$ですね.だから$x<0$のときの運動方程式は下のようになります.
$ma=k|x|=-kx$
つまり,$x>0$でも$x<0$でも運動方程式は同じ形になるのです.答.$ma=-kx$
(2) 運動方程式から,中心座標$x_{0}=0$,角振動数$\omega=\sqrt{\dfrac{k}{m}}$,周期$T=2\pi\sqrt{\dfrac{m}{k}}$となります.
(3) $x=A$で静かに手をはなすと$x=A$からスタートして$x$軸の負の方向にいくので,$\cos$型ですね.振動の中心が$x=0$で,振動の右端が$x=A$なので,振幅(中心から端までの距離)は$A$となります.下図のような振動をします.答えは$x=A\cos \omega t=A\cos \sqrt{\dfrac{k}{m}}t$です.
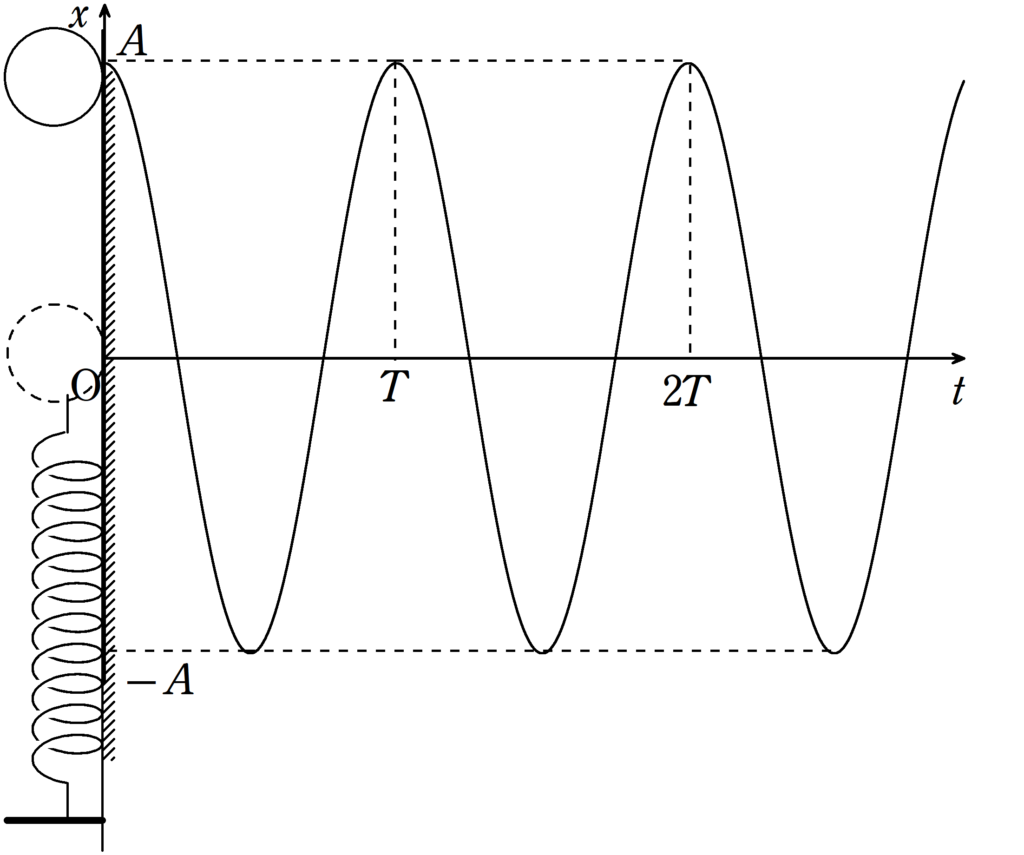

だんだんと実践的な問題になってきました.単振動の問題は
- 運動方程式を立てる
- 運動方程式から振動の中心と角振動数,周期を読み取る
- 初期条件から$x$の時間変化を求める
これから少しずつ難易度があがっていきます.この一連の流れを確認しておきましょう.
次回はこちら





コメント
[…] [基本]単振動の演習問題⑤ 運動方程式を立てる1 の続きです. […]
[…] 次の問題はこちら […]
[…] [基本]単振動の演習問題⑤ 運動方程式を立てる1NEKO前回までで,初期条件… […]