ベータトロン軌道内の磁束密度の変化と軌道上の磁束密度の変化

NEKO

ベータトロンの問題では，2つの磁束密度が登場するよね？

なんで2つの磁束密度が出てくるんだろう？

PHYさん

ベータトロンは荷電粒子の加速器の一種です．

ベータトロンは荷電粒子の軌道半径を一定に保ったまま加速します．

荷電粒子を加速するための磁束密度と荷電粒子の軌道半径を一定にするための磁束密度が異なるんです．

PHYさん

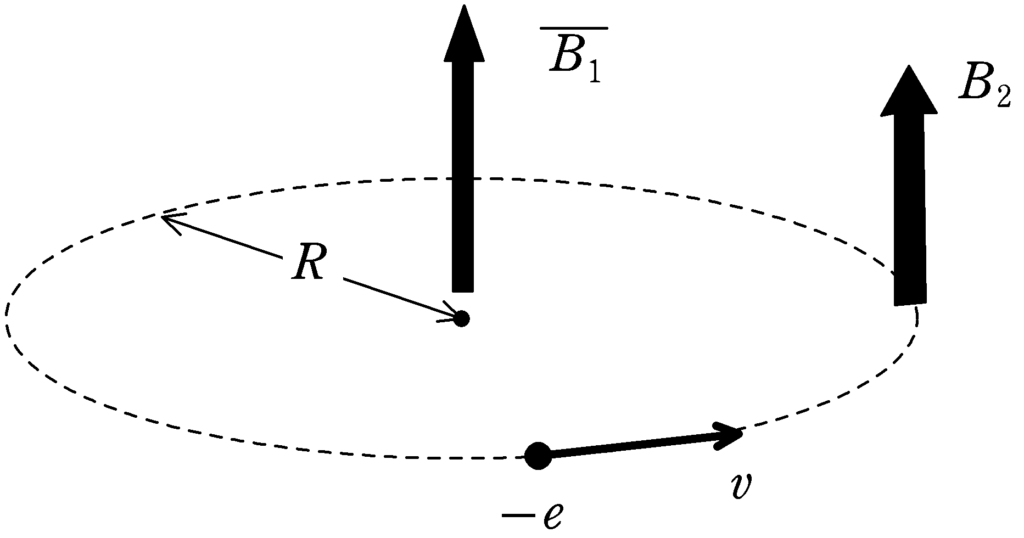
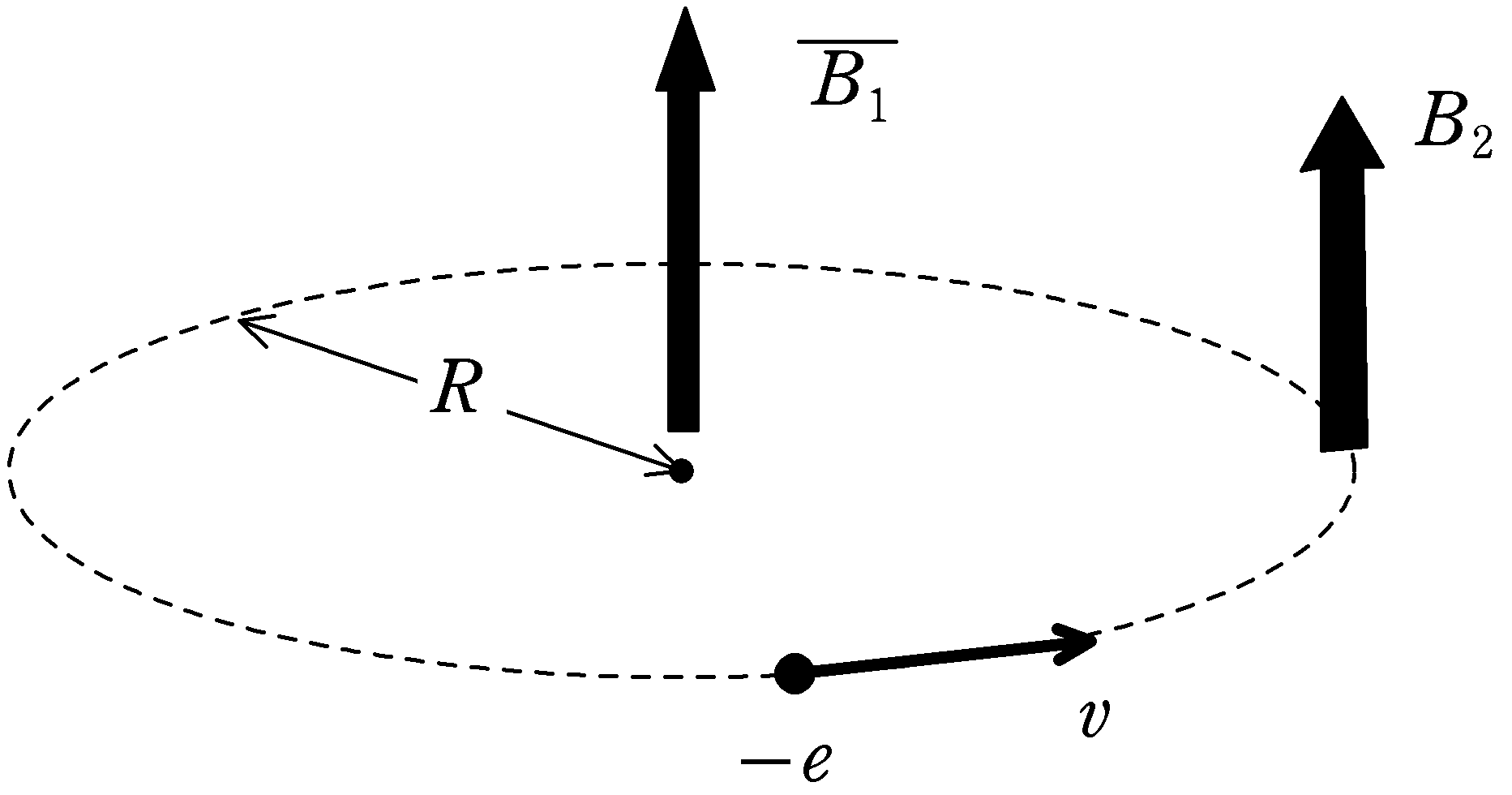
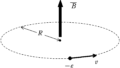
上図は，電子が半径$R$の軌道で加速されている様子です．

軌道内部の平均磁束密度$\overline{B_{1}}$を変化させることで電子を加速し，軌道上の磁束密度$B_{2}$を変化させることで軌道半径を維持させます．

電子を加速する
電子の軌道を保つ
ベータトロン条件

電子を加速する

ファラデーの電磁誘導の法則

$\varDelta t$の間に磁束が$\varDelta \varPhi$変化するときに生じる誘導起電力の大きさ$V$は

$V=|\dfrac{\varDelta \varPhi}{\varDelta t}|$

$\varPhi$と$B$の関係

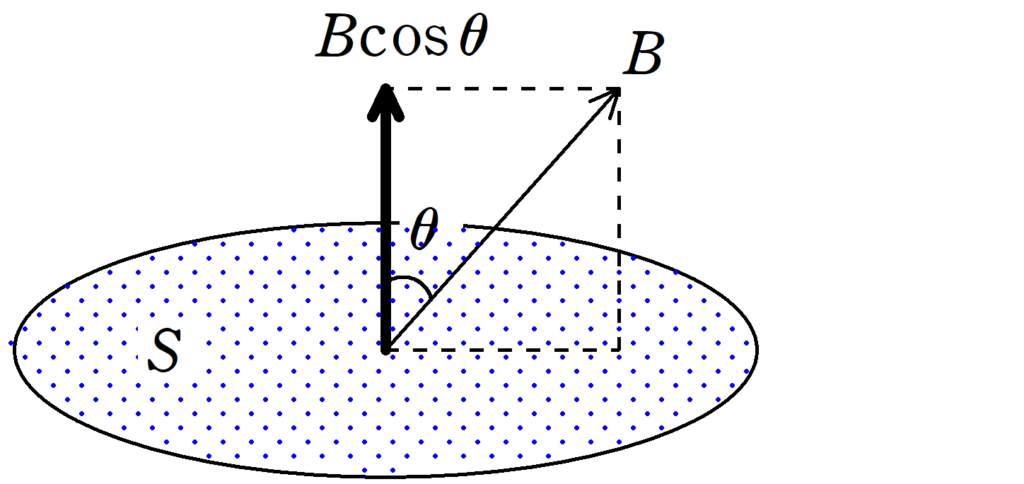
上図のように，面積$S[\rm m^{2}]$の部分を磁束密度の大きさ$B[\rm Wb/m^{2}]$の磁場が面に垂直な線に対して$\theta$の方向にかかっているとき，この面を貫く磁束$\varPhi$は

$\eqalign{\varPhi&=(B\cos\theta)S\\&=BS\cos\theta}$

となる．

NEKO

軌道内部の平均磁束密度を時間$\varDelta t$で$\varDelta \overline{B_{1}}$だけ変化すると，生じる誘導起電力の大きさ$V$は，次のようになります．

$\eqalign{V&=\dfrac{\varDelta \overline{B_{1}}\cdot \pi R^{2}}{\varDelta t}\\&=\pi R^{2}\dfrac{\varDelta \overline{B_{1}}}{\varDelta t}}$

PHYさん

次の，電場と電位差の関係より，円軌道上に生じる電場（誘導電場）の大きさを計算しましょう．

円軌道の周の長さは$2\pi R$ですね．

電場の電位差の関係

電場の大きさを$E$，距離$\Delta x$の電位差を$\Delta V$とするとき，次の関係が成り立つ．

$E=\left|\dfrac{\Delta V}{\Delta x}\right|$

$\eqalign{E&=\dfrac{\cancel{\pi} R^{\cancel{2}}\dfrac{\varDelta \overline{B_{1}}}{\varDelta t}}{2\cancel{\pi} \cancel{R}}\\&=\dfrac{R}{2}\dfrac{\varDelta \overline{B_{1}}}{\varDelta t}}$

PHYさん

この電場によって電子が軌道の方向に加速されます．

このときのクーロン力の大きさ$F$は，次のようになります．

$F=eE=\dfrac{eR}{2}\dfrac{\varDelta \overline{B_{1}}}{\varDelta t}$

$\therefore F\varDelta t=\dfrac{eR\varDelta \overline{B_{1}}}{2}$

NEKO

電子は力積(力×時間)を受けているので，電子の運動量の大きさが変化するね．

電子の質量を$m$，速さの変化を$\varDelta v$とすると

$\eqalign{m\varDelta v&=F\varDelta t\\&=\dfrac{eR\varDelta \overline{B_{1}}}{2}}$

$\therefore \varDelta v=\dfrac{eR\varDelta \overline{B_{1}}}{2m}$ $\dots (\ast)$

PHYさん

このように，軌道内部の磁束密度の変化によって，電子が加速されます．

電子の軌道を保つ

PHYさん

軌道上の磁束密度の大きさを$B_{2}$としましょう．

磁場中を荷電粒子が速度をもっているとローレンツ力を受けて，円運動します．

ローレンツ力

磁場の大きさを$B$，磁場に垂直な速度の大きさを$v$，荷電粒子の電荷を$q$のとき，荷電粒子が受けるローレンツ力の大きさ$f$は

$f=|q|vB$

向きはフレミング左手の法則に従う．

$\clubsuit$フレミング左手の法則$\clubsuit$

　親指→ローレンツ力の向き

　人差し指→磁場の向き

　中指→電流の向き（正電荷の動く向き，負電荷の動く向きと逆）

★　速さ$v$，半径$R$の等速円運動の向心方向の運動方程式

$m\dfrac{v^{\cancel{2}}}{R}=e\cancel{v}B_{2}$

$\therefore v=\dfrac{eRB_{2}}{m}$　$\dots (2\ast)$

PHYさん

電子の速さが$v$から$v+\varDelta v$に変化したとき，円軌道の半径$R$を維持するために$B_{2}$を$B_{2}+\varDelta B_{2}$に変化させたとしましょう．

このときの運動方程式は次のようになります．

★　速さ$v+\varDelta v$，半径$R$の等速円運動の向心方向の運動方程式

$m\dfrac{(v+\varDelta v)^{\cancel{2}}}{R}=e\cancel{(v+\varDelta v)}(B_{2}+\varDelta B_{2})$

$\therefore v+\varDelta v=\dfrac{eR(B_{2}+\varDelta B_{2})}{m}$　$\dots (3\ast)$

NEKO

$(3\ast)-(2\ast)$を計算すると

$\varDelta v=\dfrac{eR\varDelta B_{2}}{m}$　$\dots (4\ast)$

となります．

ベータトロン条件

$$PHYさん

$(\ast)$より

$\varDelta v=\dfrac{eR\varDelta \overline{B_{1}}}{2m}$

$(4\ast)$より

$\varDelta v=\dfrac{eR\varDelta B_{2}}{m}$

です．これは同じ$\varDelta v$なので，$\varDelta \overline{B_{1}}$と$\varDelta B_{2}$には次の関係が成り立ちます．

$\dfrac{\cancel{eR}\varDelta \overline{B_{1}}}{2\cancel{m}}=\dfrac{\cancel{eR}\varDelta B_{2}}{\cancel{m}}$

$\varDelta \overline{B_{1}}=2\varDelta B_{2}$

PHYさん

このように，電子を半径を一定に保ちながら加速させるためには，軌道内部の平均磁束密度の変化と軌道上の磁束密度変化を$2:1$に保つ必要があります．

ベータトロン　軌道内の磁束密度の変化と軌道上の磁束密度の変化

電子を加速する

電子の軌道を保つ

ベータトロン条件

コメント