
中空導体球について,次のことが言えるみたいなんだけど,イマイチよくわからないなあ.
- 中空導体球内部に電荷がないとき,外部より電場をかけられても導体内側表面には電荷は分布せず,中空部分に電場が生じない.
- 中空導体球内部に電荷$Q$がある場合,導体内側表面に$-Q$の電荷が分布し,外側には$+Q$の電荷が分布する.内部の電荷を移動させると,導体内側表面の電荷の分布は変化するが,電荷の和は$-Q$である.そして,外側の電荷分布は変わらず,中空導体球の外側の電場は変化しない.
※ただし,「2.」において,中空導体球に蓄えられている電荷は$0$と考えた.
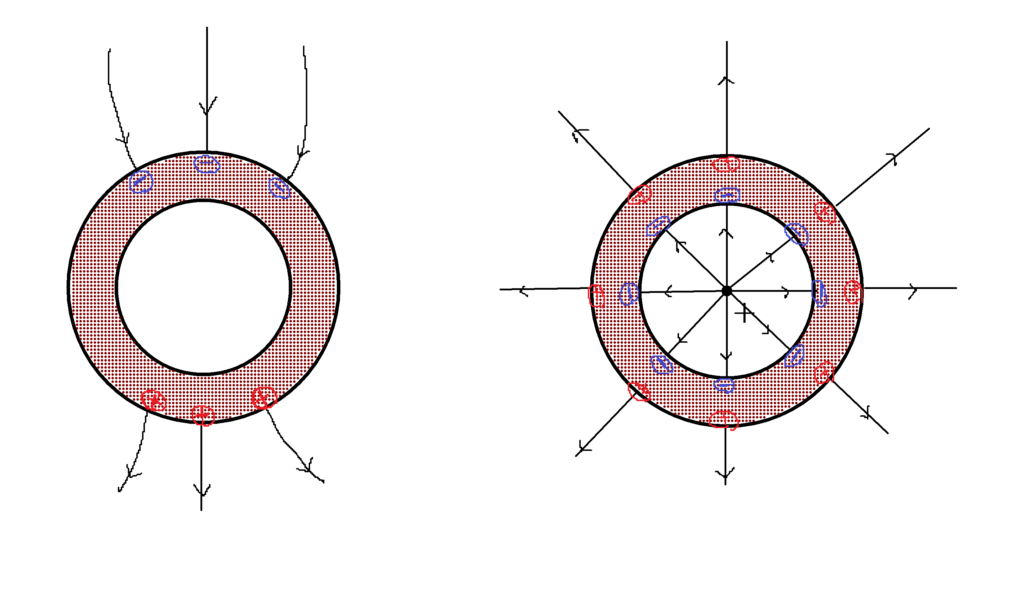

確かに静電遮蔽は直観的にわかりにくいところですね.
1つ1つ説明していきましょう.
中空導体球内部に電荷がないとき,外部より電場をかけられても導体内側表面には電荷は分布せず,中空部分に電場が生じない.

外部から電場がかけられたときに中空導体球の中空部分の電場が$0$というのは聞いたことがあるけど,内側部分の電荷も$0$なんだ.

そうなんです.
これを示すために,敢えて中空導体内側に電荷が蓄えられたとして考えてみましょう.
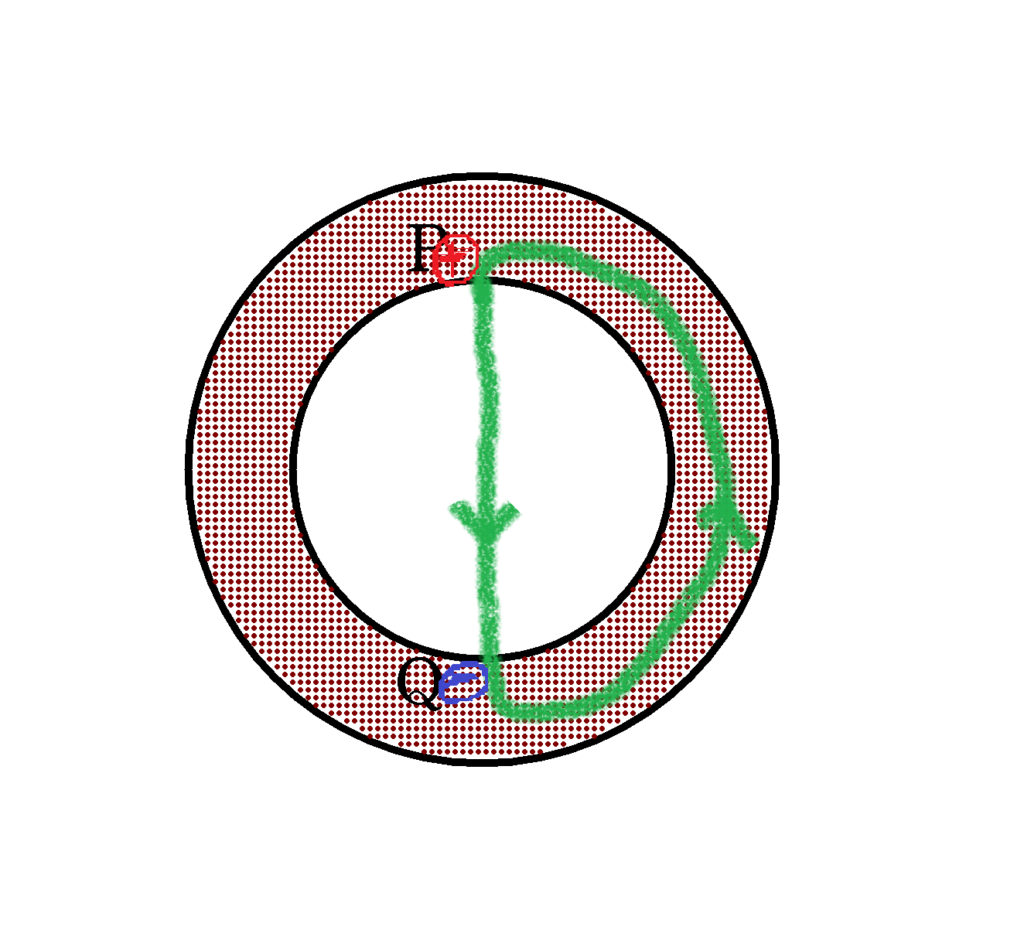
下図のように,Pに正の電荷が,Qに負の電荷が蓄えられているとしましょう.
Pをスタートして,Qを通り下図の緑色の経路をたどって電位を調べていきたいと思います.
このとき,導体内部の電場は$0$であることは前提としておいてください.もし,導体内部の電場が$0$でなければ,電位差が生じていることになり,電位が高い方から低い方へ電流が流れてしまいます.
電場の大きさを$E$,距離$\Delta x$の電位差を$\Delta V$とするとき,次の関係が成り立つ.
$E=\left|\dfrac{\Delta V}{\Delta x}\right|$

Pからスタートし,Qを経由して再びPへ戻ってくるので最終的には電位は同じになりますね.
Pの電位を$V_{\rm P}$,PからQの間の電位差を$\varDelta V$とすると次のような電位を追う式を書くことができます.
★Pからはじまり,Qを経由しPに戻る電位の式
$V_{\rm P}-\varDelta V-0=V_{\rm P}$
$\varDelta V=0$

PQ間の電位差がないってことは電場が$0$ってことだね.
電場が$0$ってことは,PとQそれぞれにある電荷がともに$0$であることになるね.

このように,中空導体球(いまの話からわかるように,導体の形には依りません.)の外部から電場をかけた場合,導体内側部分には電荷は分布せず,中空部分には電場が生じません.
中空導体球内部に電荷$Q$がある場合,導体内側表面に$-Q$の電荷が分布し,外側には$+Q$の電荷が分布する.内部の電荷を移動させると,導体内側表面の電荷の分布は変化するが,電荷の和は$-Q$である.そして,外側の電荷分布は変わらず,中空導体球の外側の電場は変化しない.

今回はガウスの法則と導体内部の電場が$0$であることを使います.
ガウスの法則はこちらでも詳しく説明しています.
閉曲面を垂直に貫く電場を$E_{\perp}$(閉曲面を出ていくとき「+」,入るとき,「-」と約束します.),電場が貫く面積を$\varDelta S$,閉曲面内にある電荷の総和を$\sum{Q}$,クーロンの比例定数を$k_{0}$,誘電率を$\varepsilon_{0}$とすると
$E_{\perp}\cdot \varDelta S$の和$=4\pi k_{0}\sum{Q}=\dfrac{\sum{Q}}{\varepsilon_{0}}$
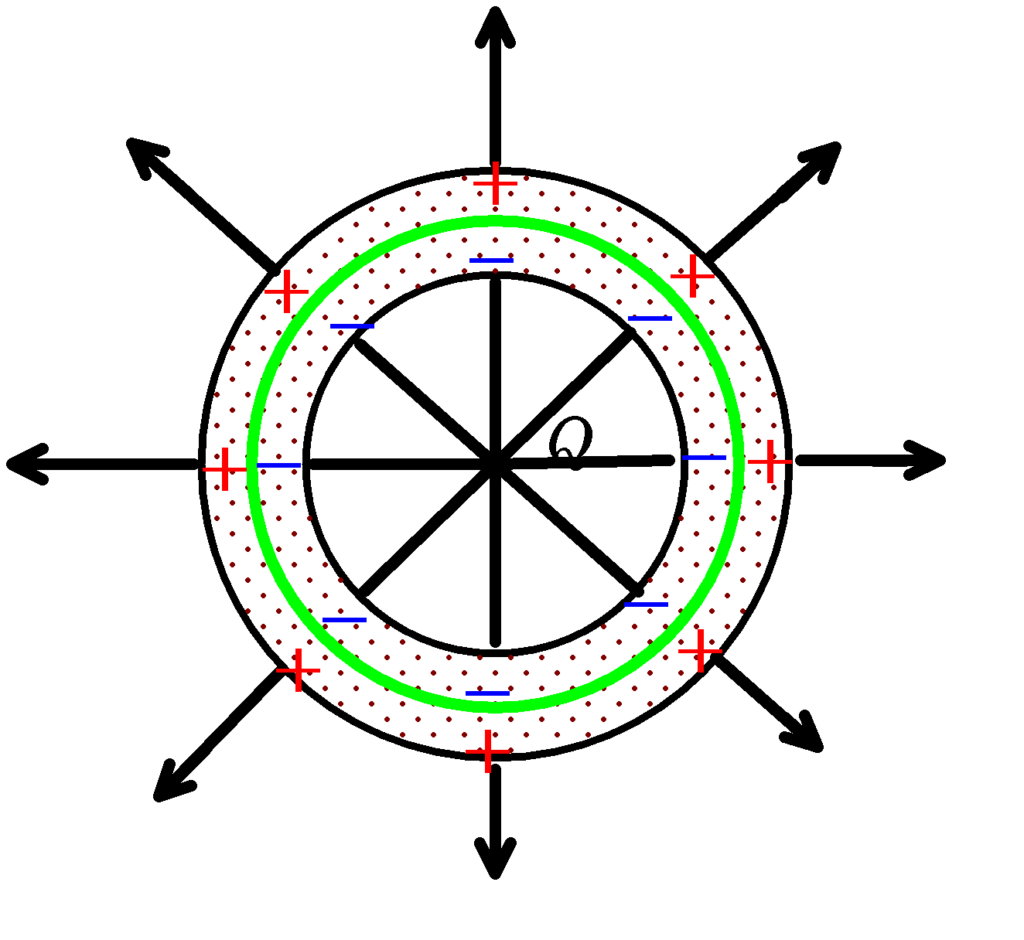

上図のように,中空導体球の中心に電荷$Q$を固定しましょう.あらかじめ,中空導体球には電荷が蓄えられていないとします.図のように中空導体の内側と外側の間に閉曲面をとります.(緑色の線)中空球導体の内側部分に分布している電荷の和を$Q_{1}$とすると,導体内部の電場が$0$なので,ガウスの法則より
★ ガウスの法則
$S$を電場が貫く面積とします.(ここでは具体的なことは考えないので計算はしません.)
$E\times S=4\pi k_{0}(Q+Q_{1})$
導体内部の電場は$0$,つまり上式において$E=0$より
$0=4\pi k_{0}(Q+Q_{1})$ $\therefore\,\, Q_{1}=-Q$

なるほど!中空導体球内側の電荷は導体内部の電場が$0$になるように分布するんだね.

はい.そして,中空導体球の外側に分布する電荷は電荷保存則を考えれば,$+Q$となりますが,外側の電荷はあってもなくても導体内部の電場は$0$となります.

ガウスの法則の式を立てたとき,中心にある電荷と中空導体球の内側の電荷しかでてきてからね.

そうですね.導体内部の電場は中心にある電荷と中空導体球内側に分布した電荷で$0$になるようになっています($\ast$).あとは,これをじゃましないように中空導体球の外側の電荷は一様に分布します.
そして,$(\ast)$からわかるように,仮に中心にある電荷を少し移動させても内側に分布する電荷の分布が変化するだけで外側の電荷は一様に分布したままです.
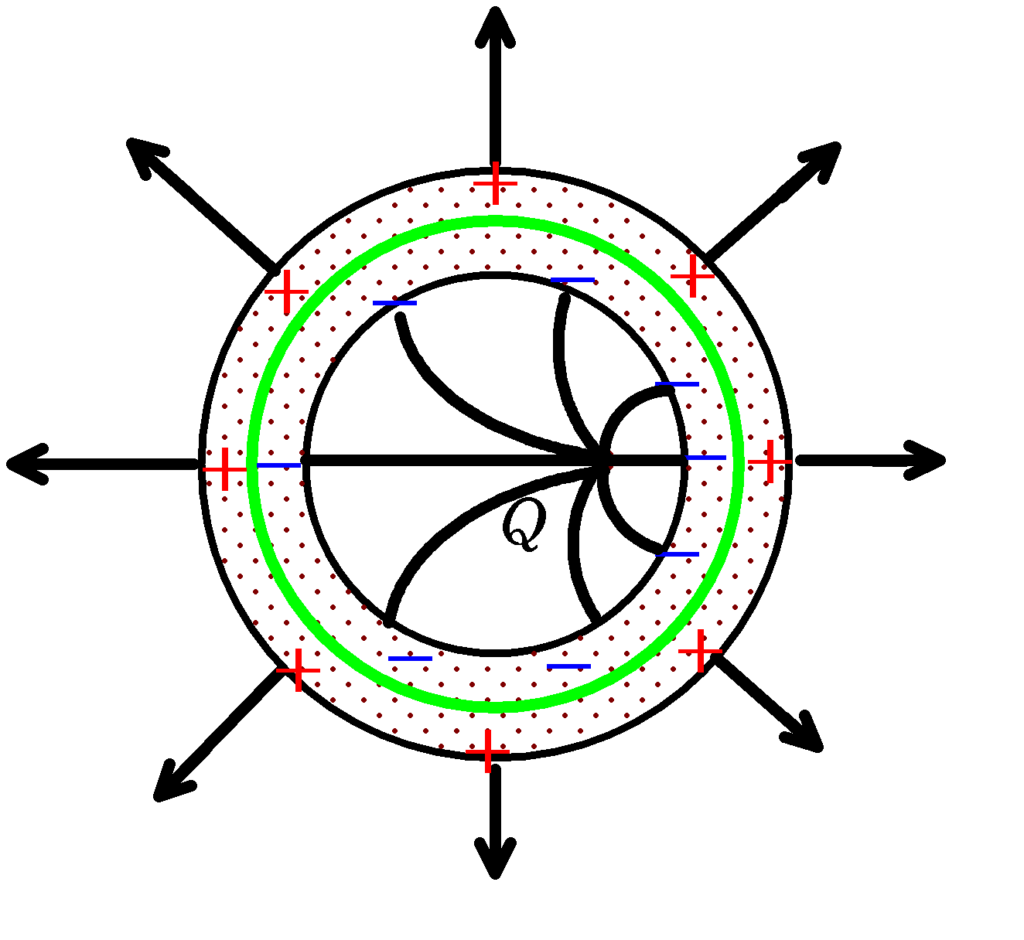

ちょっと不思議な感じもするけど,中心にあった電荷と内側で分布している電荷で導体内部の電場を$0$にしているんだから当たり前か.逆に外側の電荷分布が一様じゃなくなったら導体内部の電場が$0$にならないもんね.

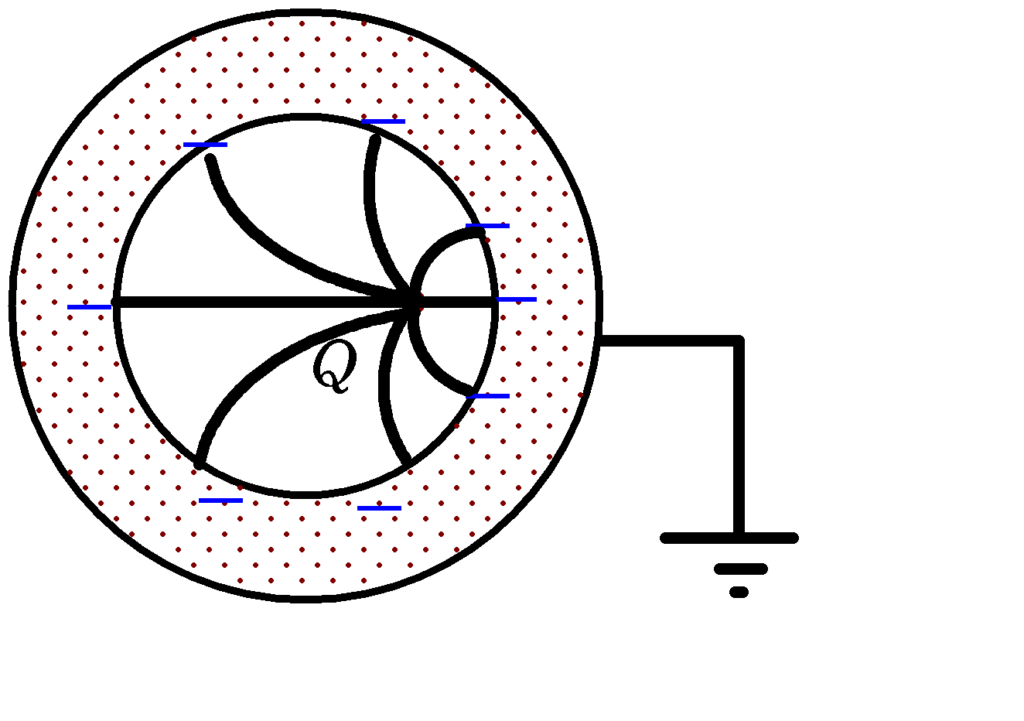
ちなみに,導体球を接地すると,導体と接地した部分の電位差がなくなるため,導体の外側の電場は$0$となります.つまり,外側の電荷は接地した部分に移動してしまいます.
まとめ

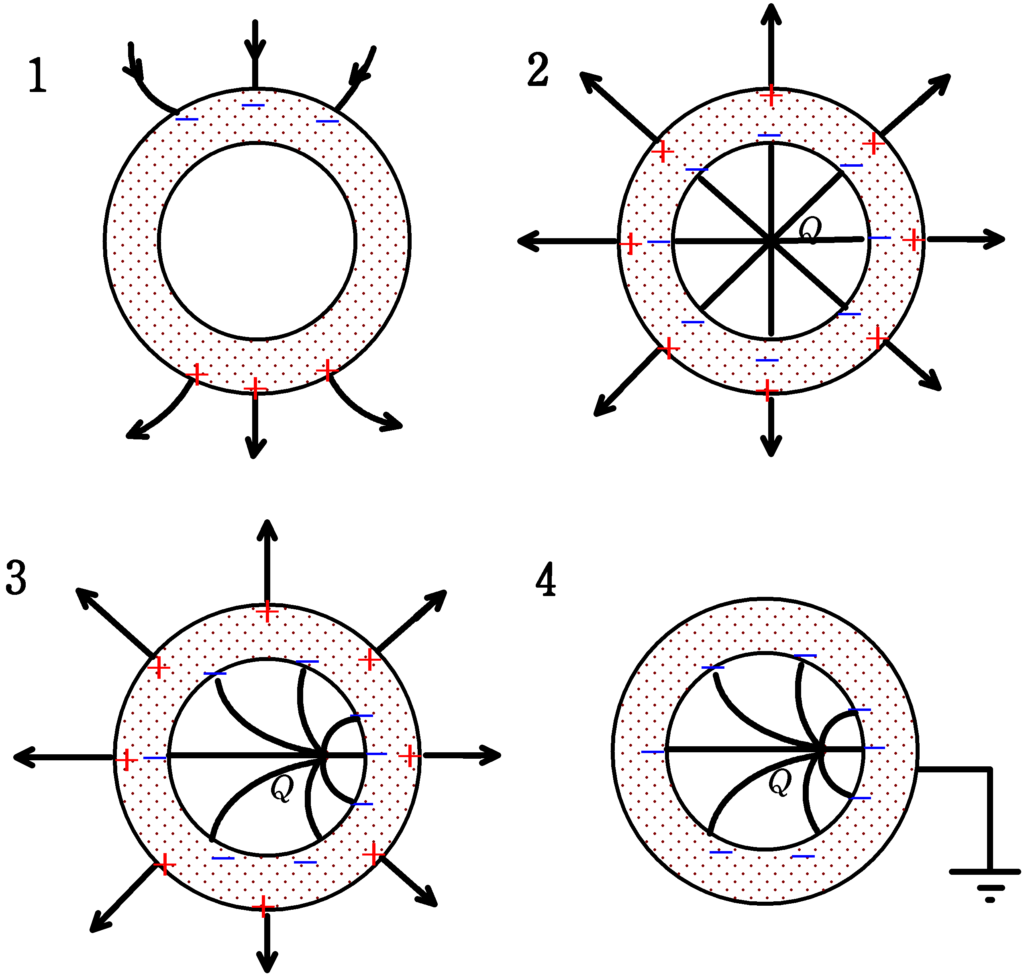
最後にまとめると次のようになります.
2,3において,中空導体球には電荷が蓄えられていないとする.
- 中空導体球内部に電荷がない場合,外部より電場がかけられても中空導体の中空部分には電場が生じず,導体球内側には電荷が分布しない.
- 中空導体球の中心に$+Q$の電荷が置かれているとき,内側には$-Q$の電荷が外側には$+Q$の電荷が一様に分布する.
- 2の状態から中心にあった電荷を移動させると内側部分の電荷の分布は変化するが,外側部分の電荷は一様分布のままである.その結果,導体球外側の電場は$2$の状態と同じである.
- 導体球を接地すると外側に分布していた電荷が設置している側に移動し,その結果導体球外側の電場は$0$となる.



コメント