
今回は次のような問題にどのように対応していけばよいのかを微分方程式を立てないで解こうと思います.
下の記事では,微分方程式を立てて解きました.
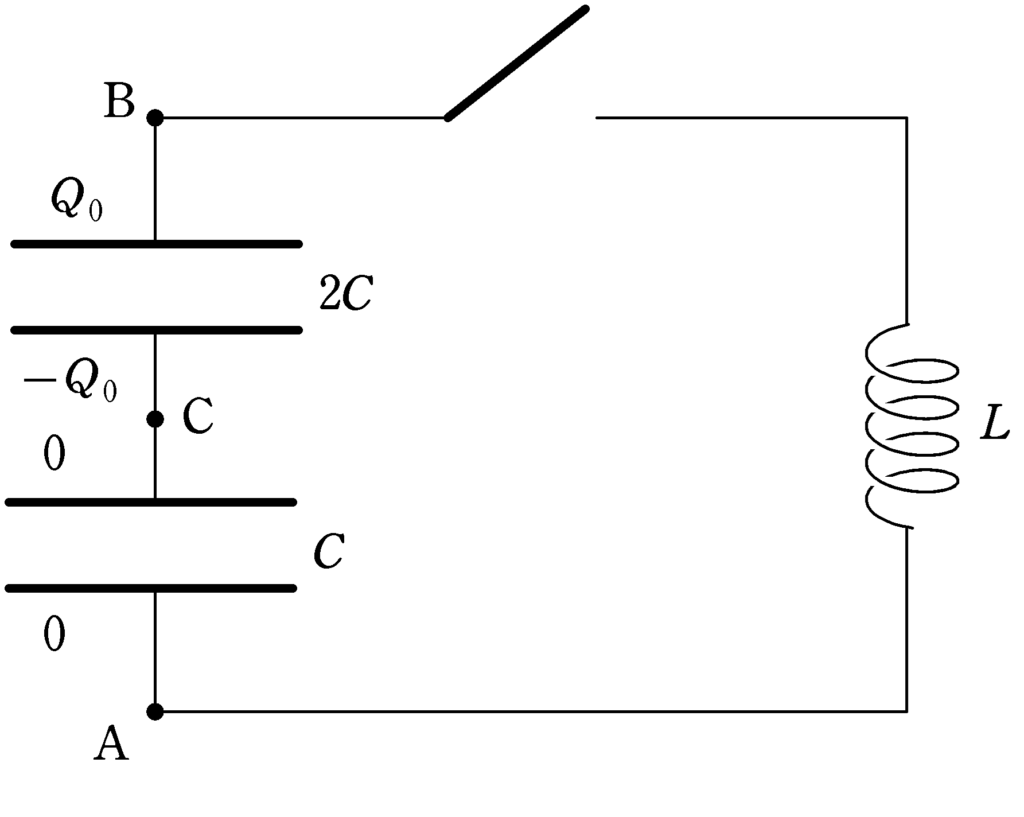
上図のように,電気容量$2C , C$のコンデンサーと,自己インダクタンス$L$の抵抗のないコイル,スイッチがある.はじめ,スイッチは開かれていて,電気容量$2C$のコンデンサーには,電気量$Q_{0}$の電荷が蓄えられており,電気容量$C$のコンデンサーには,電荷が蓄えらえれていない.ある時刻にスイッチを閉じたところ,電気振動が行った.このとき,コイルに流れる電流の大きさの最大値を$Q_{0} , C , L$を用いて表せ.

このとき,次のことはあらかじめ知っておきましょう.
- 電流の大きさが最大になるときは電流を$i$として,$\dfrac{\varDelta i}{\varDelta t}=0$のときである.したがって,コイルの誘導起電力は0である.
- 静電エネルギー+コイルに蓄えられるエネルギー=一定 が成り立つ.

なんで,電流の大きさがが最大になるときに誘導起電力が0になるの??
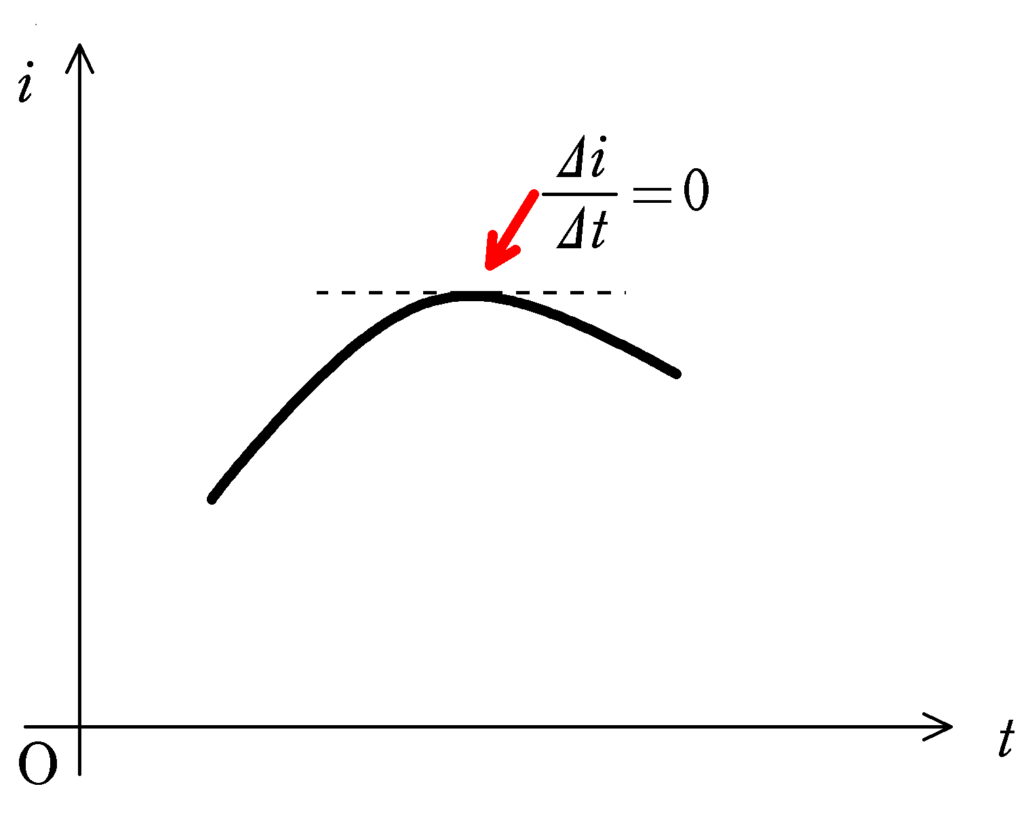

上図のように,電流が最大値になる場合は傾きが$0$になります.
したがって,$\dfrac{\varDelta i}{\varDelta t}=0$となります.
そして,コイルの誘導起電力の大きさ$V$は自己インダクタンスを$L$として,
$V=L\left|\dfrac{\varDelta i}{\varDelta t}\right|$
なので, $\dfrac{\varDelta i}{\varDelta t}=0$ より,$V=0$となるわけです.
では,電流が最大になるとき,すなわち,コイルに生じる誘導起電力が0のときのそれぞれのコンデンサーに蓄えられている電荷を求めていきましょう.
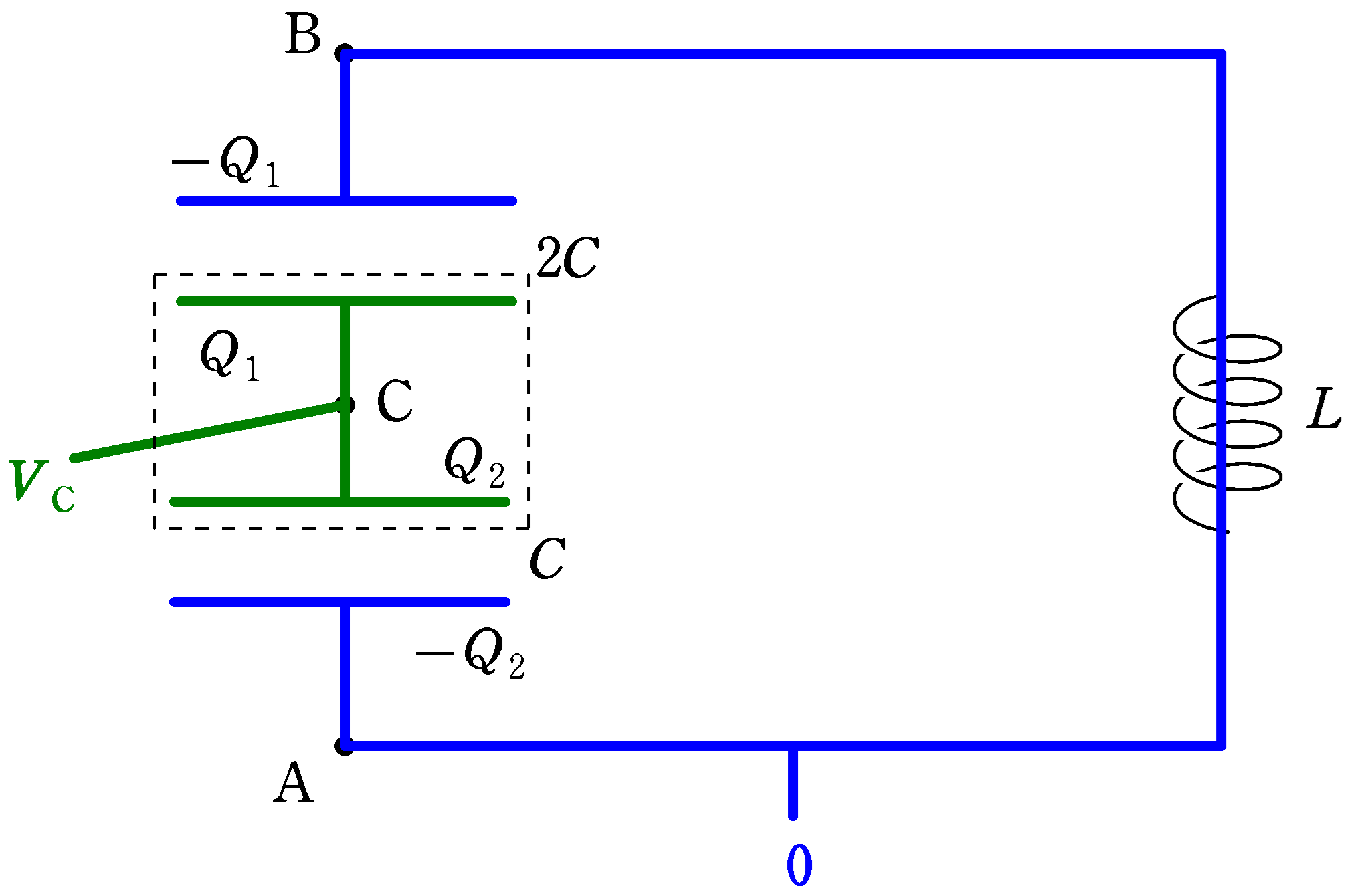
電荷は下図のように設定します.
また,下図の青色部分の電位を0,緑色部分の電位を$V_{\rm C}$として,電荷保存則とコンデンサーの式を立てていきましょう.
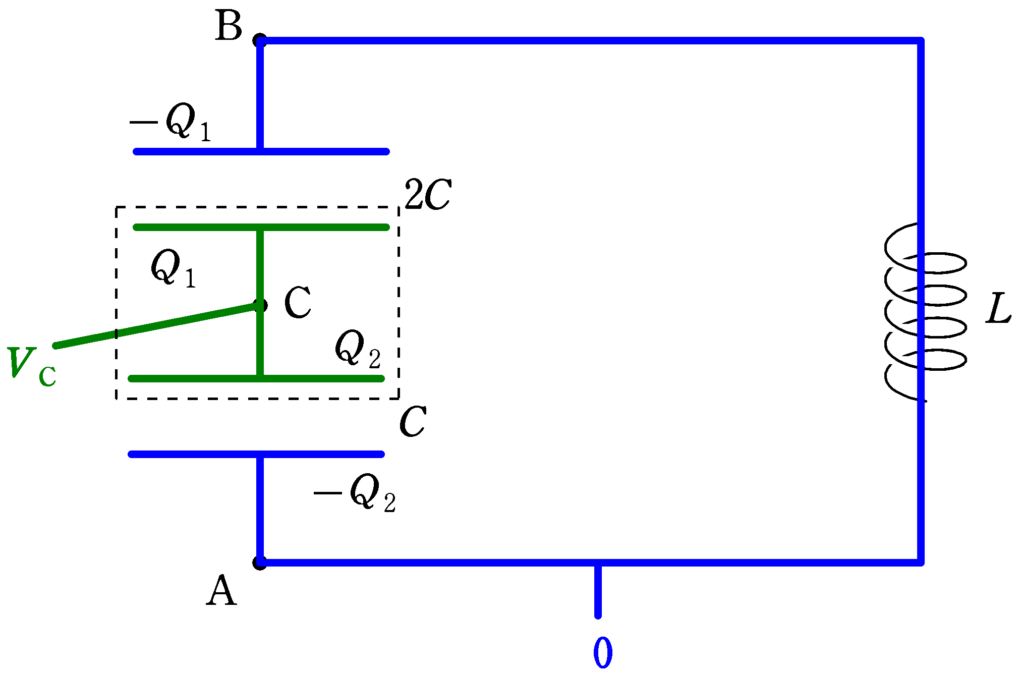
★ 電荷保存則
$Q_{1}+Q_{2}=-Q_{0}$ $\dots (\ast)$
★ コンデンサーの式
$Q_{1}=2CV_{\rm C}$ $\dots (2\ast)$
$Q_{2}=CV_{\rm C}$ $\dots (3\ast)$
$(2\ast)$,$(3\ast)$を$(\ast)$を代入すると
$2CV_{\rm C}+CV_{\rm C}=-Q_{0}$
$\therefore V_{\rm C}=-\dfrac{Q_{0}}{3C}$
したがって,$(\ast)$,$(2\ast)$より
$Q_{1}=-\dfrac{2}{3}Q_{0}$,$Q_{2}=-\dfrac{1}{3}Q_{0}$

この結果から,電流の最大値$I_{\rm max}$を,エネルギー保存則で求めましょう.
ちなみに,容量$C$に電荷$q$が蓄えられているときの静電エネルギー$U_{1}$は
$U_{1}=\dfrac{q^{2}}{2C}$
であり,自己インダクタンス$L$のコイルに電流$i$が流れているときのコイルに蓄えられているエネルギーは
$U_{2}=\dfrac{1}{2}Li^{2}$
です.
今回は
$\dfrac{q^{2}}{2C}+\dfrac{1}{2}Li^{2}=$一定
の式を立てます.
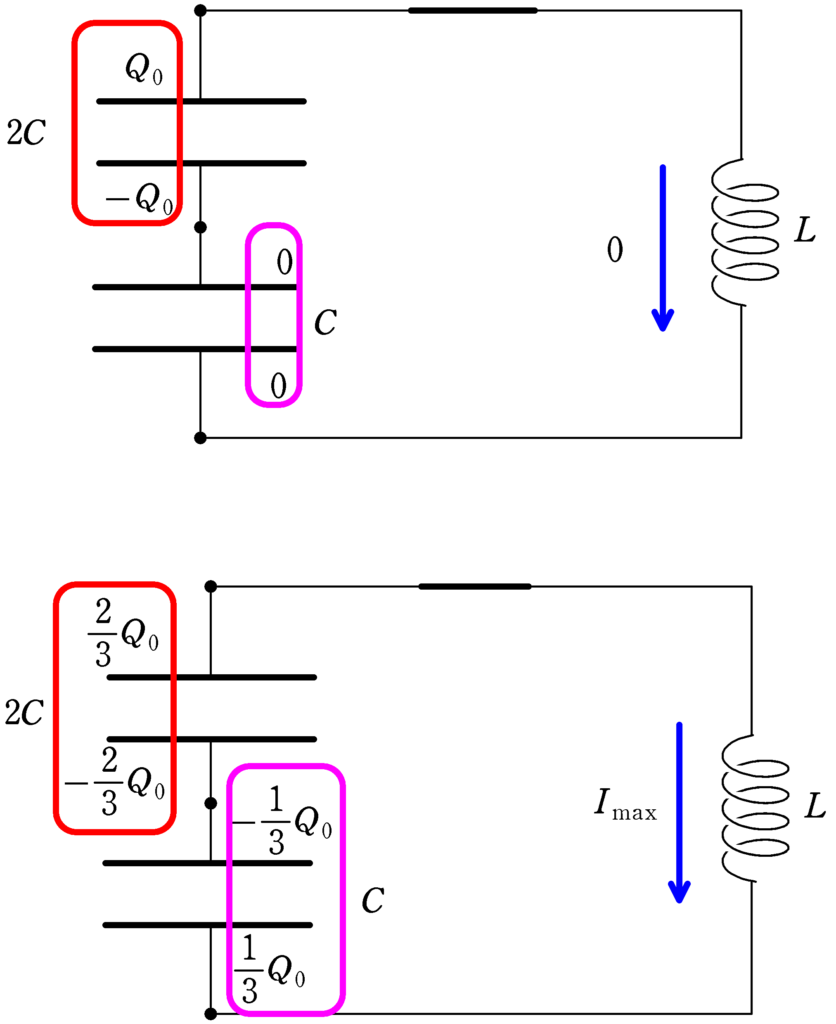
★ エネルギー保存則
$\dfrac{Q_{0}^{2}}{2\cdot 2C}+\dfrac{0^{2}}{2C}+\dfrac{1}{2}L\cdot 0^{2}=\dfrac{\left(-\dfrac{2Q_{0}}{3}\right)^{2}}{2\cdot 2C}+\dfrac{\left(-\dfrac{Q_{0}}{3}\right)^{2}}{2C}+\dfrac{1}{2}LI_{\rm max}^{2}$
$I_{\rm max}$について解く
$\eqalign{\dfrac{1}{2}LI_{\rm max}^{2}&=\dfrac{Q_{0}^{2}}{2C}\left(\dfrac{1}{2}-\dfrac{1}{2}\cdot \dfrac{4}{9}-\dfrac{1}{9}\right)\\&=\dfrac{Q_{0}^{2}}{12C}}$
$\therefore I_{\rm max}=\dfrac{Q_{0}}{\sqrt{6LC}}$ (答)

前回の内容と同じになったね.



コメント