
今回はクーロン力(静電気力)による単振動を扱います.その前に,高校物理でよく出る近似式を確認しましょう!
$|\alpha|\ll1$のとき
$(1+\alpha)^n\fallingdotseq 1+n\alpha$

問題文では
$a\ll b$ や $b$ は $a$ に比べて十分大きい
のような表現をします.これを
$\dfrac{a}{b}\ll1$
として,小さい数を作りましょう.このとき,$\alpha =\dfrac{a}{b}$と対応します.
さて,問題です!
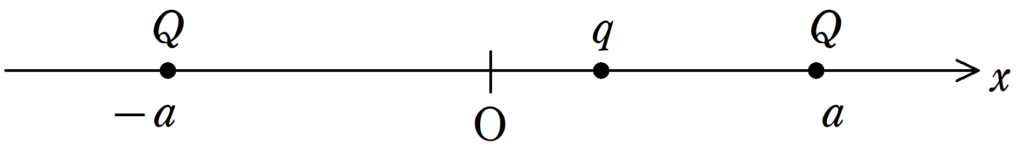
$xy$直交座標のA$(-a,0)$とB$(a,0)$にそれぞれ電気量$Q$$(Q>0)$の電荷が固定されている.さらに,質量$m$で電気量$q$$(q>0)$の電荷Xを$(c,0)$$(c>0)$の位置に静かにおいたところ電荷Xは単振動をした.ただし,$a$は$c$に比べて十分大きいものとし,クーロンの比例定数を$k_{0}$とする.また,電荷Xの運動によって生じる磁場は無視をするものとする.
(1) 電荷Xが座標$x$にいるときの加速度を$x$軸の正の向きに$\alpha$とする.このとき,電荷Xの運動方程式を$m$,$\alpha$,$k_{0}$,$Q$,$q$,$x$,$a$を用いて立てよ.
(2) $|\alpha|\ll 1$のとき,$(1+\alpha)^n\fallingdotseq 1+n\alpha$の近似ができるとする.(1)の運動方程式をこの近似式を用いて近似し,単振動をすることを確かめよ.ただし,$x\ll a$である.
(3) (2)より,電荷Xの振動の中心$x_{0}$,角振動数$\omega$,振動の周期$T$を求めよ.
(4) 電荷Xが運動をはじめた時刻を$t=0$とする.時刻$t$における位置$x$を$c$,$m$,$k_{0}$,$Q$,$q$,$a$,$t$から必要なものを用いて表せ.
(5) 電荷Xが原点を通るときの速さを単振動のエネルギー保存を用いて計算せよ.答えは$c$,$m$,$k_{0}$,$Q$,$q$,$a$から必要なものを用いて表せ.

$Q$と$q$の電荷が距離$r$離れているときにはたらくクーロン力(静電気力)の大きさ$|F|$は次のように表されるんだったね.(クーロンの比例定数を$k_{0}$とする)
$|F|=k_{0}\dfrac{|Q||q|}{r^2}$
もし,$Q$と$q$が同符号の電荷(つまり,$+$と$+$または$-$と$-$)だったら,斥力(反発する力)がはたらいて,異符号の電荷だったら,引力がはたらくんだったね.
<解答>
(1)
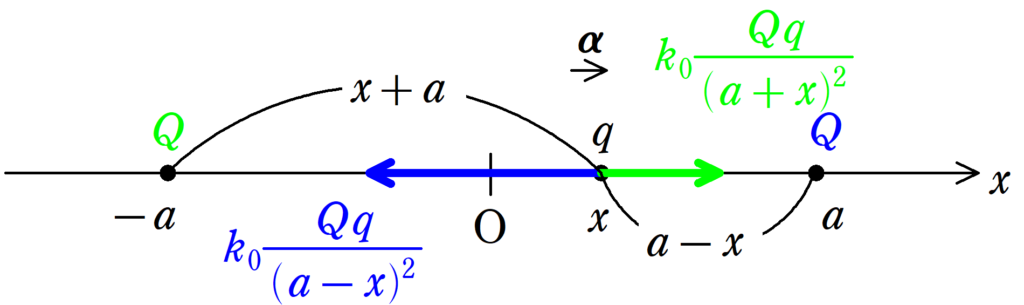
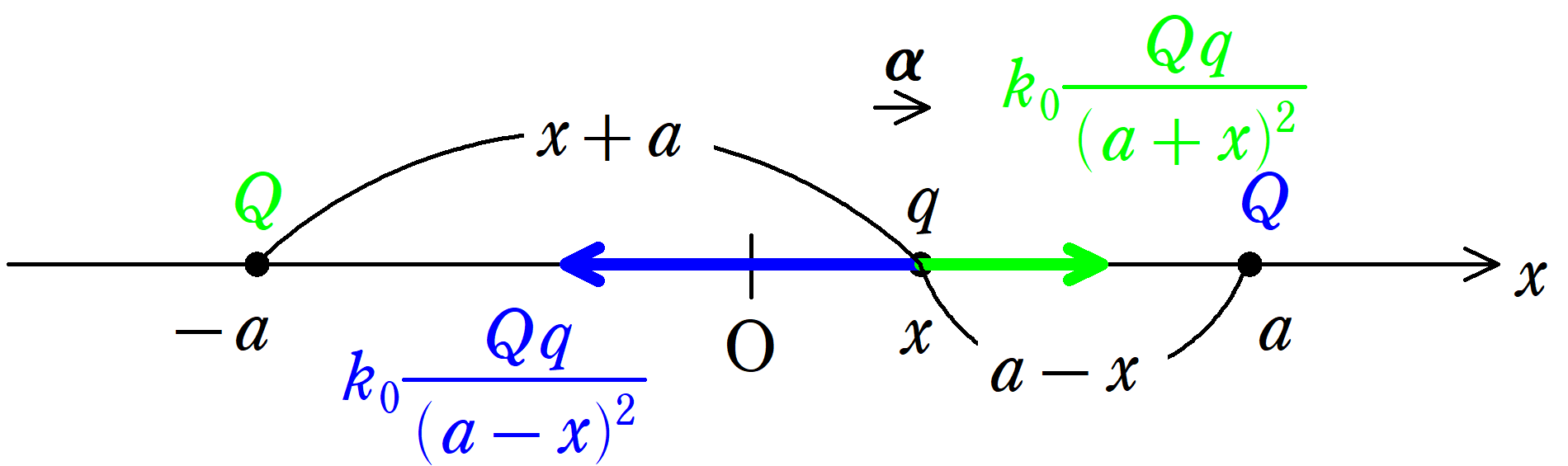
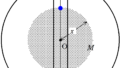
位置$x$にあるとき(今回も$x>0$のときの図です)の電荷$q$にはたらく力を図示すると上のようになります.緑の方の電荷と$q$はどちらも正の電荷なので反発する$x$軸の正の向きに,青の電荷と$q$もどちらも正の電荷なので反発する$x$軸の負の向きに力がはたらいています.したがって,運動方程式は
$m\alpha =k_{0}\dfrac{Qq}{(a+x)^2}-k_{0}\dfrac{Qq}{(a-x)^2}$ $\dots (\ast)$
(2) $x\ll a$なので,$\dfrac{x}{a}\ll 1$です.$(1+\alpha)^n\fallingdotseq 1+n\alpha$の近似式を使うには$\dfrac{x}{a}$をつくる必要があります.
$\dfrac{1}{(a+x)^2}=\dfrac{1}{a^2}\cdot \dfrac{1}{(1+\dfrac{x}{a})^2}=\dfrac{1}{a^2}\cdot(1+\dfrac{x}{a})^{-2}\fallingdotseq \dfrac{1}{a^2}\cdot (1-2\dfrac{x}{a})$
$\dfrac{1}{(a-x)^2}=\dfrac{1}{a^2}\cdot \dfrac{1}{(1-\dfrac{x}{a})^2}=\dfrac{1}{a^2}\cdot(1-\dfrac{x}{a})^{-2}\fallingdotseq \dfrac{1}{a^2}\cdot (1+2\dfrac{x}{a})$
これらの近似式を使って$(\ast)$は
$\eqalign{m\alpha &=k_{0}Qq\{\dfrac{1}{(a+x)^2}-\dfrac{1}{(a-x)^2}\}\\&\fallingdotseq k_{0}Qq\{\dfrac{1}{a^2}\cdot (1-2\dfrac{x}{a})-\dfrac{1}{a^2}\cdot (1+2\dfrac{x}{a})\}\\&=-\dfrac{4k_{0}Qq}{a^3}x}$
これは単振動の運動方程式になっていますね!
(3) (2)で得た運動方程式より,振動の中心は$x_{0}=0$,角振動数は
$\omega=\sqrt{\dfrac{\dfrac{4k_{0}Qq}{a^3}}{m}}=\dfrac{2}{a}\sqrt{\dfrac{k_{0}Qq}{ma}}$
となります.また,周期$T$は$T=\dfrac{2\pi}{\omega}$の関係より
$T=\dfrac{2\pi}{\omega}=\pi a\sqrt{\dfrac{ma}{k_{0}Qq}}$
(4) 振動の中心が$x_{0}=0$で最高点$c$から速度0でスタートして$x$軸の負の向きにいくので,$\cos$型ですね.振幅は$c$です.
$x=x_{0}+A\cos \omega t=c \cos \dfrac{2}{a}\sqrt{\dfrac{k_{0}Qq}{ma}}t$
(5) さて,原点における速さを前回扱った単振動のエネルギー保存を使って計算しましょう.
$m\alpha =-\dfrac{4k_{0}Qq}{a^3}x$
から,
$\dfrac{1}{2}mv^2+\dfrac{1}{2}(\dfrac{4k_{0}Qq}{a^3})x^2=$一定
と変形します.これを$x=c$と$x=0$の場所とで結びます.$x=c$では$v=0$です.$x=0$での速さを$v=V$としましょう.
$\eqalign{\dfrac{1}{2}m\cdot 0^2+\dfrac{1}{2}(\dfrac{4k_{0}Qq}{a^3})c^2&=\dfrac{1}{2}mV^2+\dfrac{1}{2}(\dfrac{4k_{0}Qq}{a^3})\cdot 0^2\cr \dfrac{1}{2}mV^2&=\dfrac{1}{2}(\dfrac{4k_{0}Qq}{a^3})c^2\cr V^2&=\dfrac{4k_{0}Qqc^2}{ma^3}\cr V&=\dfrac{2c}{a}\sqrt{\dfrac{k_{0}Qq}{ma}}}$
以上より,$V=\dfrac{2c}{a}\sqrt{\dfrac{k_{0}Qq}{ma}}$

今回これでおしまいです.近似も出てきて難しくなってきたけど,単振動の運動方程式がでてきたら今までと一緒だね.
次回の内容はこちら



コメント
[…] […]
[…] […]