問題
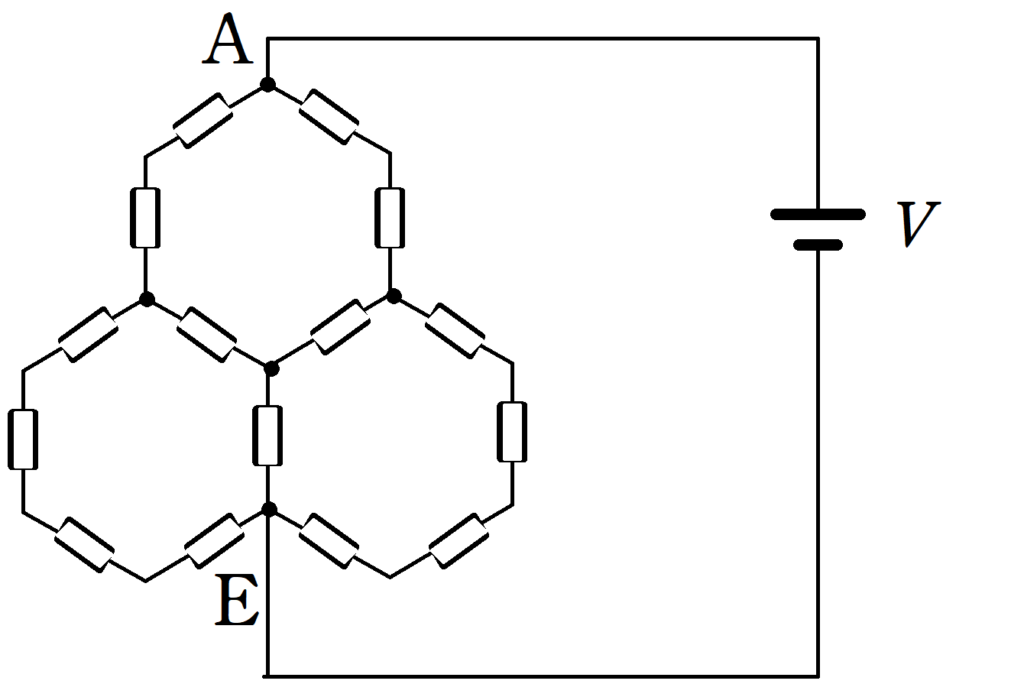
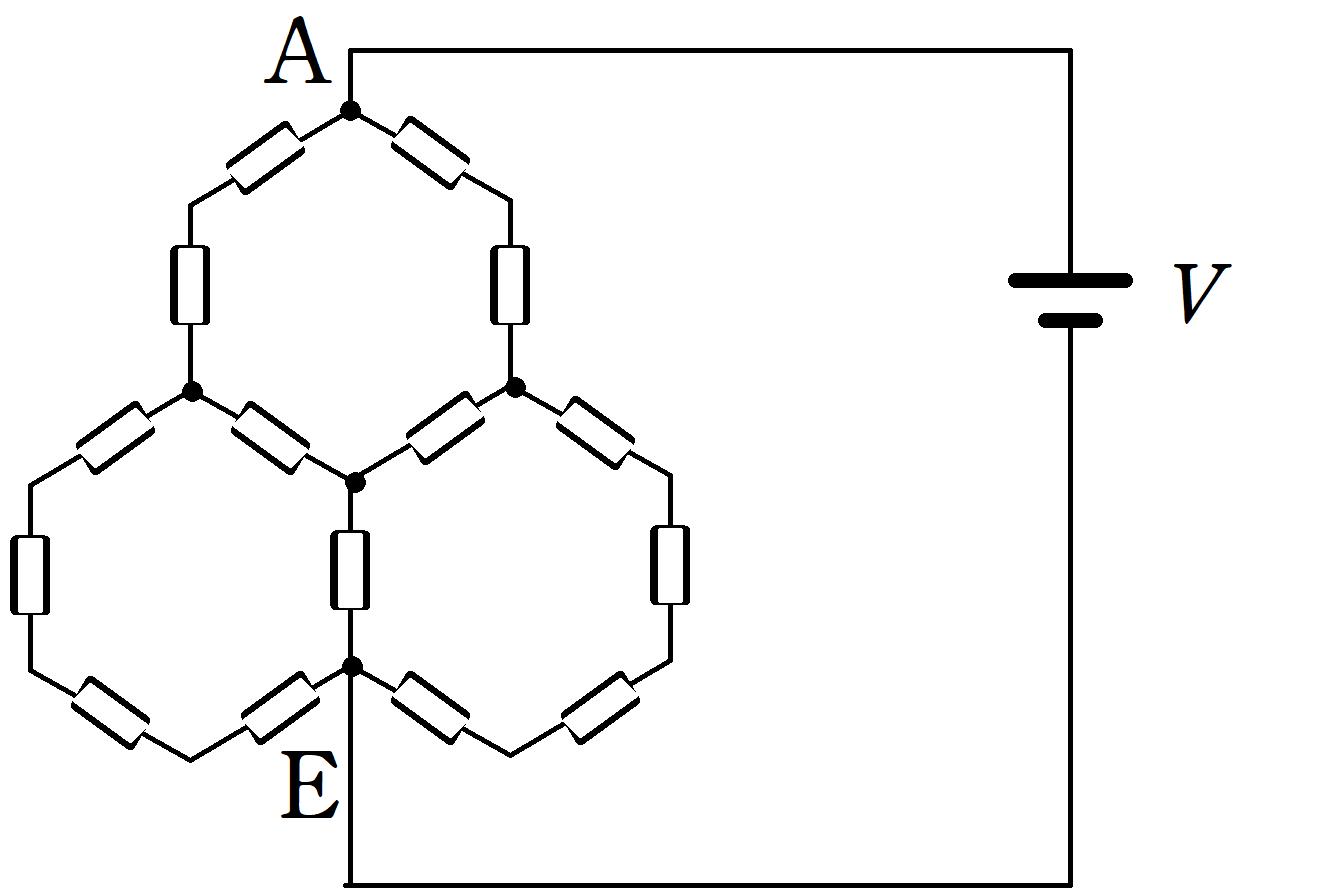
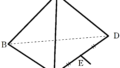
抵抗値$R$の15個の抵抗を使って上図のような回路を作った.
このとき,AE間の合成抵抗を$R$を用いて表せ.
<解答>
オームの法則
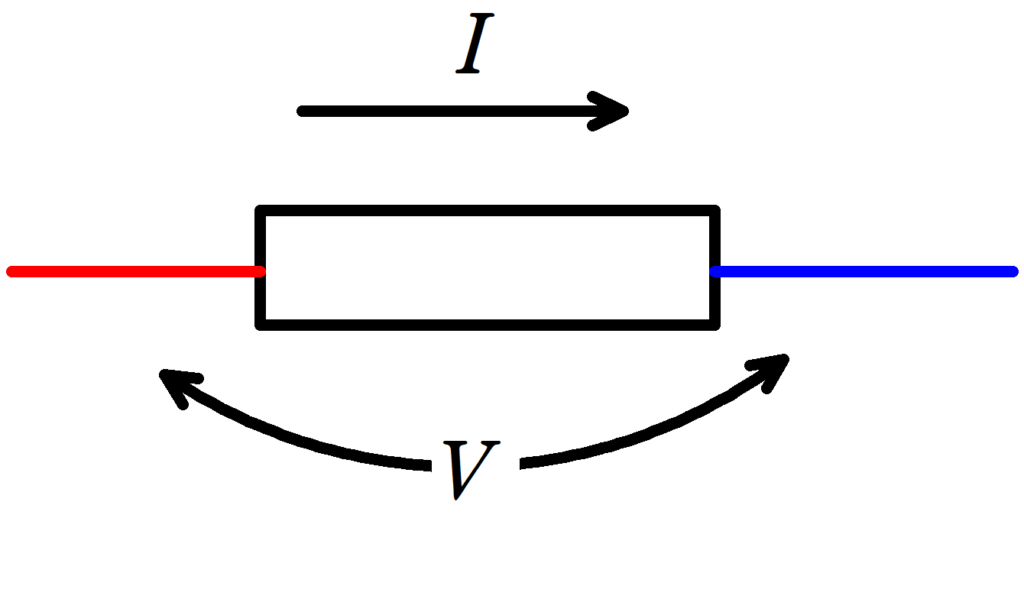
抵抗に流れる電流が$I$,電圧を$V$,抵抗値を$R$とするとき,
$V=RI$
が成り立つ.
合成抵抗を求めるときは,$\dfrac{V}{I}$を計算する.

NEKO
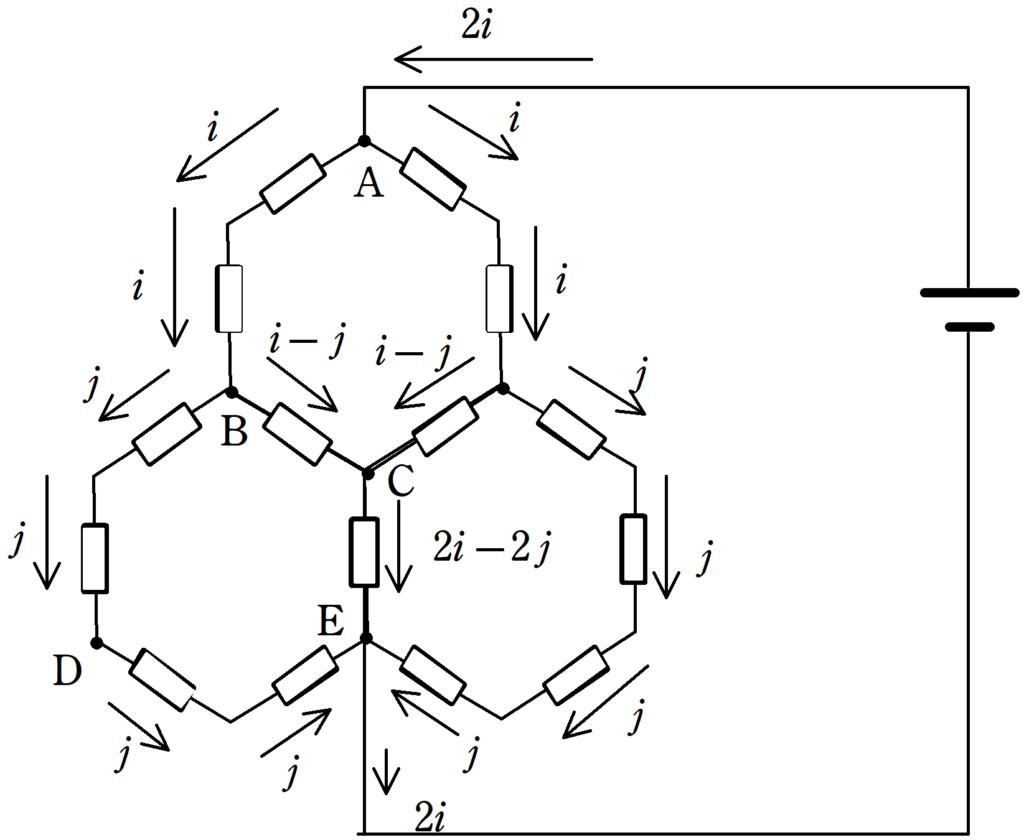
対称性を考慮して,電流を設定します.
Aから流入した電流は左右に大きさ$i$の電流に分かれたとします.
さらに,Bにて左に$j$,右に$i-j$の電流が流れます.
Cには,左からくる電流$i-j$と右からくる電流$i-j$が合流してCE間には$2i-2j$の電流が流れます.
Eには,左から$j$右から$j$,上から$2i-2j$の電流が流れて,$2i$の電流として出ていきます.
Eでの電位を$0$,Aでの電位を$V$として,次の経路のキルヒホッフ則を立てましょう.
★ A→B→D→E経路のキルヒホッフ則
$V-Ri\times 2-Rj\times 4=0$
$\therefore 2i+4j=\dfrac{V}{R}$ $\dots (\ast)$
★ A→B→C→E経路のキルヒホッフ則
$V-Ri\times 2-R(i-j)-R(2i-2j)=0$
$\therefore 5i-3j=\dfrac{V}{R}$ $\dots (2\ast)$
$(\ast)$,$(2\ast)$より,$i=\dfrac{7V}{26R}$,$j=\dfrac{3V}{26R}$
したがって,Aに流れ込みEから出ていく電流は$2i=\dfrac{7V}{13R}$
もとめる合成抵抗は,$\dfrac{V}{2i}=\dfrac{13}{7}R$(答)

コメント
最後の答えは13R/7ではないでしょうか。
ご指摘ありがとうございます。
訂正しました.
点Bにおいて、iが(1/2)iずつ左右に分かれないのはなぜですか?同じ抵抗値なら1/2されると思ったのですが…
感覚的に考えると,「その先にある抵抗に対称性がないから」ですかね.Bの左側は4個,右側は2個ですし.怪しかったら別な文字に設定するのが無難かと思います.