
今回は,平面波の波の式です.
平面上の1点の入射波の媒質の振動がわかっているとき,平面全体の振動の様子を計算する問題です.

今回の問題を解くにあたって,ベクトルの内積を利用するので,整理しておきましょう.
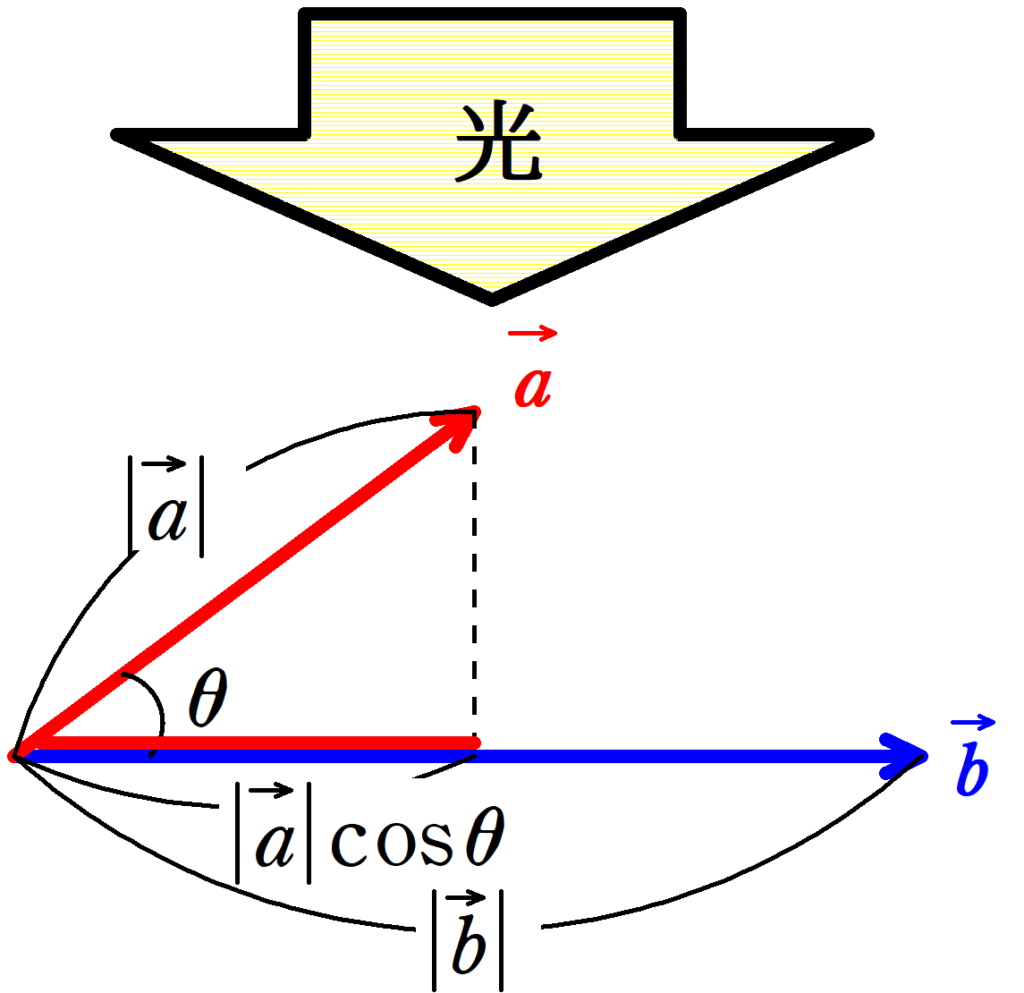
$\vec{a}$と$\vec{b}$のなす角を$\theta$とすると,内積を次のように定義する.
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$

内積は,$\vec{b}$に垂直な光を当てたときの$\vec{a}$の影の長さと$\vec{b}$の長さの積になっているんだね.(向きが逆方向同士の積は負になっているよ)

内積を確認したところで,次の補題を解いてみましょう.
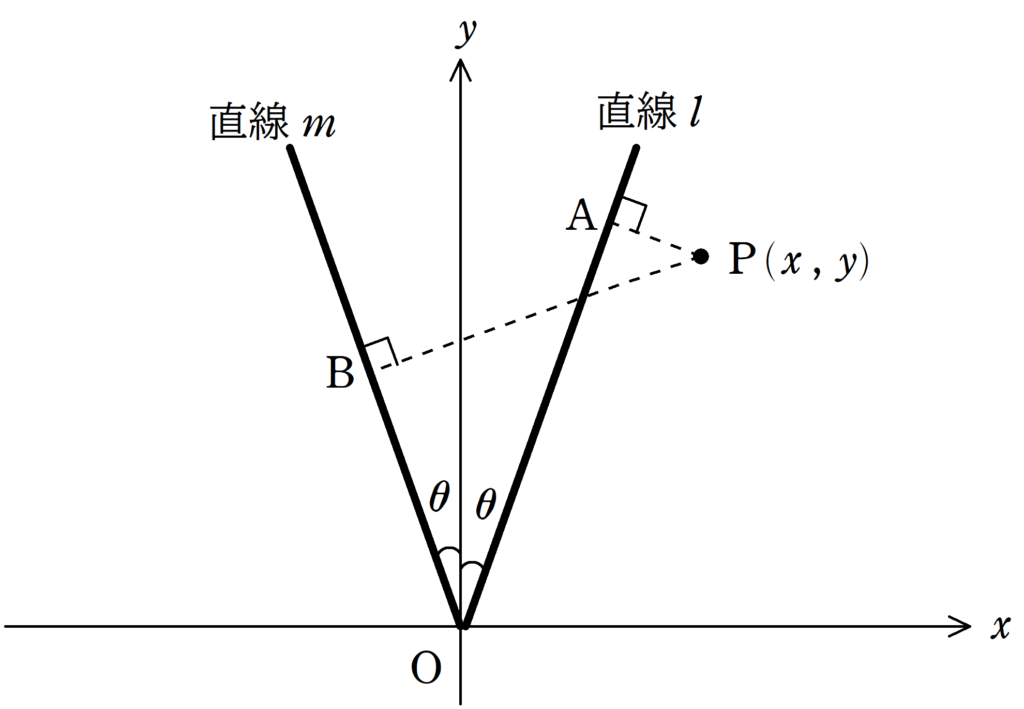
原点を$\rm O$とする$x-y$座標をとる.
$y$軸より,時計回りに$\theta$$(0<\theta <\dfrac{\pi}{2})$回転した方向に直線$l$があり,反時計回りに$\theta$回転した方向に直線$m$がある.
$x-y$平面上の点${\rm P}(x,y)$より,直線$l , m$に垂線を引いたとき,垂線の足をそれぞれ$\rm A , B$とする.
このとき,距離$\rm OA$と距離$\rm OB$の距離を$x , y , \theta$を用いて表せ.
<解答>

この問題は,直線$l$や直線$m$の方向の単位ベクトルを利用することで,簡単に計算することができます.

単位ベクトルは大きさ$1$のベクトルのことだよね.
直線$l$の方向の単位ベクトルを$\vec{e_{1}}$,直線$m$の方向の単位ベクトルを$\vec{e_{2}}$とすると,それぞれ
$\vec{e_{1}}=(\sin\theta , \cos\theta)$
$\vec{e_{2}}=(-\sin\theta , \cos\theta)$
となるね.
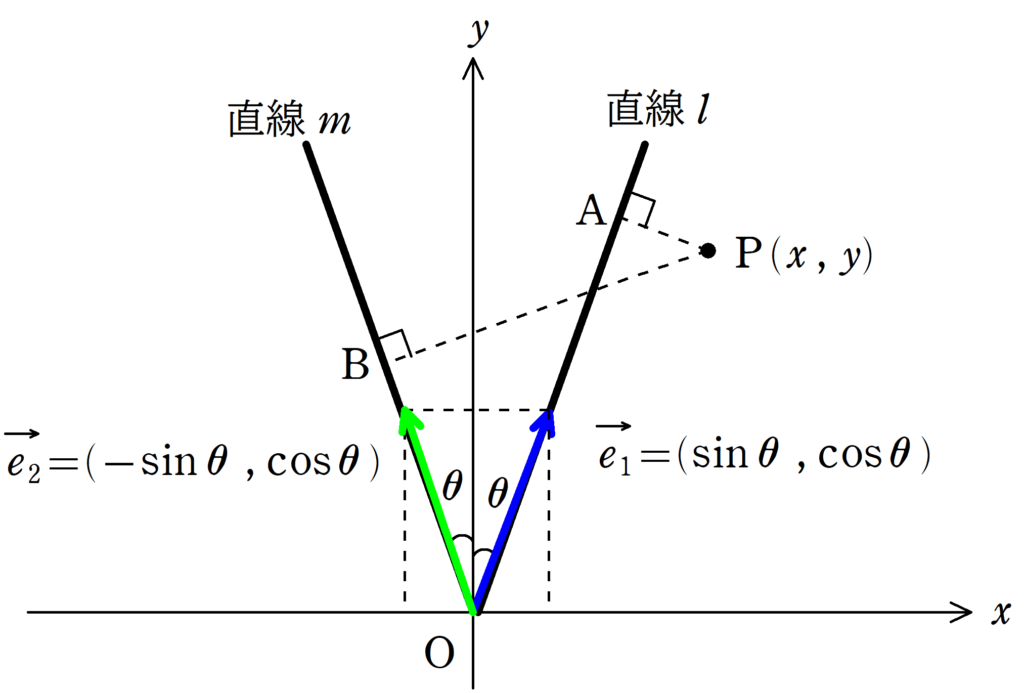

$\rm \vec{OP}$と$\vec{e_{1}}$の内積を考えましょう.
これは,$\vec{e_{1}}$に垂直な光を当てたときの$\rm \vec{OP}$の影の長さと$\vec{e_{1}}$の長さの積となります.
ただ,$\vec{e_{1}}$の長さは1なので,$\rm \vec{OP}$と$\vec{e_{1}}$の内積は結局$\rm \vec{OP}$の長さになるわけです.
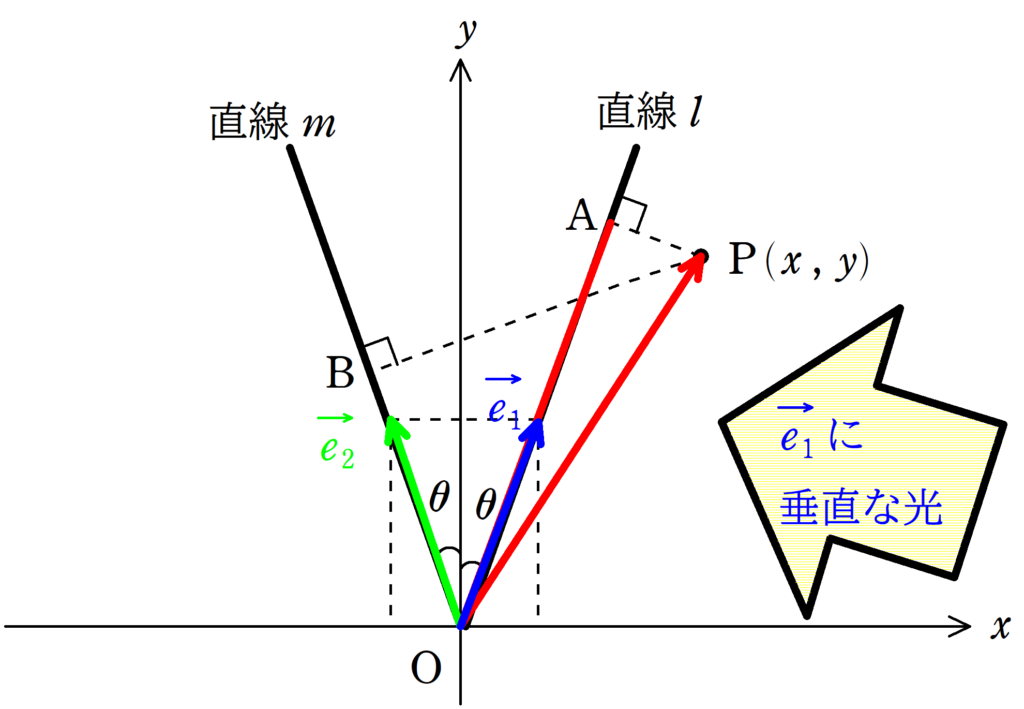

内積の計算は次のようにするんだよね.
$\vec{a}=(a_{1} , a_{2})$,$\vec{b}=(b_{1} , b_{2})$の内積$\vec{a}\cdot \vec{b}$は次のようになる.
$\eqalign{\vec{a}\cdot \vec{b}&=(a_{1}, a_{2})\cdot (b_{1} , b_{2})\\&=a_{1}b_{1}+a_{2}b_{2}}$
$\eqalign{{\rm OA}&=\vec{\rm OP}\cdot \vec{e_{1}}\\&=(x , y)\cdot (\sin\theta , \cos\theta)\\&=x\sin\theta +y\cos\theta}$

同様に,$\rm OB$も計算しましょう!
$\rm OB$は$\vec{\rm OP}\cdot \vec{e_{2}}$を計算すればいいね.
$\eqalign{{\rm OB}&={\rm OP}\cdot \vec{e_{2}}\\&=(x , y)\cdot (-\sin\theta , \cos\theta)\\&=-x\sin\theta+y\cos\theta}$
答:${\rm OA}=x\sin\theta +y\cos\theta$,${\rm OB}=-x\sin\theta +y\cos\theta$

でも,なんでこれを求めたの??

これを平面波の式の導出で使うからです.
それでは,問題を解いてみましょう.
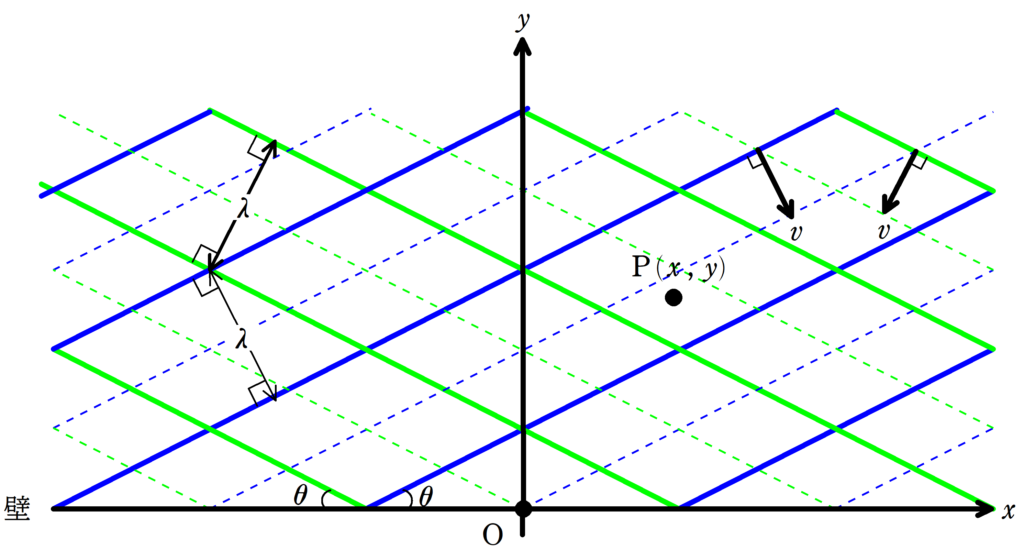
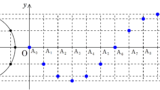
上図のように,波長$\lambda$の波面が$x$軸の正方向からのなす角$\theta$の方向より自由端である$x$軸入射し,$\pi -\theta$の方向に反射している.
入射波,反射波の速さはともに$v$である.
時刻$t$において,原点Oの入射波の媒質の変位$y_{\rm O}$を観測したところ,振幅$A$,周期$T$を用いて次のように表された.
$y_{\rm O}=A\sin \dfrac{2\pi}{T}t$
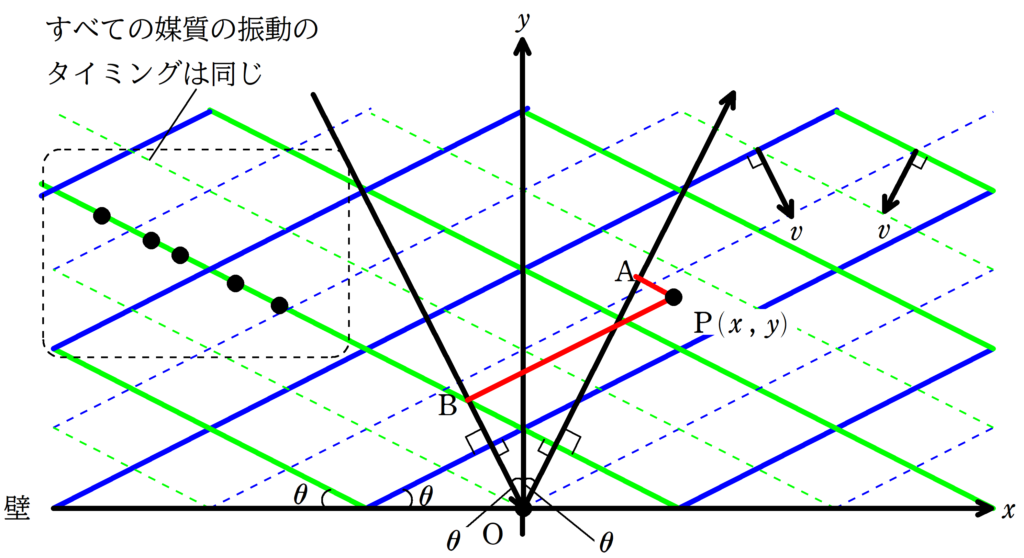
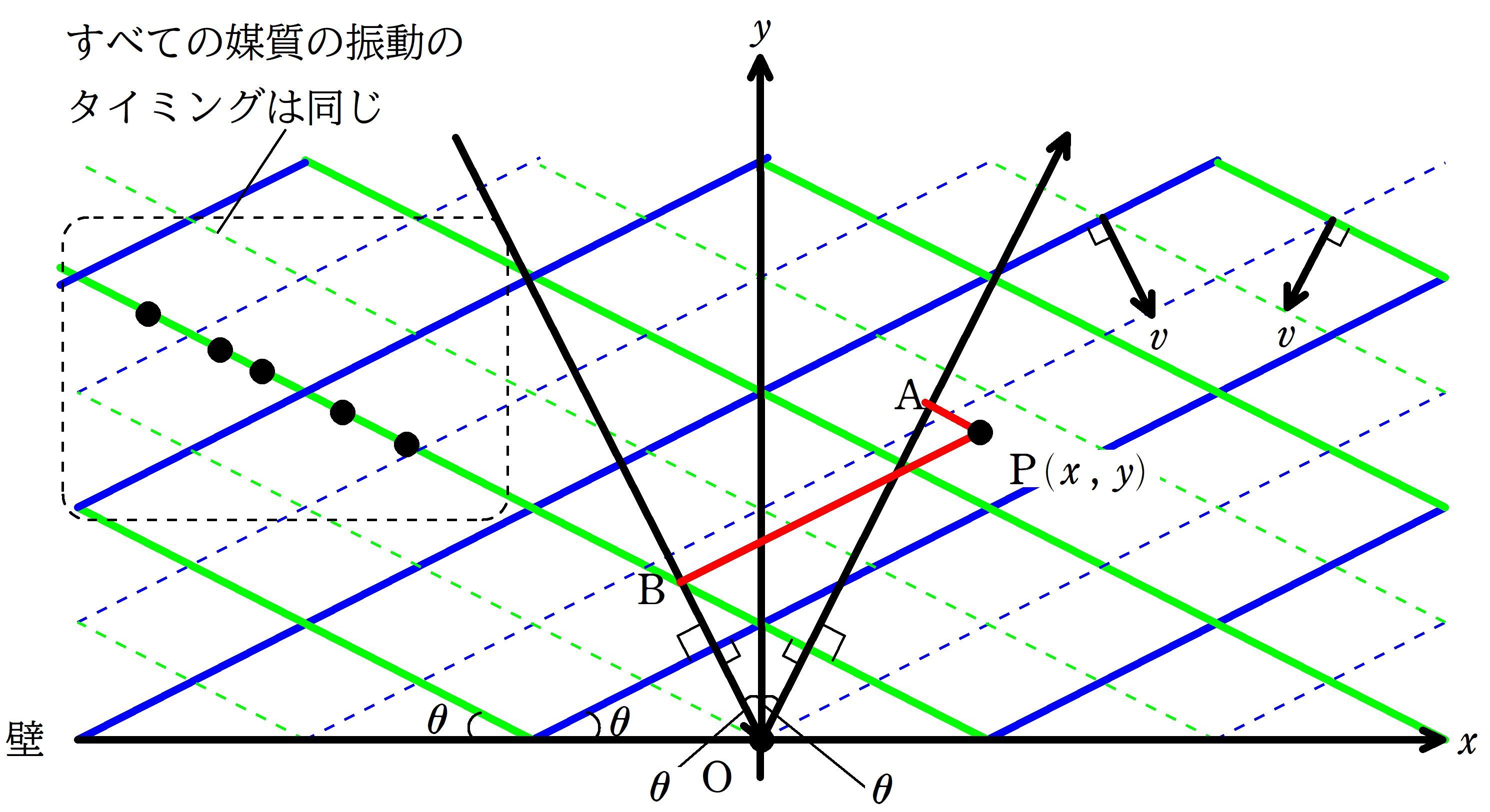
${\rm P}(x , y)$より,入射光線と反射光線に下した垂線の足をそれぞれB ,Aとおく.
上図の点線部分のように,同一波面上の反射波の位相(または,入射波の位相)は同じである.
このことから,Pにおける入射波の変位$y_{1}$はBにおける入射波の変位と等しく,Pにおけるにおける反射波の変位$y_{2}$はAにおける反射波の変位と等しい.
以上のことを利用して,Pにおける波の式$y_{1}+y_{2}$を計算し,積の形にすることで,隣り合う腹線の間隔を求めよ.

Pの入射波の位相はBの位相と同じであること,反射波の位相はAであることを用いていましょう.
さきほどの補題で,OB間の距離とOA間の距離を求めたので,ざっくりと図をかくと,次のようになります.
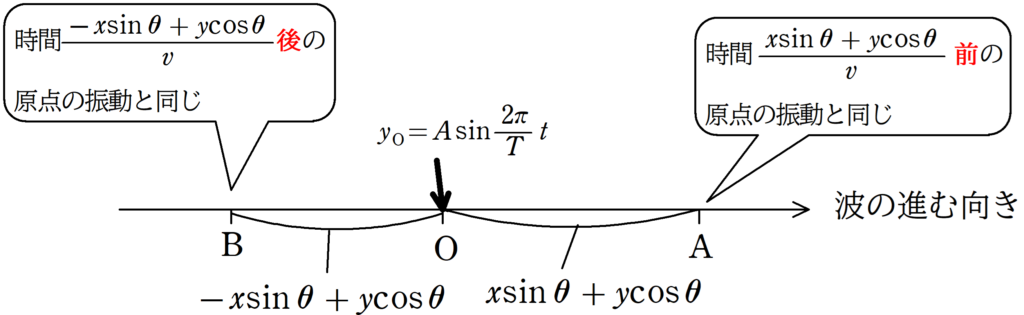

波の進む向きはB→O→Aであって,Oの入射波の媒質の振動がわかっています.
Bでの振動は時間$\dfrac{-x\sin\theta +y\cos\theta}{v}$後の原点Oでの振動と同じで,Aでの振動は,時間$\dfrac{x\sin\theta +y\cos\theta}{v}$前の原点Oでの振動と同じです.

波の式の立て方は,こちらで解説しているので,参考にしてください.
★ Bについて,時刻$t$における入射波の式$y_{1}$
$y_{1}=A\sin\dfrac{2\pi}{T}(t+\dfrac{-x\sin\theta +y\cos\theta}{v})$ $\dots (\ast)$
★ Aについて,時刻$t$における反射波の式$y_{2}$
$y_{2}=A\sin\dfrac{2\pi}{T}(t-\dfrac{x\sin\theta +y\cos\theta}{v})$ $\dots (2\ast)$
★ Pでの波の式
$(\ast) , (2\ast)$より,Pでの合成波の変位$y_{\rm P}$は
$\eqalign{y_{\rm P}&=y_{1}+y_{2}\\&=A\sin\dfrac{2\pi}{T}(t+\dfrac{-x\sin\theta +y\cos\theta}{v})+A\sin\dfrac{2\pi}{T}(t-\dfrac{x\sin\theta +y\cos\theta}{v})\\&=2A\sin\dfrac{2\pi}{T}(t-\dfrac{x\sin\theta}{v})\cos\dfrac{2\pi}{T}\dfrac{y\cos\theta}{v} \dots (3\ast)}$

上では,和→積の変換式を使ったよ.

三角関数の和→積の変換式(その逆の積→和も同様)は,覚えるのが大変なので,導出方法を知っておくとよいでしょう.
★ $\sin +\sin$について
1. $\sin$の加法定理を書き出す.
$\sin(\alpha +\beta)=\sin\alpha\cos\beta +\cos\alpha\sin\beta$ $\dots (\ast)$
$\sin(\alpha -\beta)=\sin\alpha\cos\beta -\cos\alpha\sin\beta$ $\dots (2\ast)$
2. $(\ast)+(2\ast)$を計算する.
$\sin(\alpha +\beta)+\sin(\alpha -\beta)=2\sin\alpha\cos\beta$ $\dots (3\ast)$
3. $A=\alpha +\beta$,$B=\alpha -\beta$とする.
$A+B=2\alpha$ $\therefore \alpha=\dfrac{A+B}{2}$ $\dots (\clubsuit)$
$A-B=2\beta$ $\therefore \beta=\dfrac{A-B}{2}$ $\dots (\spadesuit)$
4. $(\clubsuit),(\spadesuit)$を$(3\ast)$に代入
$\sin A+\sin B=2\sin\dfrac{A+B}{2}\cos\dfrac{A-B}{2}$
★ $\cos -\cos$について
1. $\cos$の加法定理を書き出す.
$\cos(\alpha +\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$ $\dots (\ast)$
$\cos(\alpha -\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$ $\dots (2\ast)$
2. $(\ast)+(2\ast)$を計算する.
$\cos(\alpha +\beta)+\cos(\alpha -\beta)=2\cos\alpha\cos\beta$ $\dots (3\ast)$
3. $A=\alpha +\beta$,$B=\alpha -\beta$
$A+B=2\alpha$ $\therefore \alpha=\dfrac{A+B}{2}$ $\dots (\clubsuit)$
$A-B=2\beta$ $\therefore \beta=\dfrac{A-B}{2}$ $\dots (\spadesuit)$
4. $(\clubsuit),(\spadesuit)$を$(3\ast)$に代入
$\cos A+\cos B=2\cos\dfrac{A+B}{2}\cos\dfrac{A-B}{2}$

また,波の基本式
$v=\dfrac{\lambda}{T}$
より
$\lambda =vT$を利用して$(3\ast)$を変形すると次のようになります.
$y_{\rm P}=$$2A\cos\{\dfrac{2\pi y\cos\theta}{\lambda}\}$$\sin\dfrac{2\pi}{T}(t-\dfrac{x\sin\theta}{v})$

上式の緑部分が時間によって変化する振動部分で,青い部分の絶対値が振幅に相当します.
振幅が最大となるのは
$|\cos\dfrac{2\pi y\cos\theta}{\lambda}|=1$
のときです.
$|\cos\dfrac{2\pi y\cos\theta}{\lambda}|=1$より,自然数$m$を用いて
$\dfrac{2\pi y\cos\theta}{\lambda}=m\pi$
$\therefore y=\dfrac{m\lambda}{2\cos\theta}$
具体的には
$y=\dfrac{1}{2\cos\theta}\lambda, \dfrac{2}{2\cos\theta}\lambda , \dots$
つまり,腹線と腹線の距離は
$\dfrac{2}{2\cos\theta}\lambda -\dfrac{1}{2\cos\theta}\lambda=$$\dfrac{\lambda}{2\cos\theta}$

これは
で解いた答えと一致するね!



コメント