
質量$m$と質量$M$の物体の衝突を重心からみるとどのようになるのかを説明します.
結論を言うと,次のようになります.
重心からみた衝突直後の速度は衝突直前の速度の$-(反発係数)$倍になる.

次の図のように,衝突前の質量$m,M$の速度を$v,V$とし,衝突後の速度を$v’,V’$とします.
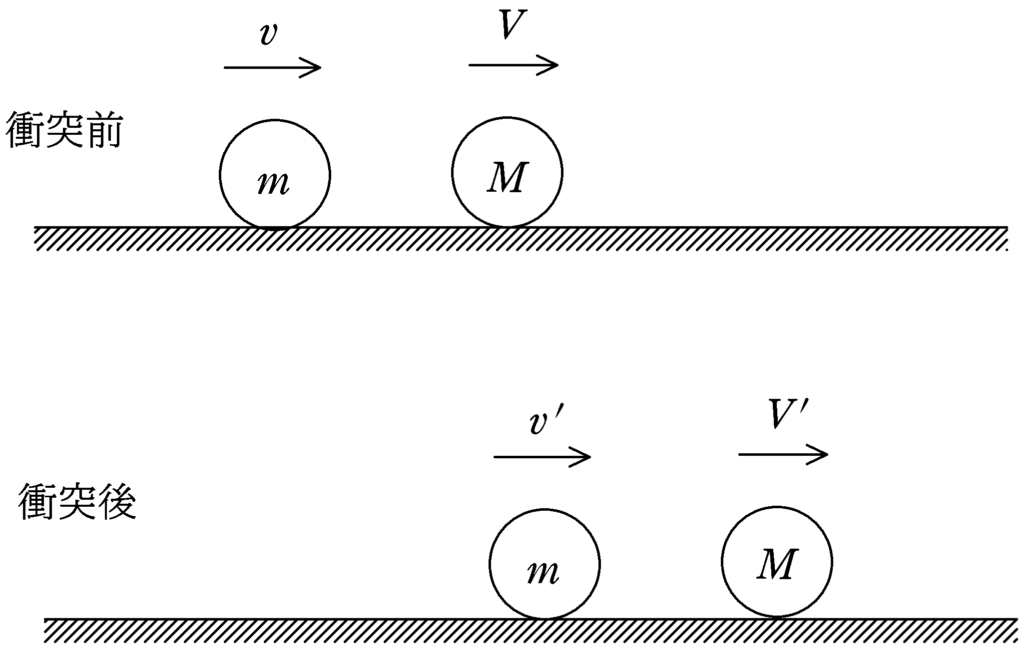

次の2つの式を立てていきます.
- はねかえり(反発)係数の式
- 衝突後の重心からみた運動量の和が$0$の式(下の記事で説明があります.)
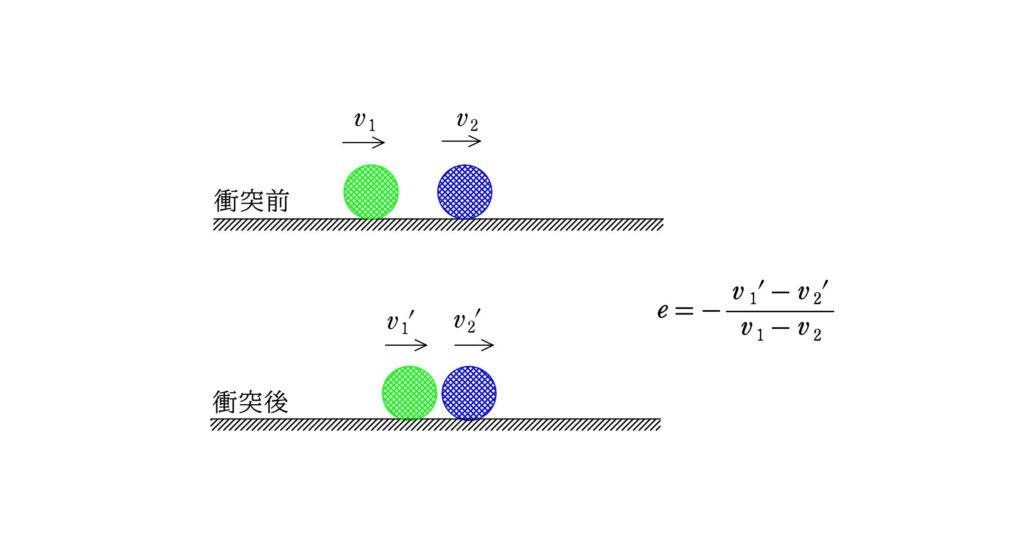
衝突前の物体の速度を$v_{1}$,$v_{2}$,衝突後の速度を$v_{1}^{\prime}$,$v_{2}^{\prime}$とするとき,はねかえり係数(反発係数)の式を次のように定義する.
$e=-\dfrac{v_{1}^{\prime}-v_{2}^{\prime}}{v_{1}-v_{2}}$
$e=1$のときを弾性衝突といい,力学的エネルギーが保存する.
また,$e=0$のときを完全非弾性衝突という.
★ 反発係数の式
$e=-\dfrac{v’-V}{v-V}$ $\therefore\,\, v’-V’=-e(v-V)$ $\cdots (\ast)$
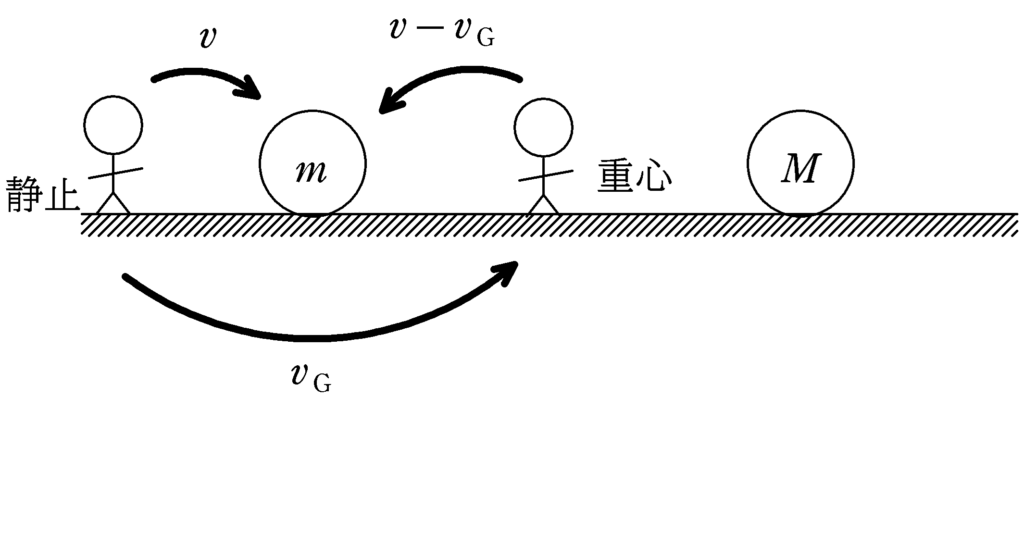

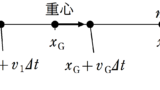
重心速度を$v_{\rm G}$としましょう.衝突をする際,力の和が$0$のため,重心速度は衝突前後で変化しません.
衝突前の重心からみた質量$m$の速度は$v-v_{\rm G}$,質量$M$の速度は$V-v_{\rm G}$.衝突後の重心からみた質量$m$の速度は$v’-v_{\rm G}$,質量$M$の速度は$V’-v_{\rm G}$となります.
重心からみた運動量の和は常に$0$なので次の式を立てることができます.
★ 重心からみた運動量の和が$0$の式
$m(v-v_{\rm G})+M(V-v_{\rm G})=m(v’-v_{\rm G})+M(V’-v_{\rm G})=0$ $\cdots (2\ast)$

$(\ast)$の式から,無理やり$v-v_{\rm G},V-v_{\rm G},v’-v_{\rm G},V’-v_{\rm G}$をつくってみます.
★ $(\ast)$の式の変形
$v’-v_{\rm G}+v_{\rm G}-V’=-e(v-v_{\rm G}+v_{\rm G}-V)$
$\therefore\,\, v’-v_{\rm G}-(V’-v_{\rm G})=-e\left\{v-v_{\rm G}-(V-v_{\rm G})\right\} \cdots (3\ast)$

みやすくするために,重心からみた速度を$v-v_{\rm G}=v_{\rm G1},V-v_{\rm G}=V_{\rm G2},v’-v_{\rm G}=v’_{\rm G1},V’-v_{\rm G}=V’_{\rm G2}$とおきます.
★ おきかえ
$(2\ast)$
$mv_{\rm G1}+MV_{\rm G2}=0 \cdots (\sharp)$ かつ $mv’_{\rm G1}+MV’_{\rm G2}=0 \cdots (2\sharp)$
$(3\ast)$
$v’_{\rm G1}-V’_{\rm G2}=-e(v_{\rm G1}-V_{\rm G2}) \cdots (3\sharp)$

$(\sharp)$より,$V_{\rm G2}=-\dfrac{m}{M}v_{\rm G1}$,$(2\sharp)$より,$V’_{\rm G2}=-\dfrac{m}{M}v’_{\rm G1}$と変形して,$3(\sharp)$に代入し,整理していきます.
★ $(\sharp),(2\sharp)$を$(3\sharp)$に代入
$\eqalign{v’_{\rm G1}+\dfrac{m}{M}v’_{\rm G1}&=-e\left(v_{\rm G1}+\dfrac{m}{M}v_{\rm G1}\right)\\\cancel{\dfrac{M+m}{M}}v’_{\rm G1}&=-e\times \cancel{\dfrac{M+m}{M}}v_{\rm G1}\\v’_{\rm G1}&=-ev_{\rm G1}}$

たしかに$-e$倍になったね.
ちなみにこの事実は覚えておいた方がいいの?

大学入試の問題を解くうえでは覚えておかないと解けないという問題はでないはずです.
ただ,反発係数の式や運動量保存則,重心からみた運動量の和が$0$になる式は立てられるようにしておくとよいです.
ちなみに,同じように計算すれば,$V’_{\rm G2}=-eV_{\rm G2}$も導出できます.
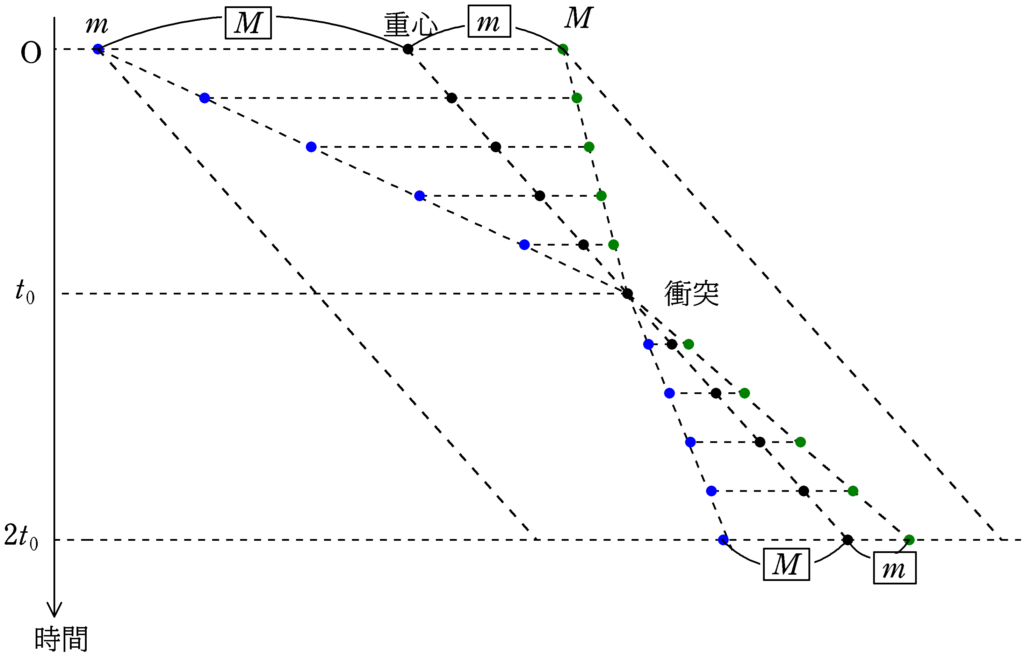
最後に等速直線運動をする2つの物体の衝突前後の位置の時間変化の図をみてみましょう.
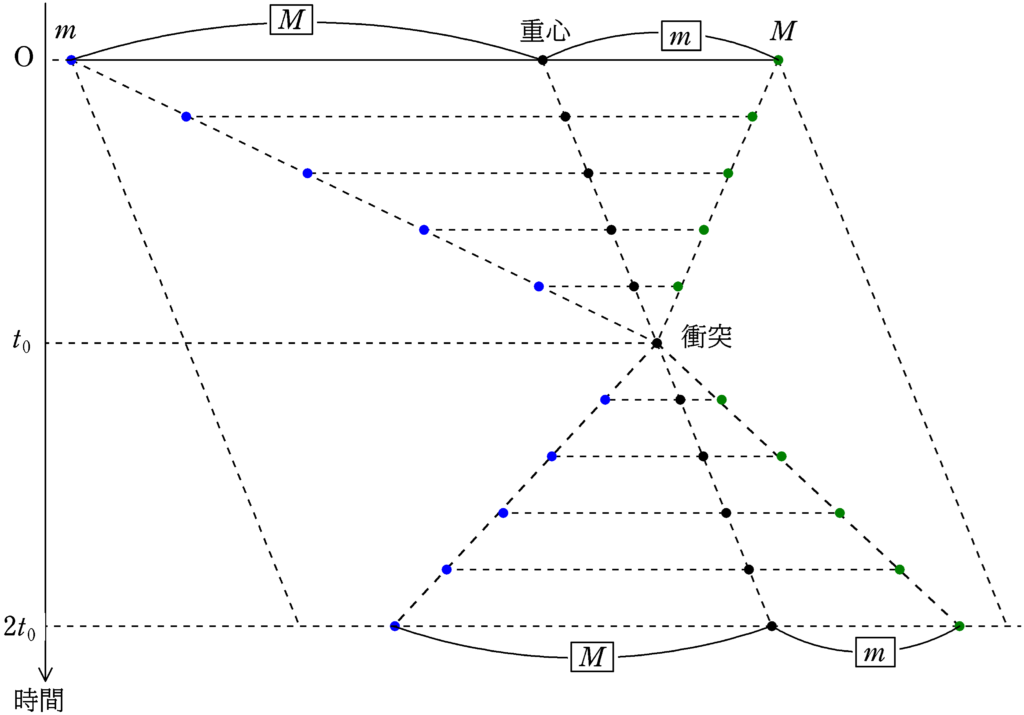

重心は速度が一定なので,一定時間に一定距離動きます.また,重心は質量$m$と質量$M$の物体のいる位置を常に$M:m$に内分する点にあります.(これは衝突後も同じ.)
上の図では,反発係数を$\dfrac{4}{5}$で描いてみました.
たとえば,質量$m$の物体(青の点)に着目すると,同じ時間$t_{0}$で質量$m$の物体は$\dfrac{4}{5}$倍の距離しか移動しません.

また,ご存じの通り,衝突をしたからといって質量$m$の物体は必ず左方向にいくわけではありません.
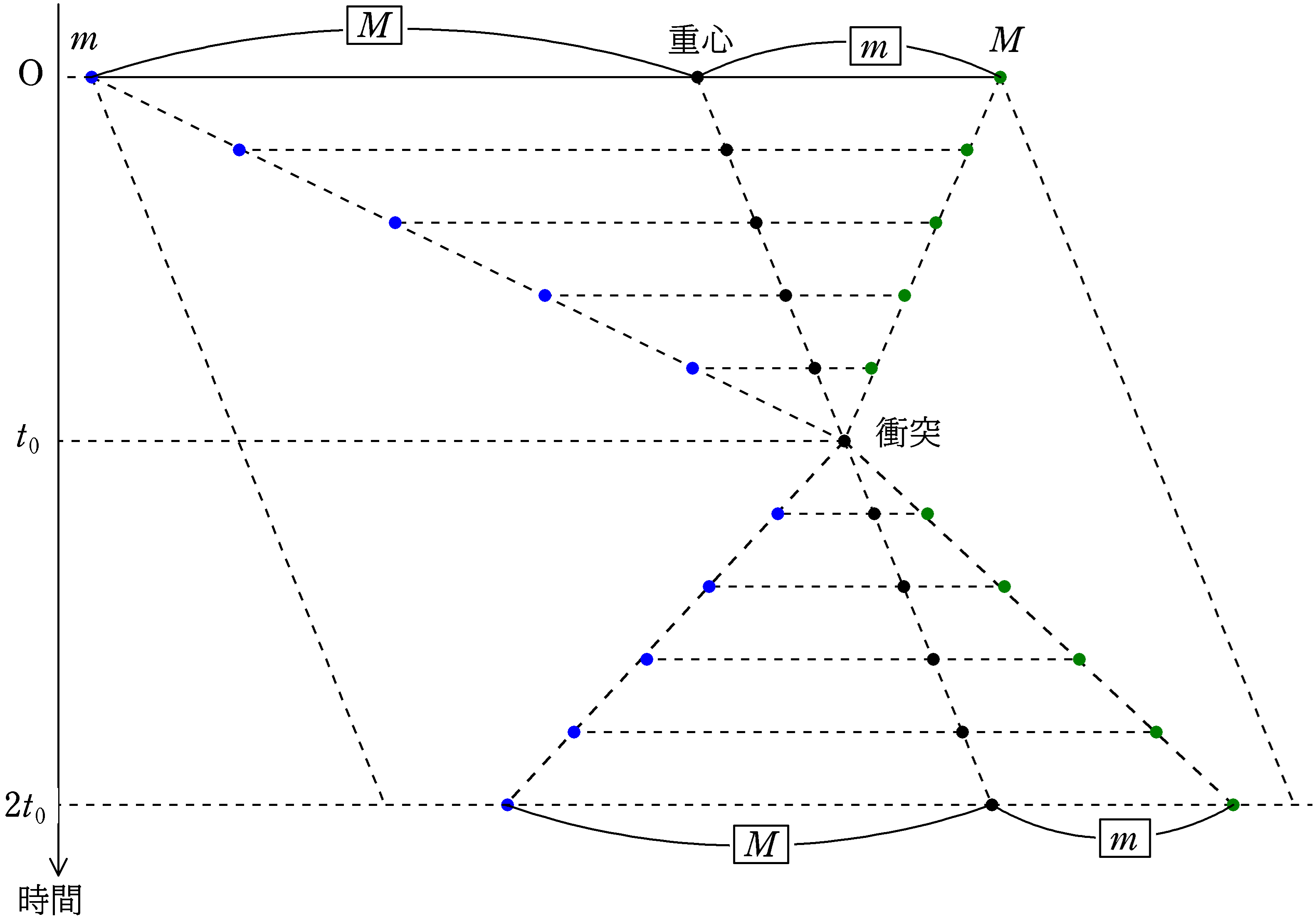
下図は,質量$m$の物体が衝突後右の速度を持ち続ける図です.

コメント